Multi-Gigahertz-Taktbäume
Neun Tipps zum Minimieren von Laufzeitabweichungen
Laufzeitunterschiede in der Taktverteilung eines Geräts oder Systems können viele Ursachen haben. Sie zu kompensieren erfordert Know-how und ist mit Aufwand verbunden.
Es ist nicht ungewöhnlich, dass Taktsignale in umfangreichen Systemen mehrere Taktbausteine, unterschiedliche Arten von Übertragungsleitungen und zahlreiche Leiterplatten und Koaxialkabel durchlaufen. Selbst wenn Ingenieure sich genau an die bewährten Regeln der Technik halten, kann jedes dieser Medien einen Taktversatz (clock skew) von mehr als 10 ps verursachen. In vielen Anwendungen ist es jedoch wünschenswert, dass alle Taktsignale einen Versatz von weniger als 1 ps aufweisen. Beispiele für solche Applikationen sind phasengesteuerte Gruppenantennen (Phased-Array), MIMO-Anwendungen, Radarsysteme, elektronische Kampfführung, Bilderfassung mit Millimeterwellen, Messgeräte und Software Defined Radio (SDR).
Jobangebote+ passend zum Thema
Laufzeitgleichungen für Übertragungsleitungen
Mit den folgenden Gleichungen lässt sich die Signallaufzeit tS für einen Taktpfad sowie der Laufzeitunterschied (ΔtS) für verschiedene Taktpfade oder Änderungen der Umgebungsbedingungen abschätzen. In einem großen Taktverteilsystem trägt der Laufzeitunterschied ΔtS für die verschiedenen Takt-Leiterbahnen einen Teil zum Taktversatz des Gesamtsystems bei. In den Gleichungen 1 und 2 kommen zwei Hauptvariablen vor, die den tS-Wert einer Übertragungsleitung beeinflussen. Dies sind die mechanische Länge (l) und die effektive relative Dielektrizitätszahl (εr eff) einer Übertragungsleitung.
In beiden Gleichungen ist vP die Phasengeschwindigkeit der Übertragungsleitung, VKF der Verkürzungsfaktor in Prozent und c die Lichtgeschwindigkeit (299.792.458 m/s).
Gleichung 3 dient zur Berechnung der Laufzeitdifferenz (ΔtS) zwischen Übertragungsleitungen.
Die Eigenschaften der dielektrischen Materialien von Übertragungsleitungen ändern sich mit der Temperatur. Der Temperaturkoeffizient der Dielektrizitätszahl (TKε) wird oft als Diagramm geliefert, das die Phasenänderung (Δφppm) in ppm (parts per million) als Funktion der Temperatur angibt. Der Δφppm-Wert gibt die Phasenabweichung bei einem Temperaturwert gegenüber der Phase bei einer Referenztemperatur (üblicherweise 25 °C) an. Für eine gegebene Temperatur, einen bestimmten Δφppm-Wert und eine gegebene Leitungslänge ermöglicht Gleichung 4 ein Abschätzen der Änderung der Signallaufzeit gegenüber jener bei der Referenztemperatur.
Die Dielektrika von Koaxialkabeln haben Eigenschaften, die sich je nach Biegung des Kabels verändern. Der Radius und der Winkel der Kabelbiegung entscheiden über die Veränderung der effektiven Dielektrizitätszahl. In der Regel wird dies als Phasenänderung (Δφ) angegeben, die bei einer gegebenen Kabelbiegung gegenüber einem geraden Kabel entsteht. Wenn der Wert für die Phasenänderung durch Biegung (Δφ), die Signalfrequenz (f) und die Kabelbiegung bekannt sind, lässt sich mit Gleichung 5 berechnen, wie sich die Signallaufzeit ändert.
Auswahl der Übertragungsleitung
Unterschiedliche Arten von Übertragungsleitungen ergeben verschiedene εr eff- und vP-Werte. Gemäß Gleichung 2 bedeutet dies, dass gleich lange Übertragungsleitungen unterschiedlichen Typs verschiedene tS-Werte aufweisen.
Tabelle 1 enthält die Simulationsergebnisse dreier gängiger Arten von Übertragungsleitungen (Koplanar-, Mikrostreifen- und Streifenleitung) und zeigt die Unterschiede in Sachen εr eff, vP und tS. Laut dieser Simulation ist die geschätzte Signallaufzeit (tS) einer 10 cm langen Koplanarleitung um 100 ps kleiner als diejenige einer gleich langen Streifenleitung. Die Simulationen wurden mithilfe des Microwave Impedance Calculators der Rogers Corporation durchgeführt.
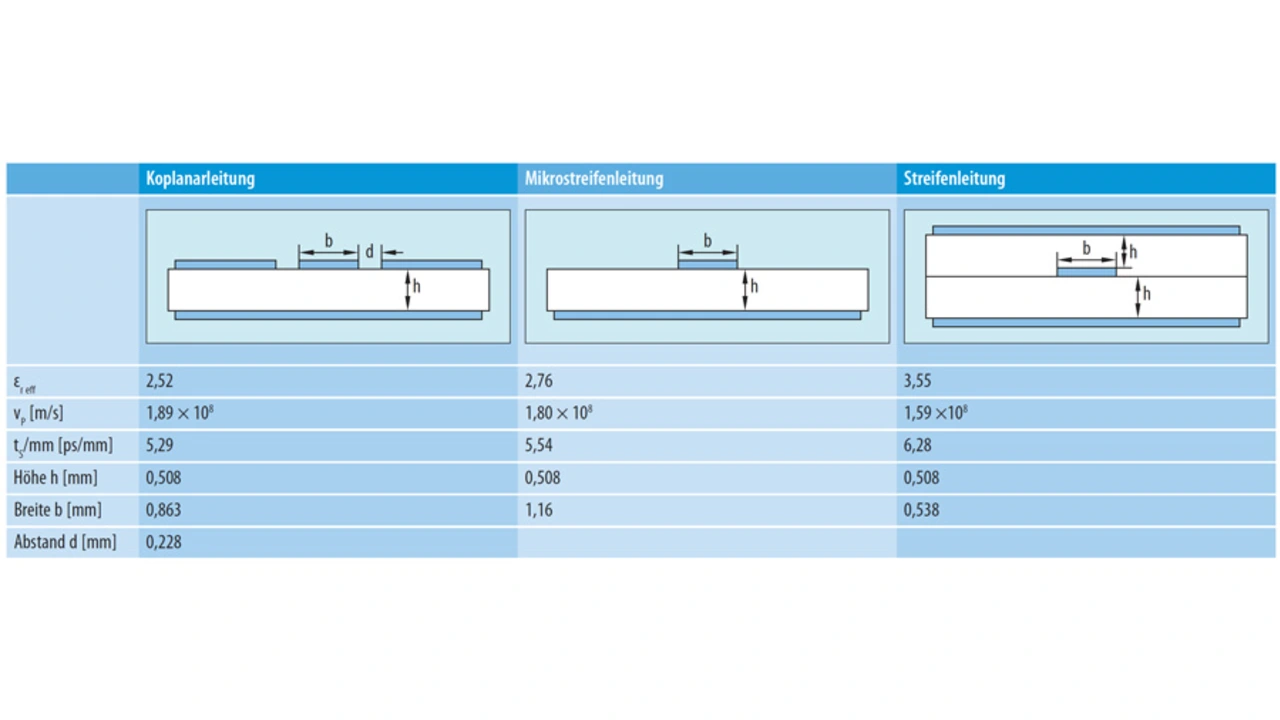
Es ist nicht immer möglich, alle laufzeitangepassten Signale auf derselben Leiterplattenlage zu verlegen oder über denselben Leitungstyp zu führen.
In Tabelle 2 sind einige generalisierte Überlegungen zur Auswahl des Leitungstyps für unterschiedliche Leiterbahnen aufgeführt. Wenn es notwendig ist, die Signallauf-zeitwerte verschiedener Leitungstypen aneinander anzupassen, eignet sich ein Leiterplatten-Simulationstool besser als manuelle Berechnungen und Faustregeln.
Leitungen mit Durchkontaktierungen
Für eine grobe Berechnung der Signallaufzeit kann angenommen werden, dass die Länge der Durchkontaktierung zwischen den beiden Signallagen die gleiche Phasengeschwindigkeit wie die Leitung aufweist. Demnach würde also eine Durchkontaktierung zwischen der obersten und der untersten Signallage einer 1,5 mm dicken Leiterplatte eine zusätzliche Signallaufzeit von rund 10 ps bewirken.
Dichte Leiterbahnen, differenzielle und massebezogene Signale
Die Signalrichtung dicht gepackter, benachbarter Leiterbahnen verändert den εr eff-Wert und beeinflusst deshalb auch die Laufzeitanpassung zwischen gleich langen Leiterbahnen. Eine Simulation von zwei seitengekoppelten Mikrostreifenleitungen im Vergleich zu einer einzelnen Mikrostreifenleitung zeigt Tabelle 3.
Diese Simulation verdeutlicht, dass die Signallaufzeit (tS) von zwei 10 cm langen seitengekoppelten Leiterbahnen mit phasengleichen, massebezogenen Signalen (even mode) um 16 ps größer ist als diejenige einer gleich langen einzelnen Leiterbahn.
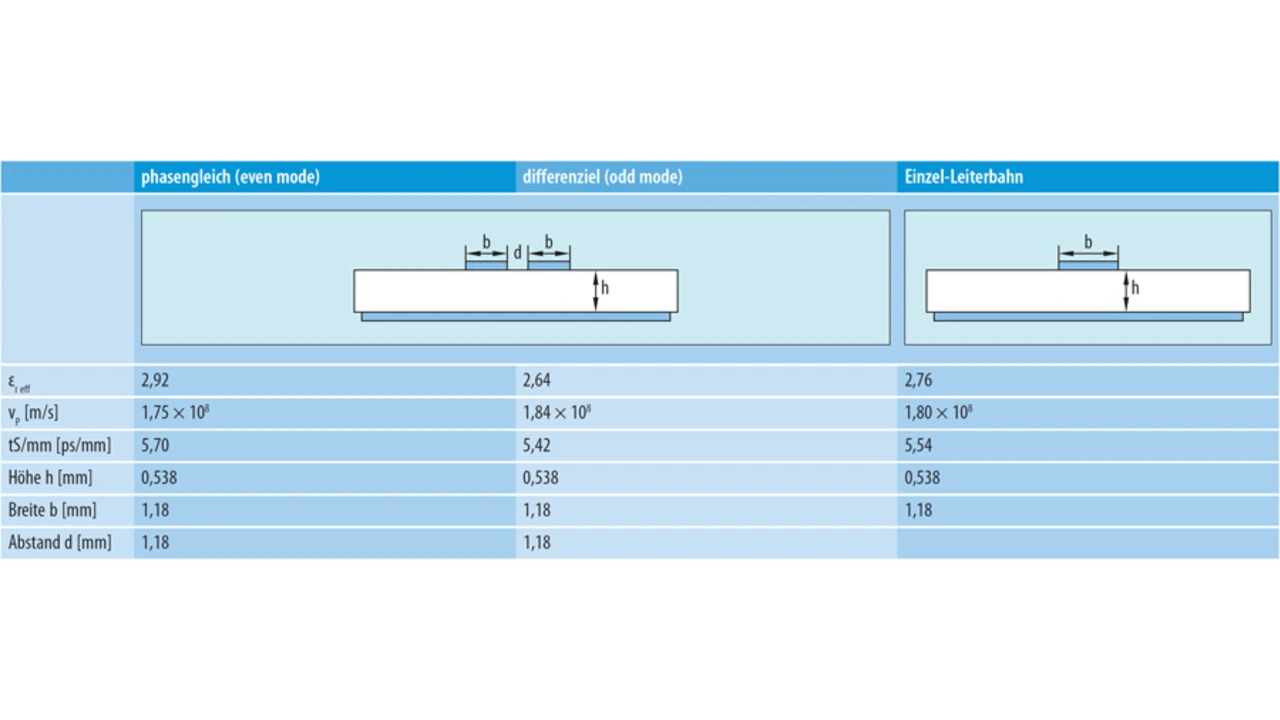
Beim Versuch der Anpassung von massebezogenen und differenziellen Signallaufzeiten kommt es darauf an, die Phasengeschwindigkeiten beider Signalpfade zu simulieren. In Taktschaltungen kann diese Situation beim Versuch zum Senden eines CMOS-Sync- oder SYSREF-Anforderungssignals vorkommen, das zeitlich an einem differenziellen Referenz- oder Taktsignal ausgerichtet ist.
Wird der Abstand zwischen den differenziellen Signalpfaden vergrößert, so lässt sich eine bessere Anpassung der Phasengeschwindigkeit zwischen den differenziellen und den massebezogenen Signalen erreichen. Dies geht allerdings zu Lasten der Gleichtaktunterdrückung des differenziellen Signals, die den Taktjitter auf ein Minimum begrenzt.
Für das Layout einer Leiterplatte ist außerdem zu beachten, dass dicht gepackte phasengleiche Signale (even mode) den εr eff-Wert erhöhen und sich deshalb größere Signallaufzeiten (tS) ergeben. Hierzu kommt es z. B. wenn mehrere Kopien massebezogener Signale in engem Abstand zueinander verlaufen.
9 Tipps gegen Laufzeitabweichungen
- Neun Tipps zum Minimieren von Laufzeitabweichungen
- Laufzeit als Funktion der Frequenz
- Laufzeitangepasste Kabel
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Car-Camera-Bus-Technologie (C2B)
Fahrzeug-Kamera-Verbindung
Systemdesign / Safety&Security
Funktionale Sicherheit in der Datenerfassung
