Digitale Filter für Delta-Sigma-Wandler
Siebe aus Silizium
Fortsetzung des Artikels von Teil 1
Digitale FIR-Filter
Wenn ein System einen breiten und nicht vorhersehbaren Bereich von Frequenzen erzeugt (z.B. bei seismischen Anwendungen oder Vibrationsanalysen), empfiehlt sich stattdessen die Verwendung eines A/D-Wandlers mit anderen digitalen Filtern. Die Delta-Sigma-A/D-Wandler ADS1281 und ADS1282 sind für derartige Applikationen konzipiert, in denen ein breites Eingangsspektrum vorliegt und sichergestellt sein muss, dass jegliche Frequenzanteile oberhalb der Nyquist-Frequenz wirkungsvoll abgeschwächt werden.
Jobangebote+ passend zum Thema
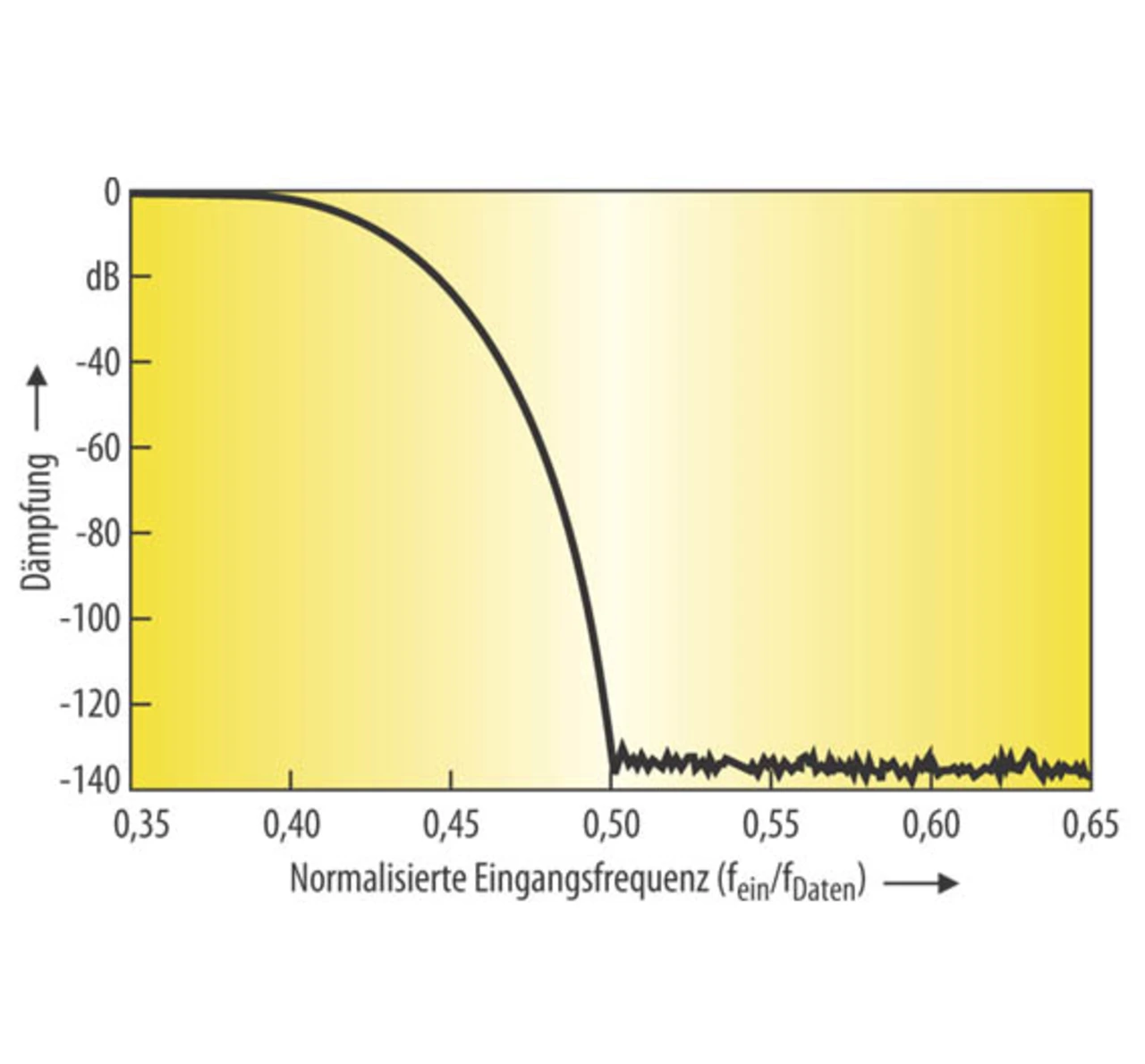
Bild 3 zeigt den Frequenzgang des FIR-Filters im ADS1281. Die Dämpfung bei der Nyquist-Frequenz beträgt 130 dB. Die gezeigte Filterkennlinie ist normiert und skaliert mit der Datenrate. Das bedeutet, dass die Kennlinie des FIR-Filters unverändert bleibt, wenn die Ausgangs-Datenrate zwischen 250 S/s und 4 kS/s variiert wird. Beim Design des analogen Anti-Alias-Filters muss deshalb nur die Nyquist-Frequenz des Modulators beachtet werden.
Der Frequenzgang des FIR-Filters im normierten Durchlassband von 0 bis 0,375 von Bild 3 hat einen flachen Verlauf mit einer Welligkeit von nur ±0,003 dB. Besteht das Eingangssignal aus einem breiten Band von Frequenzkomponenten, so wird dieses breite und flache Durchlassband benötigt, um die Amplituden der Frequenzkomponenten nicht zu verfälschen.
Da die Modulator-Abtastrate des ADS1281 und des ADS1282 maximal 1024 MHz beträgt, sollte das analoge Anti-Alias-Filter so eingestellt werden, dass die gewünschte Abschwächung bei 512 kHz einsetzt. Das Filter kann auf einfache Weise mit der FilterPro-Software dimensioniert werden. Diese ermöglicht es, verschiedenen Filtertypen (Butterworth, Bessel usw.) auszuprobieren und mit der Zahl der Polstellen zu experimentieren. Auch ein Assistent speziell für Anti-Alias-Filter ist enthalten. Man gibt Systemparameter wie die Nyquist-Frequenz, die gewünschte Dämpfung bei dieser Frequenz, den Filtertyp und andere Parameter ein und erhält ein Design der jeweiligen Filterstufen.
Allerdings geht FilterPro von idealen Operationsverstärkern aus, so dass sich in der Praxis teils große Abweichungen von der idealisierten Kennlinie ergeben können [1]. Es empfiehlt sich deshalb, das Filter nach dem Design mit FilterPro mithilfe von TINA-TI auf der Basis des jeweils gewählten OpAmps zu simulieren.
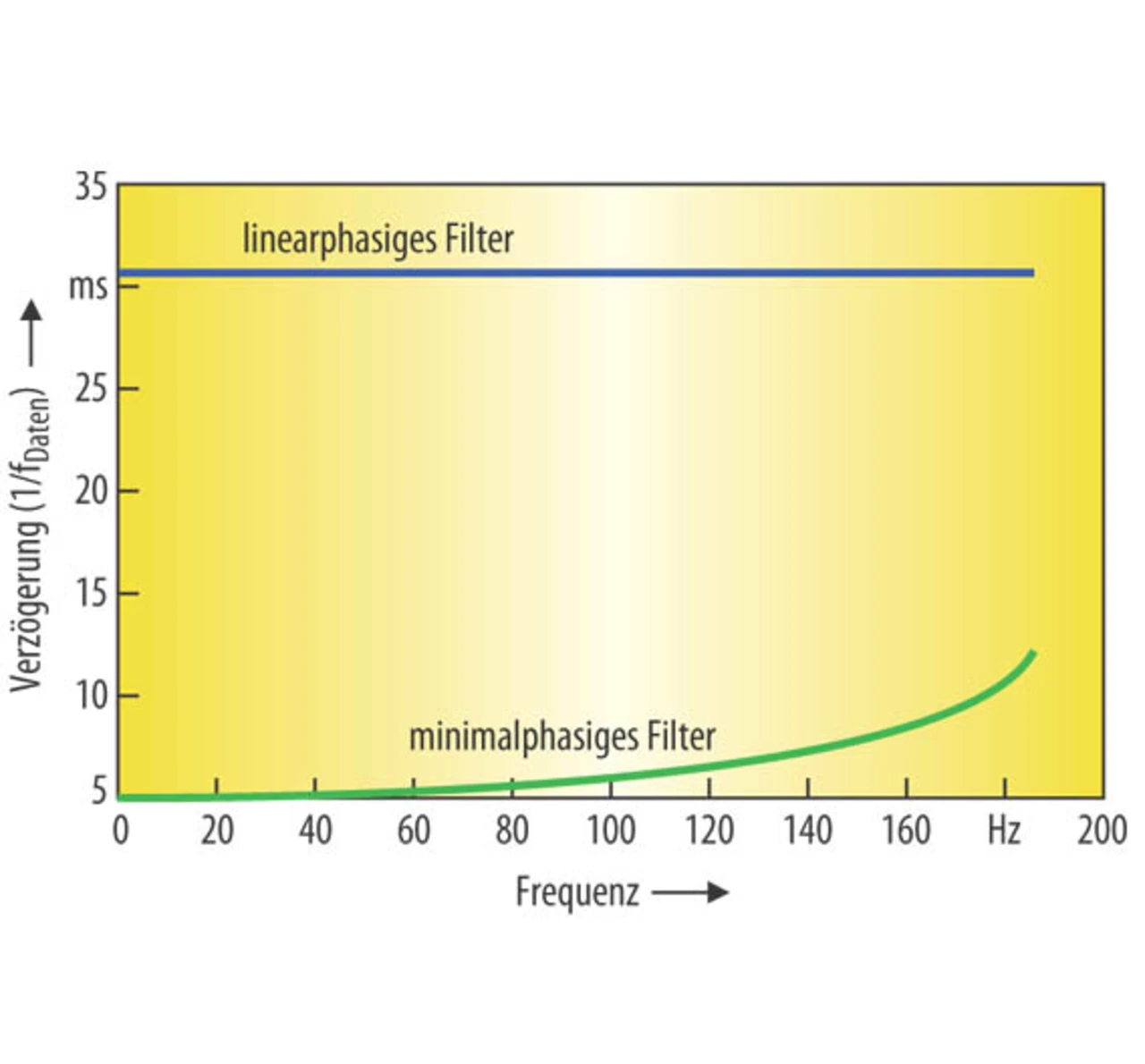
Ein weiterer wichtiger Aspekt dieser FIR-Filter ist ihr Phasengang. Einige Signalquellen sind gegenüber Phasenverzerrungen relativ unempfindlich. Dies gilt unter anderem für Audiosignale. Anders ist es beispielsweise bei seismischen Signalen. Ein ideales Filter dafür hat deshalb einen linearen Phasengang bzw., anders ausgedrückt, eine konstante Gruppenlaufzeit.
Der ADS1281 ermöglicht die Auswahl zwischen dem linearphasigen und dem minimalphasigen Filtertyp (Bild 4). Die Phasenbeziehung eines aus vielen verschiedenen Frequenzen bestehenden Signals bleibt beim Durchlaufen eines phasenlinearen Filters erhalten, da alle Frequenzkomponenten um denselben Betrag verzögert werden - im Falle des ADS1281 um 31 Perioden der Ausgangs-Datenrate.
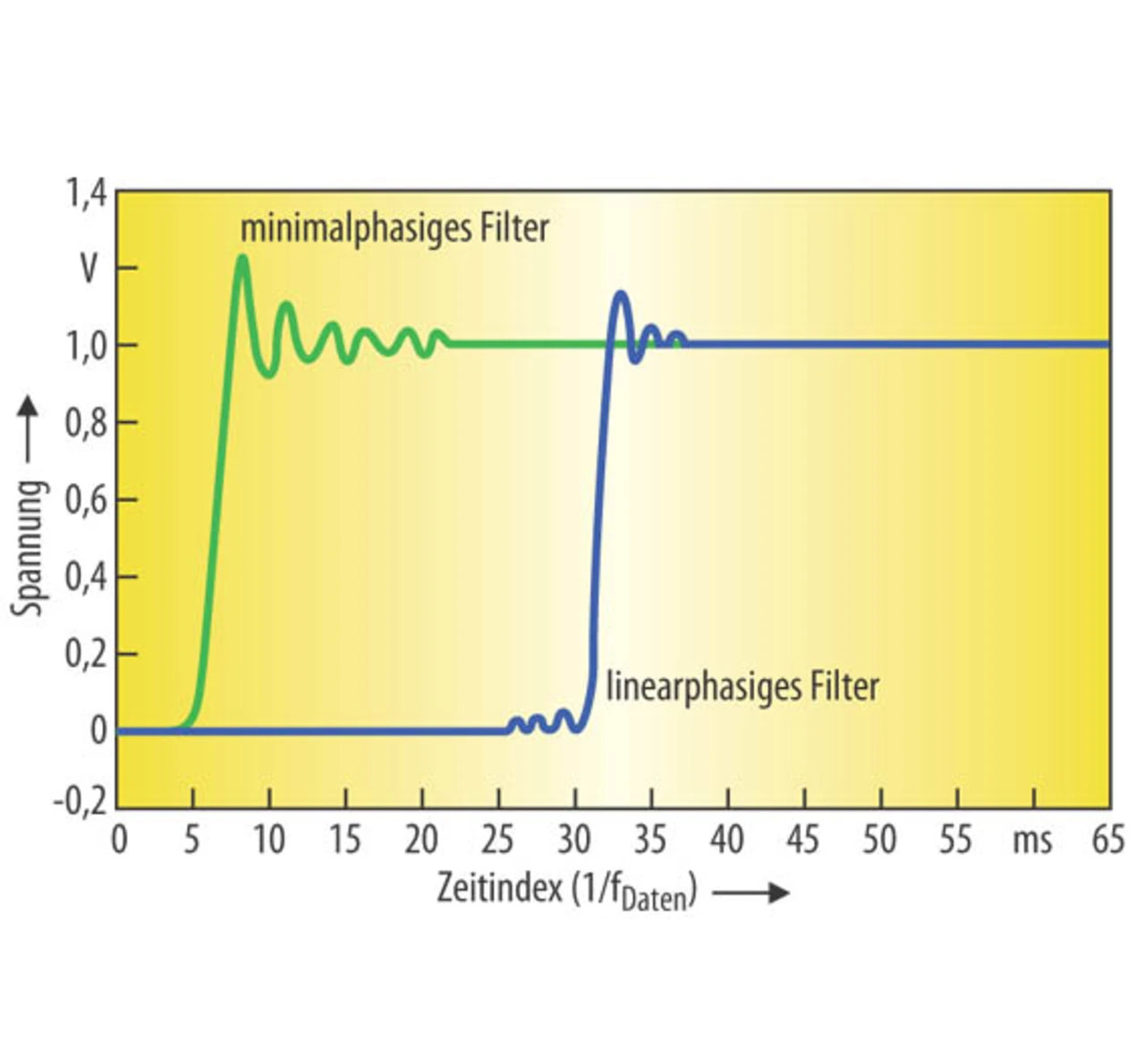
Das linearphasige Filter mit seiner hohen Flankensteilheit ist dabei nicht frei von Nachteilen. Neben der großen Phasenverzögerung gehören dazu das Über- oder Unterschwingen an harten Kanten, zu dem es kommt, wenn die Daten das Filter durchlaufen (Bild 5).
Die Phasenverzögerung ist allerdings konstant, so dass sie in einem realen System, in dem die Datenerfassung durch ein Ereignis angestoßen wird, entsprechend einkalkuliert werden kann.
Den hervorragenden Eigenschaften im Frequenzbereich steht somit eine weniger gute Leistung im Zeitbereich gegenüber, wofür das auch als Gibbssches Phänomen bezeichnete Über- oder Unterschwingen an harten Kanten verantwortlich ist.
- Siebe aus Silizium
- Digitale FIR-Filter
- Weitere Fälle
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Mixed-Signal-ICs
Digitale Features in schnellen D/A-Wandlern
SAR oder ΔΣ?
Welche Datenwandler-Architektur ist die Richtige?
