Auflösung und Genauigkeit
Datenblätter von A/D-Wandlern richtig interpretieren
Fortsetzung des Artikels von Teil 1
Datenblätter von A/D-Wandlern richtig interpretieren
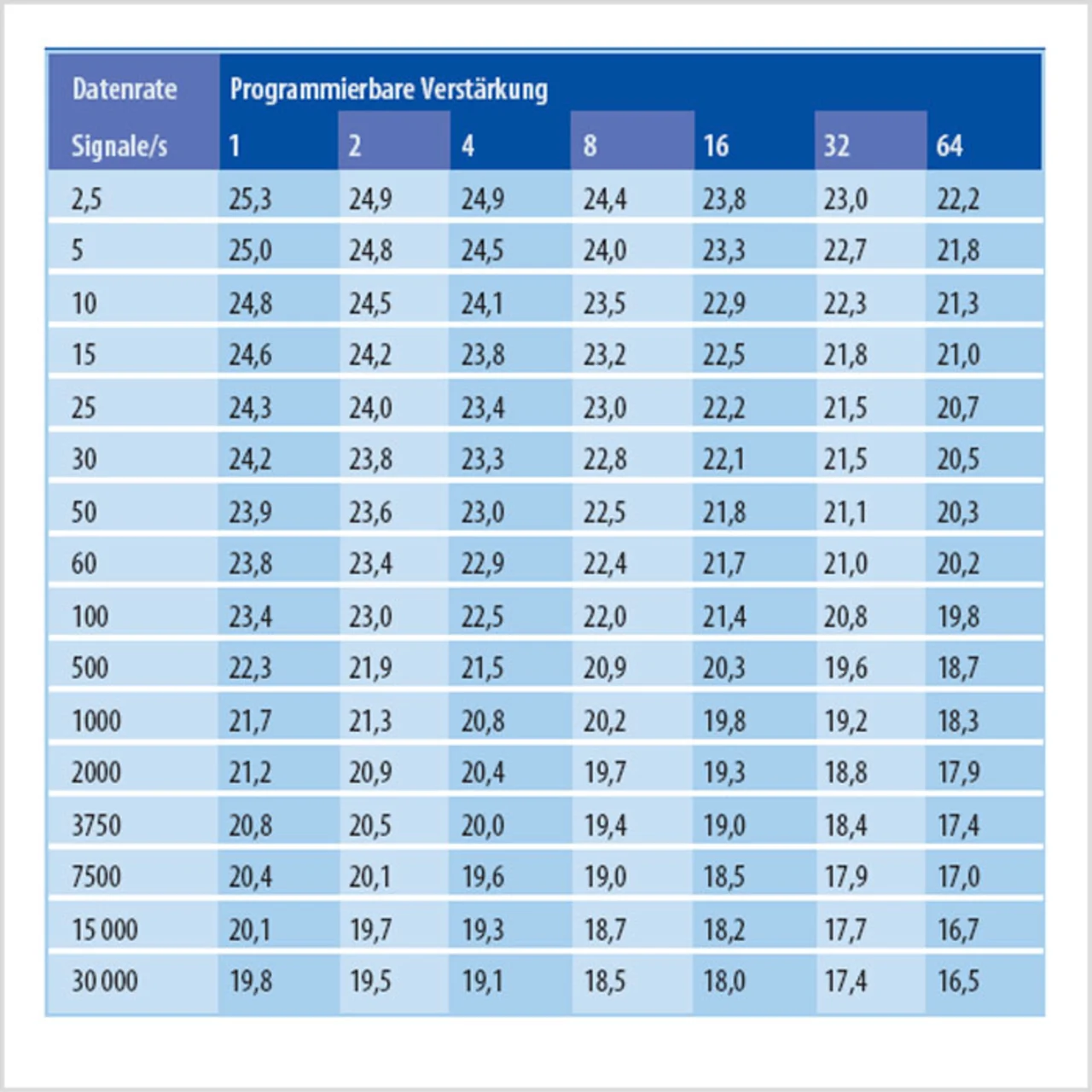
Aus diesem Wert kann man eine effektive Auflösung von 141,2/6,02 = 23,4 bit errechnen. Dies stimmt mit der Zahl in Tabelle 2 für dieselbe Datenrate und programmierbare Verstärkung des PGA überein. Bei Annahme eines Verhältnisses von 6,6 zwischen dem Spitze-Spitze-Wert und dem Effektivwert des Rauschens würde man eine rauschfreie Auflösung von 23,4 – 2,7 = 20,7 bit erwarten.
Tabelle 3 zeigt einen tatsächlichen Wert von 20,9 bit. Die Abweichung zwischen den erwarteten 20,7 bit und den angegebenen 20,9 bit ist darin begründet, dass für diese langsamen Messungen eine kleinere Anzahl von Messwerten verwendet wurde. Bei höheren Datenraten liegt der Unterschied zwischen ENOB und den rauschfreien Bits bei dem erwarteten Wert von 2,7.
Die Berechnungen werden jetzt für dieselbe Datenrate durchgeführt, jedoch wird die PGA-Verstärkung von 1 auf 8 erhöht. Gemäß Tabelle 1 beträgt das eingangsbezogene Rauschen jetzt 0,305 μV. Der Skalenendwert des Eingangs hat sich jedoch von 10 V auf 1,25 V geändert (wegen der Verstärkung von 8). Somit beträgt das SNR:
SNR = 20 × log10 (10/0,305 × 10–6) = 132,3 dB
Die effektive Auflösung beträgt jetzt 132,3/6,02 = 22 bit und die rauschfreie Auflösung 22 – 2,7 = 19,3 bit.
Jobangebote+ passend zum Thema
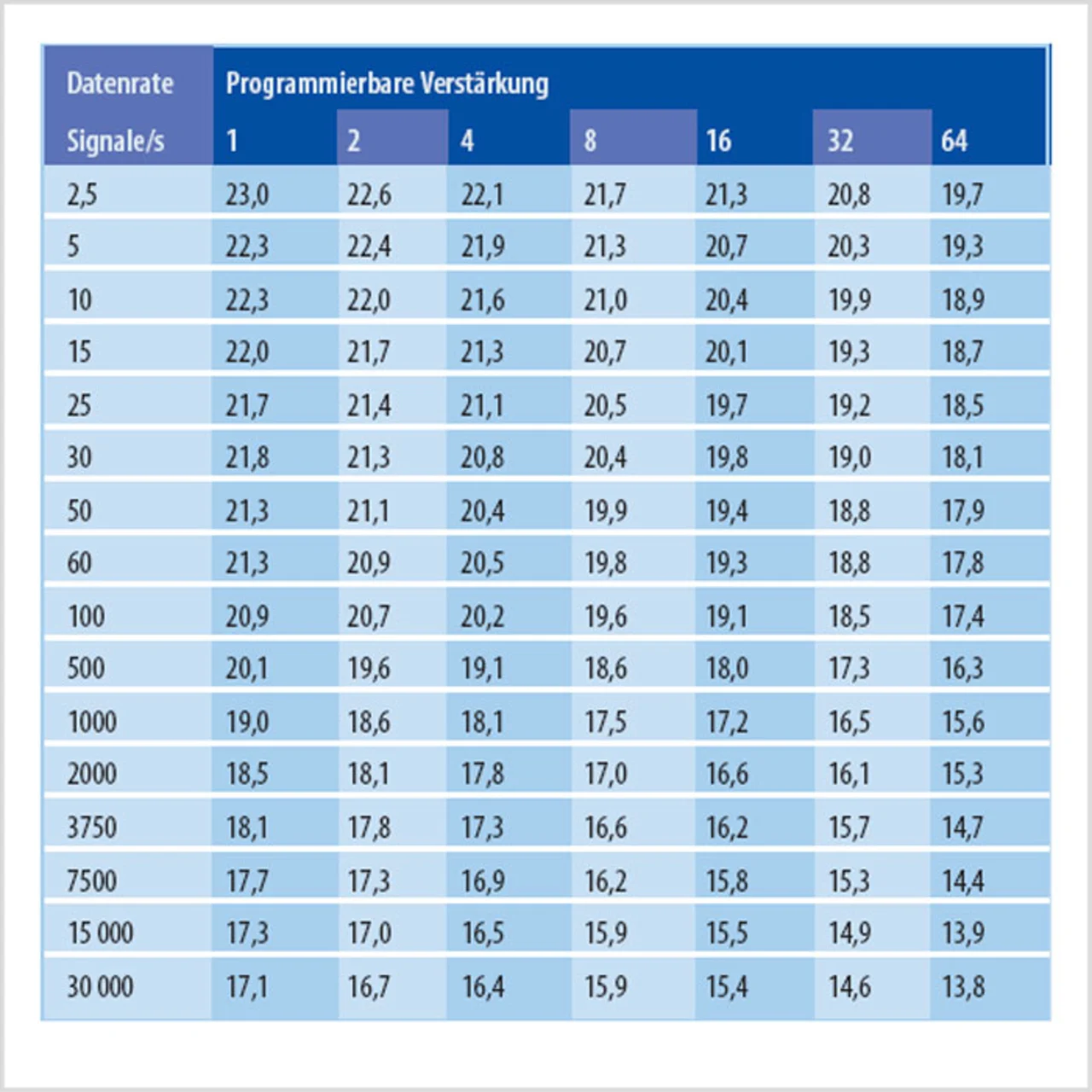
Dies veranschaulicht deutlich die Problematik, wenn von einer Auflösung in bit die Rede ist. Zwischen einer PGAVerstärkung von 1 und einer PGAVerstärkung von 8 sinkt die effektive Auflösung von 23,4 auf 22 bit, was zunächst wie eine Verschlechterung des Rauschverhaltens aussieht. Das eingangsbezogene Rauschen sinkt jedoch von 0,875 μV auf 0,305 μV, was eine Verbesserung des Rauschverhaltens bedeutet. Erklärung: Das eingangsbezogene Rauschen nimmt ab, die Empfindlichkeit des Wandlers und damit die Wertigkeit des LSB ändern sich jedoch um einen größeren Wert. Dies hat mehr rauschende Bits zur Folge, wobei jedes dieser Bits jedoch eine deutlich kleinere Wertigkeit hat, der Wandler also kleinere Signale analysieren kann.
Man könnte zu der Annahme verleitet werden, dass die Auflösung etwas mit der Genauigkeit des ADC zu tun hat. Dies ist nicht der Fall. Wie bereits festgestellt, ist die Auflösung ein Maß für die Reproduzierbarkeit. Ein ADC mit einer hohen Auflösung liefert Ergebnisse mit einer guten Reproduzierbarkeit, könnte jedoch wiederholt das falsche Ergebnis liefern. Seine Auflösung wäre gut, selbst bei geringer Genauigkeit.
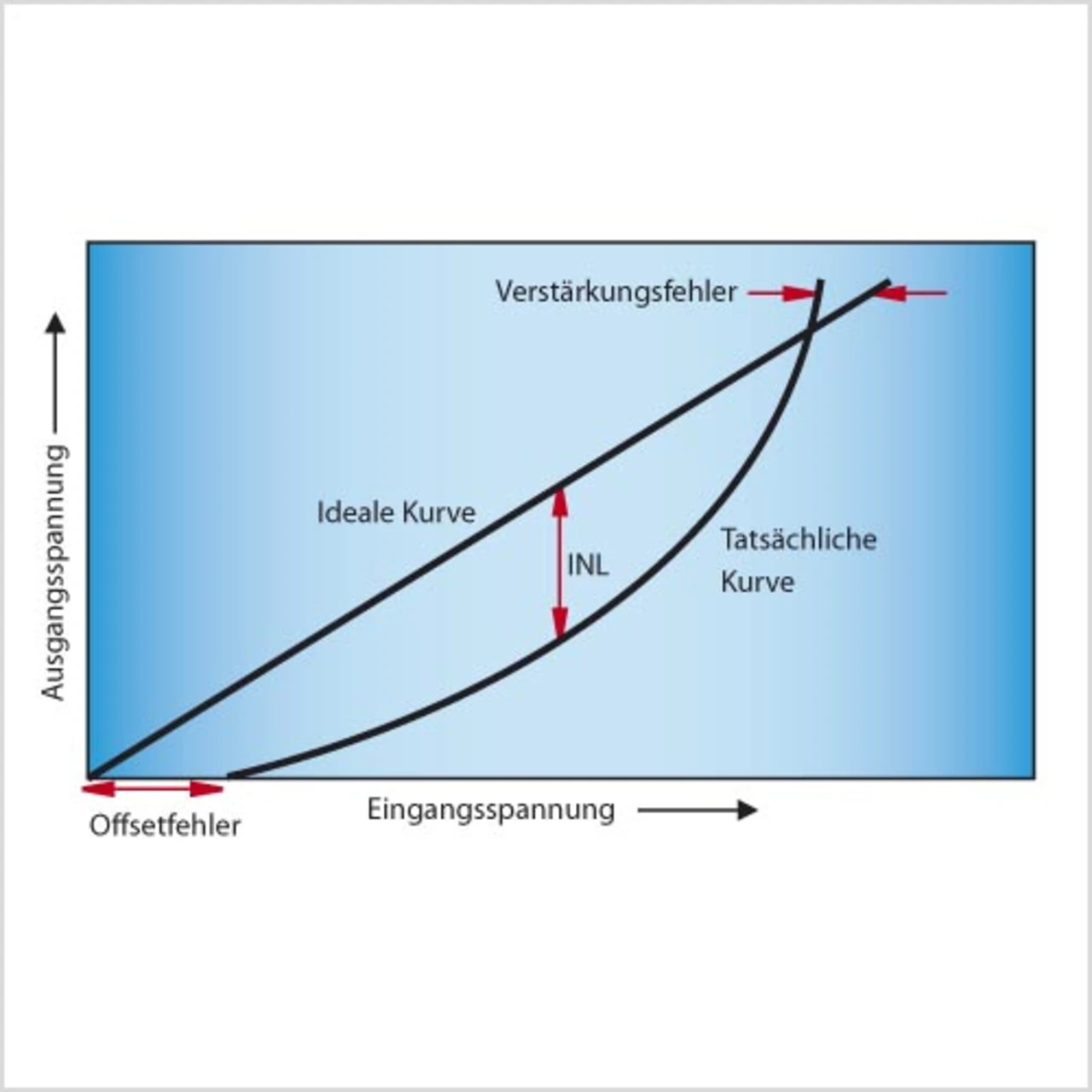
Das Bild zeigt die Übergangseigenschaften bei einem idealen ADC sowie die bei einem realen ADC auftretenden Fehler. Wie zu erkennen ist, gibt es bei einem ADC drei wesentliche Fehlerquellen: den Offset-Fehler, den Verstärkungsfehler und den integralen Linearitätsfehler (INL). Im Zusammenhang mit diesen Fehlern steht auch die Drift über Temperatur und Zeit.
Der beispielhaft herangezogene ADS1252 ist ein 24-bit-Delta-Sigma-ADC mit einer effektiven Auflösung von 19 bit. Die Frage ist: wie hoch ist seine Genauigkeit?
Im Datenblatt ist der Offsetfehler mit ±220 ppm des Skalenendwertes angegeben. Angenommen, der Skalenendwert beträgt 224 Codes, bedeutet dies einen Fehler von 3355 Codes, und da es sich um einen Offset-Fehler handelt, muss dieser Fehler unabhängig von der Signalamplitude auf jeden Messwert angewendet werden. Der Verstärkungsfehler ist mit ±1 % des Skalenendwertes angegeben, was gleichbedeutend mit 167 772 Codes ist. Dieser Wert wird mit der Signalamplitude skaliert, so dass er bei der Hälfte des Skalenendwertes halb so groß ist. Diese Zahlen liefern ganz klar nicht die Genauigkeit, die man erwarten würde, wenn man einfach nur die 19 bit der effektiven Auflösung betrachtet, die in der Überschrift auf der ersten Seite des Datenblatts aufgeführt sind.
All dies wertet den ADS1252 jedoch nicht ab. Dieses Bauteil wurde unter dem Gesichtspunkt guten Wechselstromverhaltens entwickelt und hat eine Gleichstromgenauigkeit, die mit den meisten 16-bit-ADCs vergleichbar ist. Wird eine höhere Genauigkeit gefordert, wäre eine Kalibrierung nötig, um den Offset- und Verstärkungsfehler zu beseitigen. In einigen Bauelementen wie z.B. dem ADS1256 ist bereits eine Offset- und Verstärkungskalibrierung integriert, wodurch sich die Situation wesentlich verbessert. Für dieses Bauelement wird der Offsetfehler nach der Kalibrierung mit einem Wert angegeben, der dem Pegel des Rauschens entspricht. Ein besserer Wert lässt sich nicht erreichen, wodurch der Offsetfehler im direkten Verhältnis zur Auflösung steht. Der Verstärkungsfehler nach der Kalibrierung beträgt ±0,005 % bzw. ca. ±800 Codes, was ebenfalls viel besser dem Wert für die Auflösung entspricht. Bei sehr hoch auflösenden ADCs kann daher eine hohe Genauigkeit nur mit einer Offsetund Verstärkungskalibrierung erreicht werden.
Nach der Beseitigung von Offsetund Verstärkungsfehlern bleibt jetzt noch die INL, die Kurve der Übertragungsfunktion. Während Offset- und Verstärkungsfehler mittels Kalibrierung ohne größere Schwierigkeiten beseitigt werden können, ist die Beseitigung der INL sehr schwierig und kann, wenn überhaupt, nur selten von einem ADC-Anwender durchgeführt werden. Nur wenige verfügen über die Ausrüstung oder die Zeit, die für eine Mehrpunktkalibrierung erforderlich wäre.
Daraus wird deutlich, dass es letztlich die INL ist, die bei den meisten Anwendern die Genauigkeit begrenzt. Bei einem Bauelement wie dem ADS1256 beträgt die INL 0,001 % des Skalenendwertes bzw. ±167 Codes. Dies entspricht gut der Genauigkeit, die man bei dieser Auflösung erwarten kann.
- Datenblätter von A/D-Wandlern richtig interpretieren
- Datenblätter von A/D-Wandlern richtig interpretieren
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Mixed-Signal-ICs
Digitale Features in schnellen D/A-Wandlern
Vorsicht Kleingedrucktes
Datenblätter richtig interpretieren
SAR oder ΔΣ?
Welche Datenwandler-Architektur ist die Richtige?
