Analog Digital Umsetzer
AC- und DC-Signale erfassen – ganz einfach
Um Abtastphänomene wie Aliasing-Effekte und kapazitive Rückwirkungen an den Eingängen zu unterbinden, werden Filter und Verstärker eingesetzt, die selbst unerwünschte Effekte mitbringen. AC- und DC-Signale präzise zu digitalisieren ist eine Herausforderung – und kann doch ganz einfach sein.
An der Digitalisierung von Daten sind mit der Abtastung und der Quantisierung zwei grundlegende Prozesse beteiligt (Bild 1). Der erste Schritt ist die Abtastung, bei der ein zeitlich variables analoges Signal x(t) mit der Abtastfrequenz fS in ein zeitdiskretes Signal x(n) umgewandelt wird. Die Abtastwerte sind in gleichmäßige Zeitabstände von 1/TS unterteilt (fS = 1/TS).
Jobangebote+ passend zum Thema
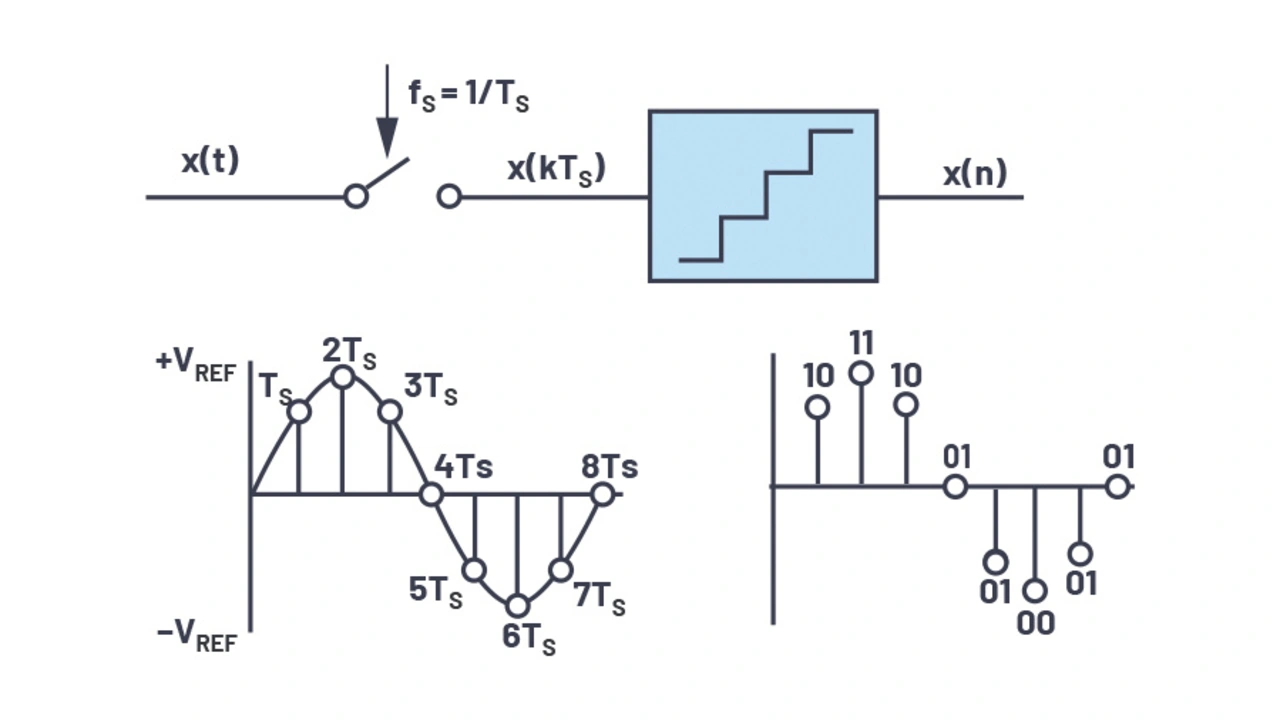
Der zweite Schritt ist die Quantisierung, bei der Wert der zuvor erfassten zeitdiskreten Signalproben an einen der endlich vielen möglichen Werte angenähert und als digitaler Code ausgegeben wird, wie in Bild 1 gezeigt. Da diese Quantisierung wie erwähnt auf endlich viele Werte erfolgt, entsteht bei der Digitalisierung unweigerlich ein Fehler, der als Quantisierungsrauschen bezeichnet wird.
Eine weitere Folge des Abtastprozesses sind Aliasing-Effekte, die durch das Zurückfalten von Eingangssignalen und ihren Oberschwingungen um die Taktfrequenz der Abtast- und Haltestufe entstehen. Das Nyquist-Kriterium besagt, dass die Abtastfrequenz mindestens doppelt so hoch sein muss wie die höchste im Signal enthaltene Frequenz. Wird dieses Kriterium nicht erfüllt, kommt es zu dem als Aliasing bekannten Phänomen.
Um die Folgewirkungen der Aliasing-Effekte im Zeit- und Frequenzbereich verstehen zu können, wird zunächst die Zeitbereichs-Darstellung einer sinusförmigen Spannung betrachtet (Bild 2).
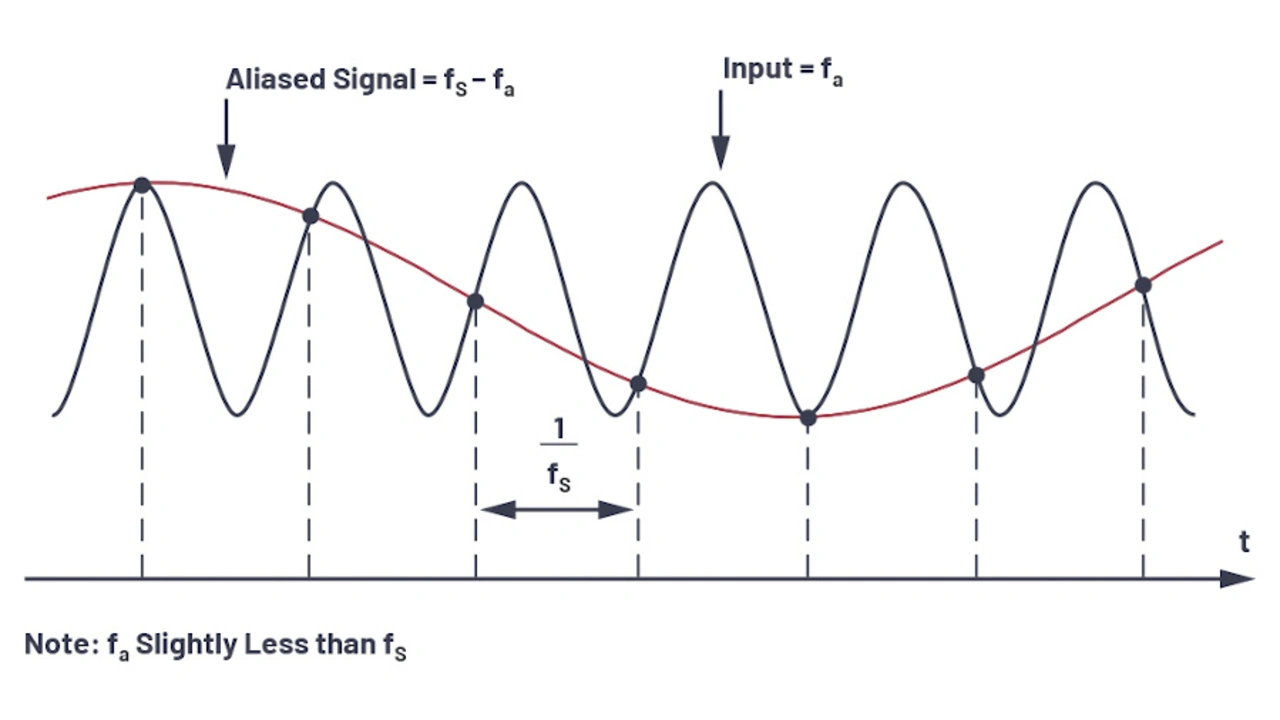
In diesem Beispiel beträgt die Abtastfrequenz fS nicht annähernd das Doppelte der analogen Eingangsfrequenz fa, sondern ist nur geringfügig höher als diese. Das Nyquist-Kriterium ist somit nicht erfüllt. Wie in Bild 2 zu sehen, entsteht durch Aliasing-Effekte eine zusätzliche Sinusschwingung mit der Frequenz fS – fa.
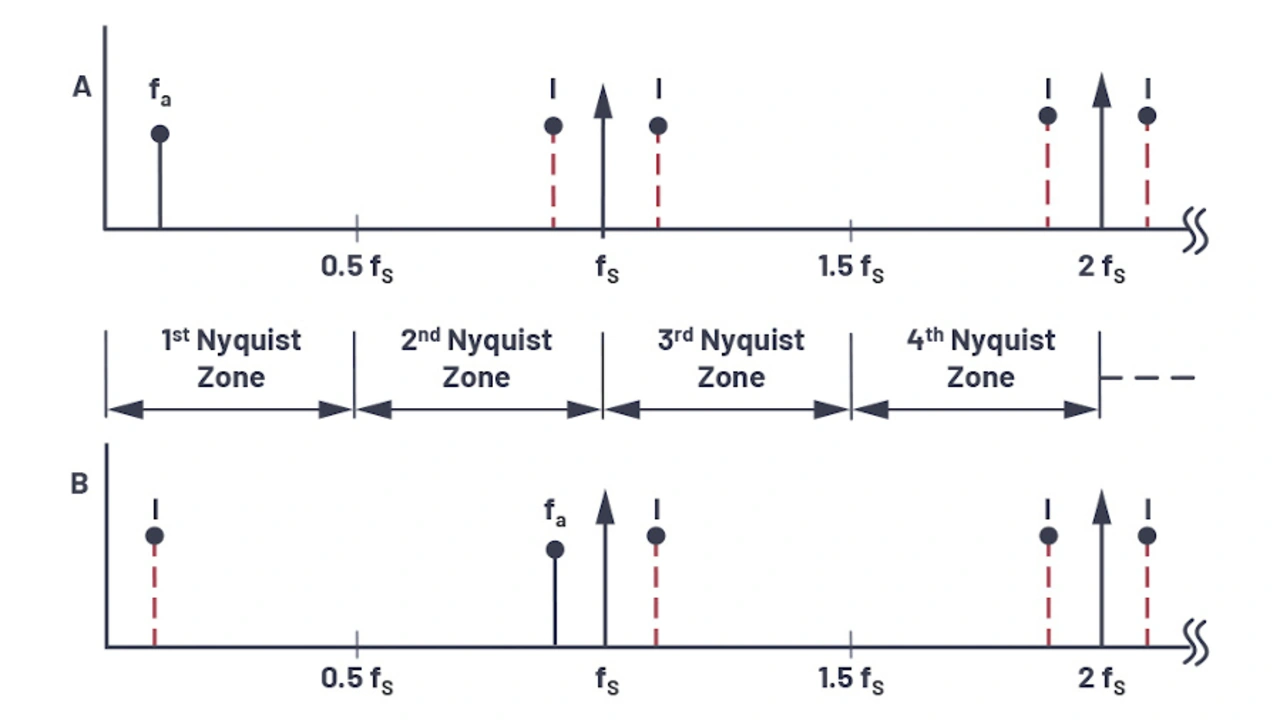
In Bild 3 ist dasselbe Szenario im Frequenzbereich wiedergegeben. Der Frequenzbereich von DC bis fS/2 wird als Nyquist-Bandbreite bzw. erste Nyquist-Zone bezeichnet. Das Frequenzspektrum teilt sich in eine unendliche große Zahl von Nyquist-Zonen auf, die alle eine Breite von fS/2 haben. In der Praxis wird das ideale Abtastglied durch einen ADU mit einem anschließenden FFT-Prozessor (Fast Fourier Transform) ersetzt. Letzterer erzeugt nur einen Ausgang von DC bis fS/2, also jene Signale oder Aliasing-Produkte, die in der ersten Nyquist-Zone auftreten.
Als Beispiel wird der Fall betrachtet, bei dem eine einzelne Sinusschwingung mit der Frequenz fa durch ein ideales Impuls-Abtast-Halte-Glied mit der Frequenz fS abgetastet wird (siehe Bild 1). Die Abtastfrequenz fS soll außerdem größer als 2 × fa sein. Das Ausgangssignal der Abtastschaltung enthält Aliasing-Produkte oder Abbilder des ursprünglichen Signals bei allen Vielfachen von fS, also bei den Frequenzen:
für K = 1, 2, 3, 4 usw.
Im nächsten Fall befindet sich das Eingangssignal außerhalb der ersten Nyquist-Zone (Bild 3). Seine Signalfrequenz ist nur geringfügig kleiner als die Abtastfrequenz – wie in der Zeitbereichs-Darstellung in Bild 2 wiedergeben. Obwohl das Signal außerhalb der ersten Nyquist-Zone liegt, fällt ihr Abbild (ihr Alias) von fS – fa in diese Zone hinein.
Hindernisse auf dem Weg zu präziser Signalerfassung
In anspruchsvollen Anwendungen sind die Entwickler gefordert, die durch Quantisierungsrauschen, Aliasing-Effekte und Eingang mit Schalter-Kondensator-Filter (Switched Capacitor) entstehenden Probleme zu lösen. Die von der Industrie angebotenen zwei Arten von Präzisions-ADUs, also SAR-ADUs (Successive Approximation Register) und Sigma-Delta-ADUs, werden mit Abtastverfahren auf der Basis geschalteter Kondensatoren konzipiert.
Quantisierungsrauschen
In einem idealen Nyquist-ADU entscheidet die Größe des LSB des ADUs über das Quantisierungsrauschen, welches dem Eingangssignal im Zuge der Analog-Digital-Umsetzung hinzugefügt wird. Um diesem Quantisierungsrauschen, das sich auf eine Bandbreite von fS/2 verteilt, entgegenzuwirken, bietet sich als erste Technik die so genannte Überabtastung (Oversampling) an. Hierbei erfolgt die Abtastung des Eingangssignals mit einer Frequenz, die weit über der Nyquist-Frequenz liegt, um auf diese Weise den Signal-Rauschabstand (SNR, Signal to Noise Ratio) und die Auflösung (ENOB, Effective Number Of Bits) zu erhöhen. Beim Oversampling wird die Abtastfrequenz so gewählt, dass sie das N-Fache der Nyquist-Frequenz (2 × fIn) – mit fIn für die interessierende Signalbandbreite – beträgt, sodass sich das Quantisierungsrauschen entsprechend auf das N-Fache der Nyquist-Frequenz verteilt. Hierdurch werden auch die Anforderungen an das Anti-Aliasing-Filter reduziert. Das Oversampling-Verhältnis (Oversampling Ratio, OSR) ist als fS/(2 × fIn) definiert. Allgemein gilt, dass eine Überabtastung des ADUs um den Faktor vier die Auflösung um ein Bit erhöht, was einer Zunahme des Dynamikbereichs um 6 dB entspricht. Ein Vergrößern des Oversampling-Verhältnisses führt zu einer Reduzierung des Gesamtrauschens, und die durch das Überabtasten erzielte Verbesserung des Dynamikbereichs ΔDR beträgt 10 × log OSR (in dB).
Das Oversampling wird stets im Verbund mit einer integrierten Digitalfilter- und Dezimierungsfunktion genutzt und implementiert. Der elementare Oversampling-Modulator in einem Sigma-Delta-ADU formt das Quantisierungsrauschen so, dass es zu einem Großteil aus der interessierenden Signalbandbreite herausgeschoben wird, woraus eine Zunahme des Gesamt-Dynamikbereichs bei niedrigen Frequenzen resultiert (Bild 4).
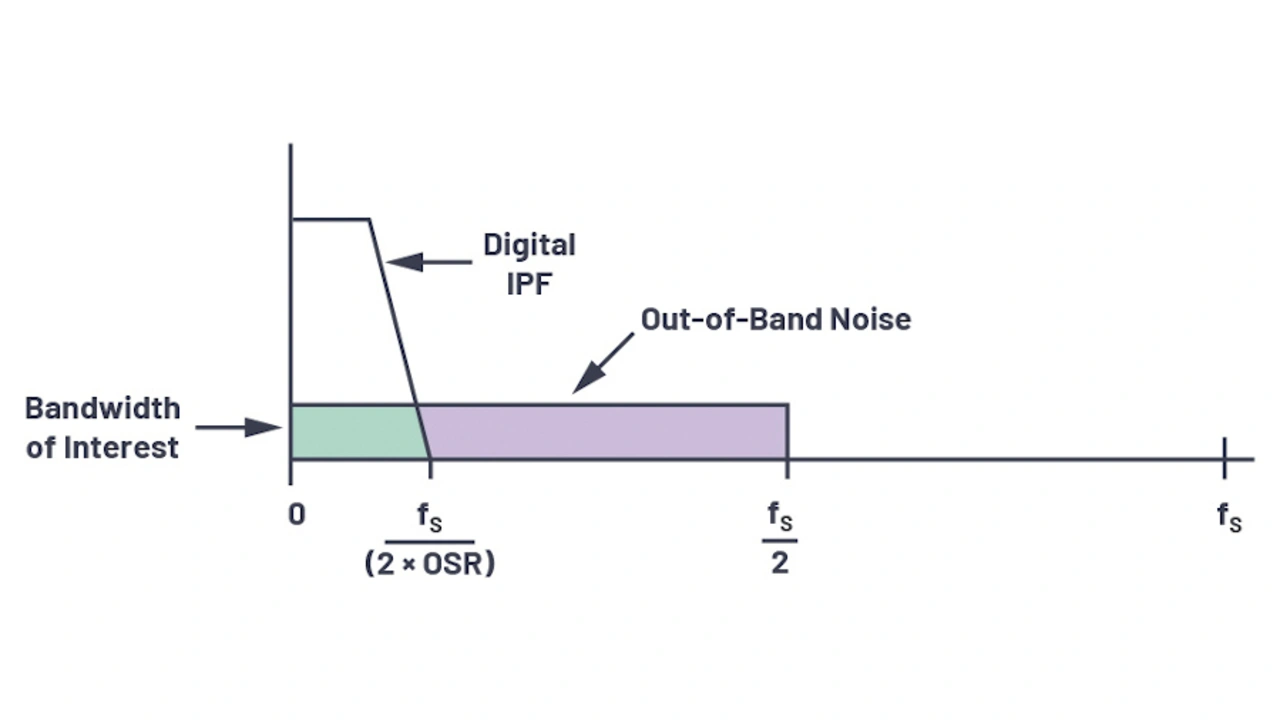
Das digitale Tiefpassfilter (Low-Pass Filter, LPF) entfernt nachfolgend das Quantisierungsrauschen außerhalb der interessierenden Signalbandbreite und der Dezimator reduziert die Ausgangs-Datenrate wieder auf die Nyquist-Rate.
Die Rauschformung (Noise Shaping) ist eine weitere Technik, mit der sich das Quantisierungsrauschen verringern lässt. In Sigma-Delta-ADUs wird ein gering auflösender Quantisierer (1 bis 5 bit) in einer Schleife nach dem Schleifenfilter eingesetzt. Ein DAU dient als Rückkopplung-Glied dazu, das quantisierte Signal vom Eingangssignal zu subtrahieren, wie in Bild 5 gezeigt.
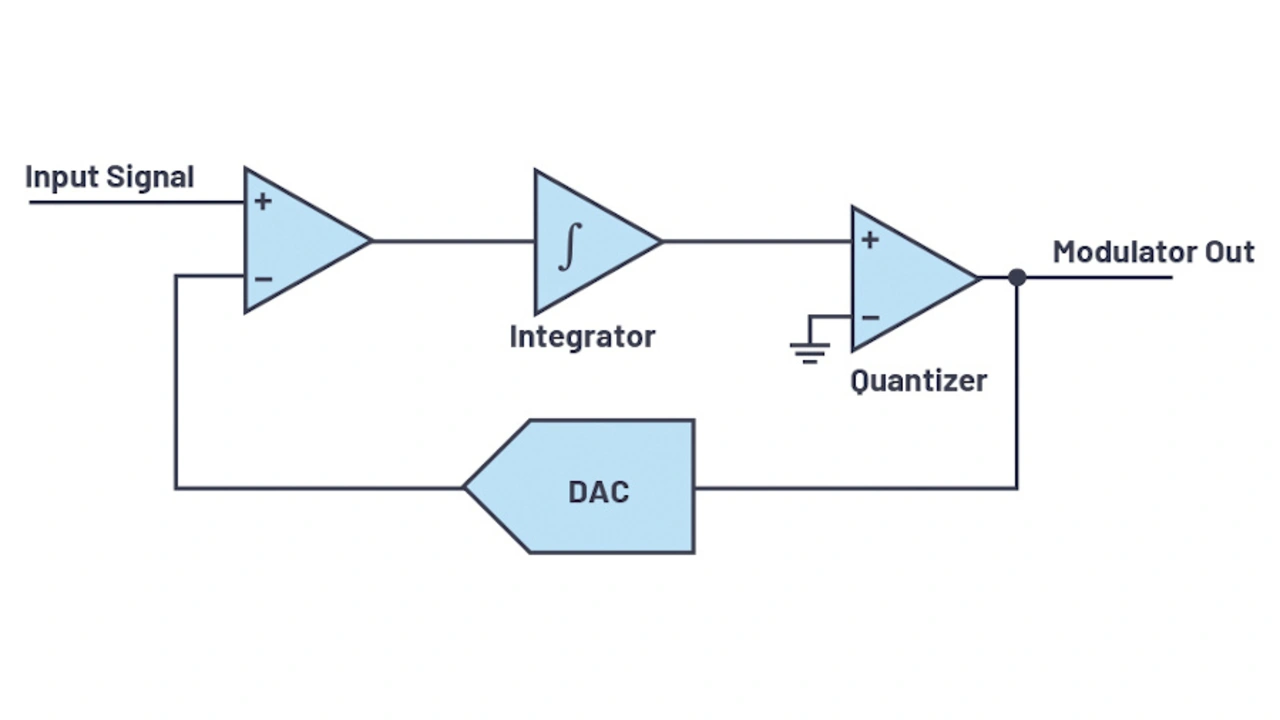
Der Integrator summiert den Quantisierungsfehler fortlaufend auf, was zur Verschiebung des Quantisierungsrauschens hin zu höheren Frequenzen führt, wo es anschließend mit einem digitalen Filter herausgefiltert werden kann. Bild 6 illustriert die spektrale Leistungsdichte (Power Spectral Density, PSD) des Ausgangs x(n) eines typischen Sigma-Delta-ADUs. Die Steilheit des Noise Shapings richtet sich nach der Ordnung des Schleifenfilters H(z) (siehe Bild 11) und beträgt (20 × n) dB/Dekade, wobei n die Ordnung des Schleifenfilters angibt.
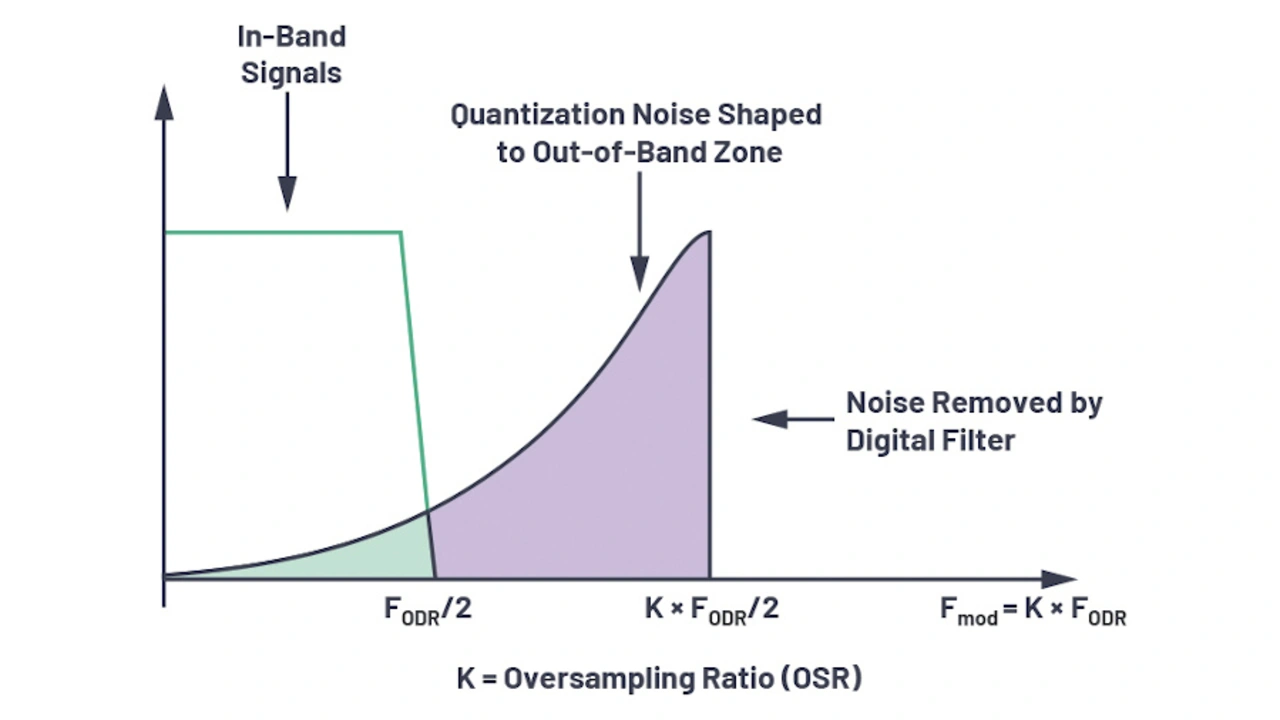
Der Sigma-Delta-ADU erzielt innerhalb des Nutzbandes (In-Band) eine hohe Auflösung, indem er das Noise Shaping mit dem Oversampling kombiniert. Die Nutzbandbreite beträgt fODR/2, wobei ODR für die Ausgangs-Datenrate (Output Data Rate) steht. Um die Auflösung zu erhöhen, kann die Ordnung des Schleifenfilters oder das Oversampling-Verhältnis (OSR) angehoben werden.
Aliasing
Um Aliasing-Effekten in anspruchsvollen Anwendungen entgegenzuwirken, kommen Anti-Aliasing-Filter höherer Ordnung zum Einsatz, damit jegliche Rückfaltungsphänomene sicher vermieden werden. Ein Anti-Aliasing-Filter ist ein Tiefpassfilter, das die Bandbreite des Eingangssignals begrenzt und sicherstellt, dass es jenseits der interessierenden Bandbreite keine Frequenzkomponenten gibt, die zurückgefaltet werden können. Die nötige Leistungsfähigkeit des Filters hängt davon ab, wie nah das obere Bandende an fS/2 liegt und welche Dämpfung erforderlich ist.
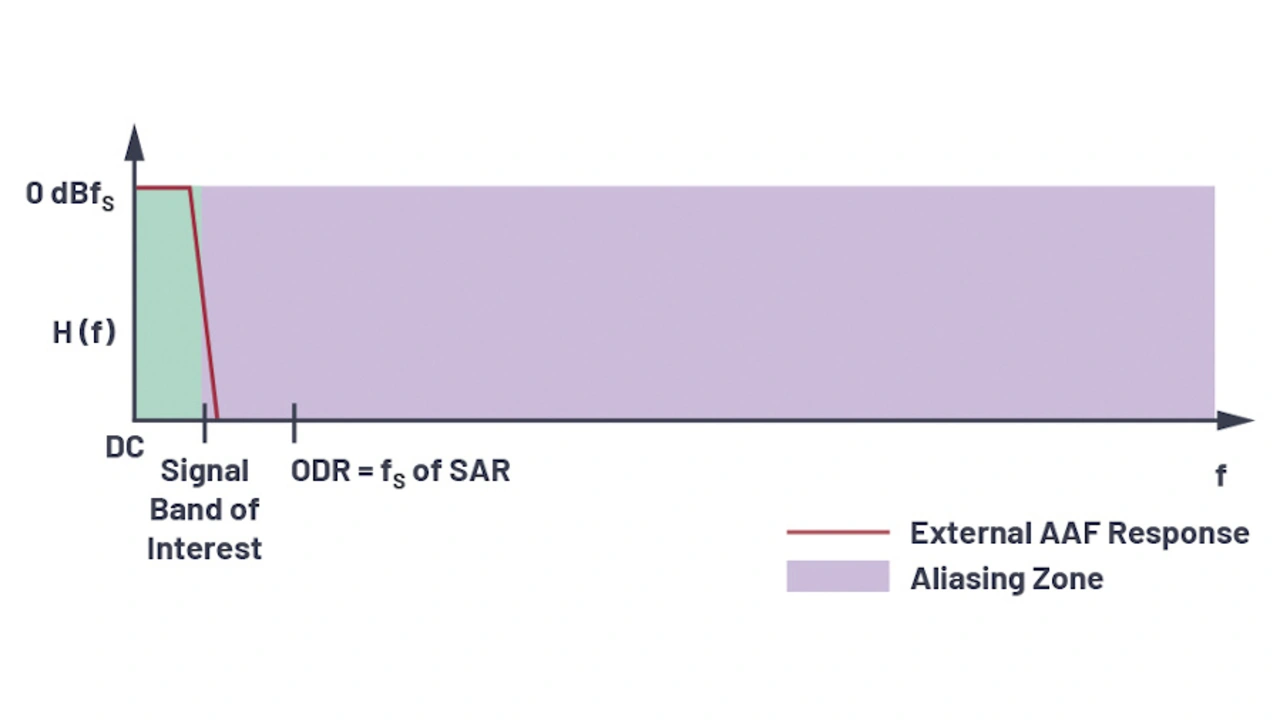
Bei SAR-ADUs ist der Abstand zwischen der Bandbreite des Eingangssignals und der Abtastfrequenz oft nicht sehr groß. Hier benötigen Entwickler deshalb ein komplexes Filter höherer Ordnung, das mehr Strom braucht und höhere Verzerrungen verursacht. Wenn beispielsweise ein SAR-ADU mit einer Abtastrate von 200 kHz eine Eingangsbandbreite von 100 kHz hat, muss das Anti-Aliasing-Filter Eingangssignale oberhalb 100 kHz stark unterdrücken, um sicherzustellen, dass keine Aliasing-Effekte auftreten. Dies aber verlangt nach einem Filter sehr hoher Ordnung. Bild 7 zeigt den erforderlichen, sehr steilen Kennlinienverlauf.
Wird eine Abtastrate von 400 kHz gewählt, um die Anforderungen an die Ordnung des Filters zu reduzieren, ist die Unterdrückung von Eingangsfrequenzen erst oberhalb 300 kHz gefordert. Das Anheben der Abtastrate erhöht jedoch den Stromaufnahme, denn tatsächlich verdoppelt sich bei einer doppelt so hohen Abtastrate auch die Leistungsaufnahme. Zusätzliches Oversampling mit Inkaufnahme einer höheren Stromaufnahme reduziert die Anforderungen an das Anti-Aliasing-Filter weiter, da die Abtastfrequenz nennenswert größer wird als die Eingangsbandbreite.
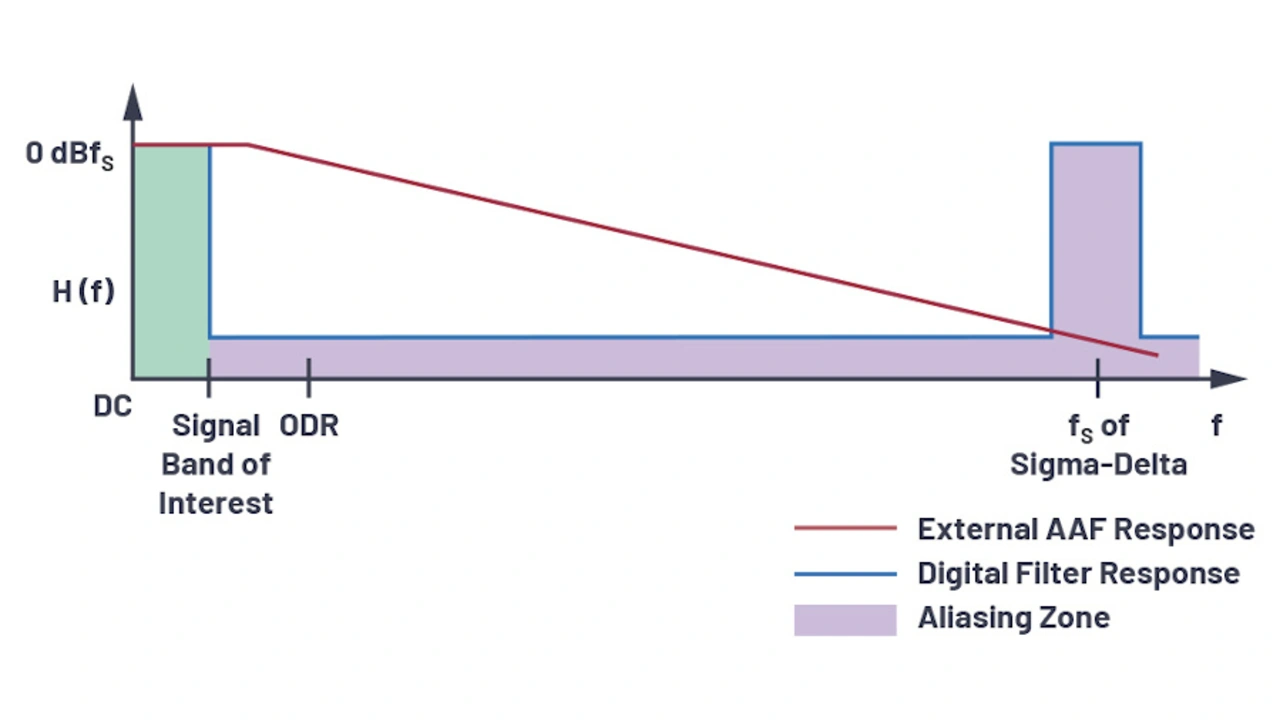
Bei Sigma-Delta-ADUs wird das Eingangssignal in einem wesentlich höheren Verhältnis überabgetastet. Die Abtastfrequenz ist deshalb deutlich größer als die Eingangsbandbreite, und entsprechend geringer sind die Anforderungen an das Anti-Aliasing-Filter (siehe Bild 8).
Bild 9 vermittelt einen Eindruck von der Komplexität des Anti-Aliasing-Filters für SAR-ADUs und zeitdiskrete Sigma-Delta-Schaltungen (Discrete-Time Sigma-Delta, DTSD).
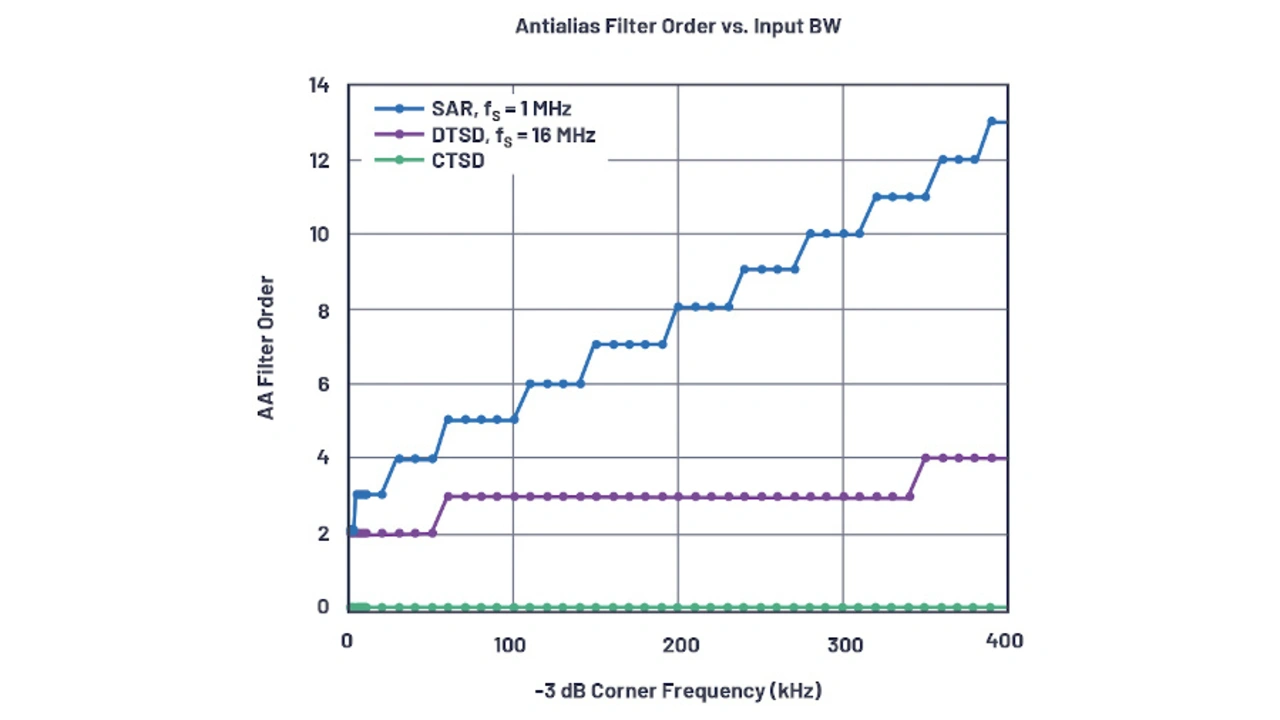
Wird eine 3-dB-Eingangsbandbreite von 100 kHz gewählt, um bei der Abtastfrequenz fS eine Dämpfung von 102 dB zu erzielen, reicht für einen DTSD-ADU ein Anti-Aliasing-Filter zweiter Ordnung aus. Dagegen wird bei einem SAR-ADU ein Filter fünfter Ordnung benötigt, um bei fS dieselbe Dämpfung zu erreichen.
Bei einem zeitkontinuierlichen Sigma-Delta-ADU (Continuous-Time Sigma-Delta, CTSD) erfolgt die Dämpfung inhärent, sodass keinerlei Anti-Aliasing-Filter erforderlich ist.
Diese Filter können für Entwickler ein neuralgischer Punkt sein, denn sie müssen auf Ebenheit im interessierenden Frequenzband optimiert werden und gleichzeitig eine möglichst große Dämpfung bieten. Sie verursachen ferner eine Vielzahl weiterer Fehler – z.B. Offset-, Verstärkungs- und Phasenfehler sowie Rauschen – in der Gesamtschaltung und beeinträchtigen damit deren Leistungsfähigkeit.
Hinzu kommt, dass Hochleistungs-ADUs prinzipbedingt differenziell sind, sodass die doppelte Anzahl passiver Bauelemente benötigt wird. Um in mehrkanaligen Anwendungen eine bessere Phasenanpassung zu erreichen, müssen sämtliche Bauelemente im Signalpfad gut aufeinander abgestimmt sein, weshalb enger tolerierte Bauelemente benötigt werden.
Eingang mit geschaltetem Kondensator
Die Qualität der Abtastung eines Eingangssignals mit der Schalter-Kondensator-Technik hängt von der Einschwingzeit des abgetasteten Signals an einem Kondensator ab und geht mit einem vorübergehenden Lade- bzw. Entladestrom beim Ein- bzw. Ausschalten des Abtastschalters einher. Dies wird als Kickback (Rückschlag) auf den Eingang bezeichnet und verlangt nach einem eingangsseitigen Verstärker, der für diese kurzzeitigen Spitzenströme ausgelegt ist. Außerdem ist es notwendig, dass sich der Eingang am Ende des Abtastintervalls stabilisiert hat. Die Genauigkeit des abgetasteten Eingangssignals entscheidet über die Leistungsfähigkeit des ADUs. Dies impliziert, dass sich der Eingangsverstärker nach dem Kickback-Ereignis schnell stabilisieren muss. Benötigt wird somit ein breitbandiger Verstärker, der kurze Einschwingzeiten unterstützt und die Rückwirkung der Schalter-Kondensator-Operation absorbieren kann.
Wenn der Abtastschalter von Schalter-Kondensator-Eingängen eingeschaltet ist, muss der Eingangsverstärker umgehend den Ladestrom für den Halte-Kondensator liefern. Diese plötzliche Stromspitze kann nur dann zeitgerecht ermöglicht werden, wenn der Verstärker über eine hinreichende Bandbreite verfügt. Wegen der parasitären Effekte des Schalters kommt es zum Zeitpunkt der Abtastung zu einer Rückwirkung auf den Eingangsverstärker. Stabilisiert sich der Verstärkerausgang nicht bis zur nächsten Abtastung, wird das Eingangssignal fehlerhaft erfasst, sodass der ADU-Eingang entsprechend verfälscht wird.
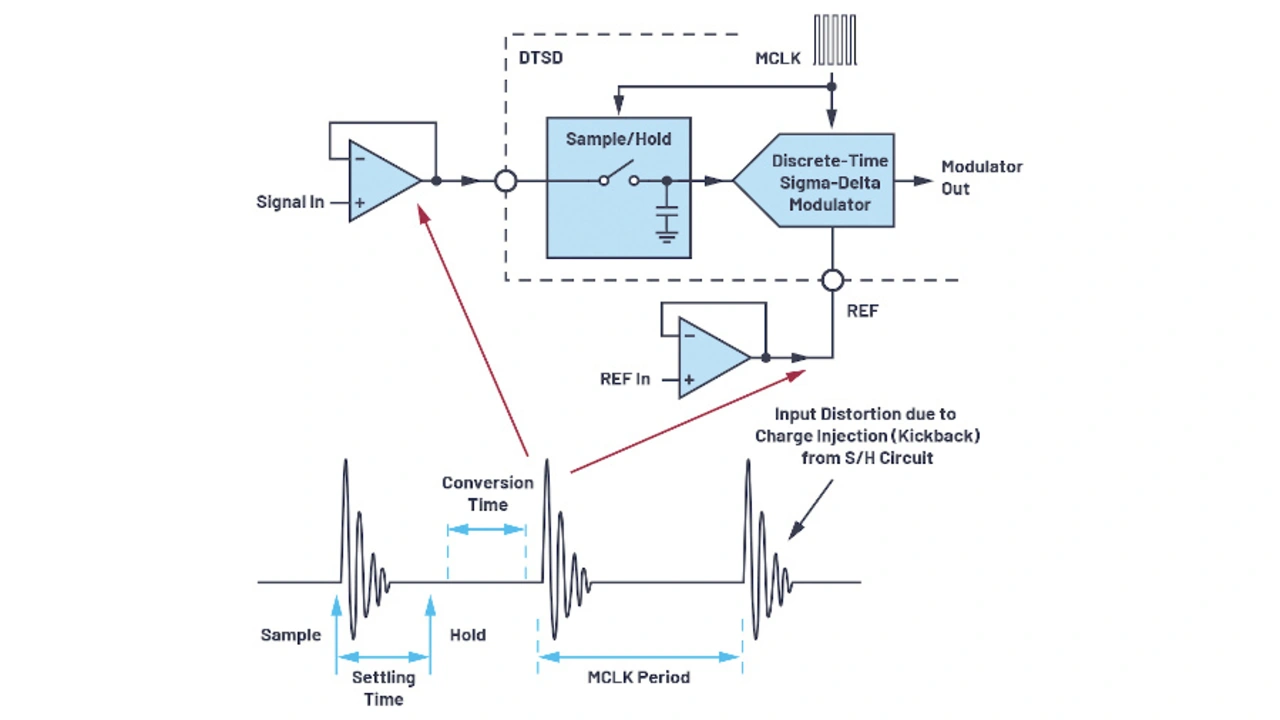
In Bild 10 ist das Kickback-Phänomen an einem DTSD-ADU dargestellt. Beträgt die Abtastfrequenz beispielsweise 24 MHz, muss sich das Datensignal binnen 41 ns stabilisieren. Da die Referenz ebenfalls ein Schalter-Kondensator-Eingang ist, wird auch am Referenzeingang ein breitbandiger Verstärker (Puffer) benötigt. Diese Verstärker für das Eingangssignal und das Referenzsignal erhöhen das Rauschen und beeinträchtigen die allgemeine Leistungsfähigkeit der gesamten Signalverarbeitung. Abgesehen davon führen die Verzerrungskomponenten aus dem eingangsseitigen Verstärker in der Umgebung der Abtast- und Haltefrequenz dazu, dass sich die Anti-Aliasing-Anforderungen erhöhen. Hinzu kommt schließlich auch, dass bei Schalter-Kondensator-Eingängen etwaige Änderungen der Abtastrate zu einem variierenden Eingangsstrom führen. Dies kann ein erneutes Abstimmen des Systems erforderlich machen, um den im Eingangsverstärker oder in der vorangehenden Stufe beim Ansteuern des ADUs entstehenden Verstärkungsfehler zu verringern.
- AC- und DC-Signale erfassen – ganz einfach
- Zeitkontinuierliche Sigma-Delta-ADUs