Labormesstechnik
Mathematik als nützliches Messtechnik-Tool
Fortsetzung des Artikels von Teil 1
Anwendungen mit dem Mathematikbaustein
Messung transienter Leistung
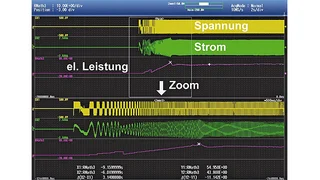
Mit der implementierten Leistungsfunktion lässt sich z.B. die transiente Wirkleistung für jede Periode messen. Dabei werden die Momentanwerte der Leistung (Momentanwerte aus „Strom mal Spannung“) über eine Periodendauer integriert. Für jede Periode wird die Berechnung wiederholt und das Ergebnis aktualisiert/aufsummiert. Auf diese Weise lassen sich auch Änderungen der elektrischen Leistung präzise registrieren, selbst wenn die Periodendauer der Wechselspannung schwankt. Wenn sich z.B. die Periodendauer während des Hochlaufs eines Motors kurzfristig ändert, kann das Gerät mit dieser Funktion den Änderungen der Periodendauer folgen und die elektrische Leistung in Echtzeit für jeden Zyklus der Kurve registrieren. Mit einer Rechenkapazität von 10 MS/s erfasst der Recoder alle Daten und berechnet z.B. die elektrische Leistung von Pulsbreitenmodulations-Kurven (PWM) bei Geräten wie Umrichtern. Bild 2 zeigt als Beispiel die elektrische Leistungsmessung beim Hochlauf eines Motors.
Jobangebote+ passend zum Thema
Messtechnik-Tools für Oszilloskope der Bilder 2 bis 8
Phasendifferenz mechanischer/elektrischer Winkel
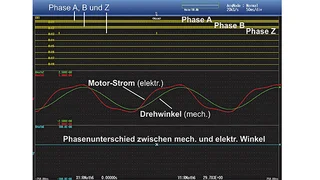
Zur Energieeinsparung bei Motoren werden häufig Umrichter und Vektorsteuerungen verwendet. Die Drehmomentcharakteristiken von Motoren hängen dabei von der Phasendifferenz zwischen dem mechanischen Positionswinkel eines Motors (Absolutwinkel der Motorwelle) und dem zugehörigen elektrischen Phasenwinkel eines Erregerstroms ab. Aus diesem Grund ist die Messung eines elektrischen Phasenwinkels und des dazugehörigen mechanischen Positionswinkels (bzw. deren Phasendifferenz) wichtig, um Motorcharakteristiken zu verstehen.
Für diesen Zweck gibt es in der Mathematik-Bibliothek eine Phasendifferenz-Berechnung, die sich aus dem mechanischem Positionswinkel (z.B. Drehgeber-Signal von der Motorwelle) und dem elektrischen Phasenwinkel ergibt. Dabei kommt eine diskrete Fouriertransformation des Erregerstroms zur Anwendung. Der elektrische Phasenwinkel kann so für jeden Zeitpunkt berechnet und registriert werden, auch wenn die Kurven des Stroms verzerrt sind. Bild 3 zeigt ein Beispiel für die Messung des elektrischen Phasenwinkels bei verzerrten Kurven des Stroms.
Rundlauf-Geometrie visualisieren
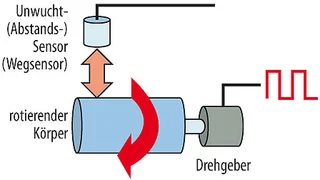
Die Echtzeit-Mathematikfunktion ermöglicht es beispielsweise auch, die Ergebnisse einer Rundlauf- bzw. Unwucht-Messung eines rotierenden Körpers in XY-Koordinaten (berechnet aus Polarkoordinaten) zu visualisieren. Bild 4 zeigt das Prinzip, Bild 5 ein zugehöriges Oszillogramm. Das Verhalten des rotierenden Körpers kann in Polarkoordinaten in Echtzeit angegeben werden, indem die Winkelfunktion zur Berechnung des Winkels auf Basis des Drehgeber-Signals verwendet wird, die Sinus- und Cosinuswerte aufgrund dieses Wertes berechnet werden und die XY-Anzeigefunktion zur Anzeige jedes Wertes auf den Koordinaten herangezogen wird. In die Anzeige einbezogen wird das Signal des Abstands-/Unwucht-Sensors, der in der Praxis meist ein Wegsensor ist. Durch die unten in Bild 5 gezeigte XY-Koordinaten-Darstellung kann man das Verhalten des sich drehenden Körpers in Abhängigkeit vom Drehwinkel darstellen.
Messung mit einem Resolver-Winkelsensor
In der Vergangenheit wurden Resolver häufig zur Erfassung der geometrischen Motor-Drehwinkel von Fahrzeugen aller Art verwendet, da sie hervorragend auch unter schlechten Umgebungsbedingungen einsetzbar sind. Wie Bild 6 zeigt, wird in den Rotor eines Resolvers eine Erregerspannung eingespeist. Bei Drehung des Rotors (und damit des Untersuchungsobjekts „Motor“) liefert der Resolver dann aus zwei festen, orthogonal zueinander angeordneten Stator-Sensorspulen zwei Signale (sin Θ und cos Θ), die dem mechanischen Drehwinkel Θ direkt zugeordnet werden können. Die Erregerspannung ist den Signalen von sin Θ und cos Θ überlagert, so dass diese Trägerkomponente zu entfernen ist und dann die Winkelberechnung ausgeführt werden kann.
Die Resolver-Funktion im ScopeCorder erkennt dabei automatisch die Signale von sin Θ und cos Θ, die synchron zur Erregerspannung des Resolvers sind, tastet sie ab und berechnet die Winkel. Die Resolver-Funktion besitzt eine interne Nachlauffilter-Schleife, wie Bild 7 darstellt. Auch wenn einige Abtastwerte der Signale von sin Θ und cos Θ fehlen sollten, können sie doch interpoliert werden.
Bild 8 zeigt schließlich das Beispiel einer Messung des Resolver unter Verwendung dieser Funktion. Wie zu erkennen ist, werden die errechneten Winkeldaten nicht von der Erkennung der Synchronisation beeinflusst, und hochgenaue Ergebnisse stehen ohne Unterbrechung zur Verfügung.
Die hier beispielhaft gezeigten Echtzeit-Mathematikfunktion können letztlich die Entwicklung energiesparender Geräte ebenso wie die Effizienz von Analysen und Fehlerdiagnosen im Bereich der Mechatronik und Leistungselektronik, auch bei Automobilen, deutlich im Sinne von Zeitersparnis und Fehlersicherheit unterstützen.
Die Autoren
| Anna Krone |
|---|
| ist bei Yokogawa in Herrsching im Produkt-Support für den ScopeCorder tätig. Sie befasst sich seit langem mit dieser Produktkategorie und arbeitet an praxisgerechten Lösungen für Messaufgaben unterschiedlicher Art. |
| Chiaki Yamamoto |
|---|
| absolvierte sein Ingenieurstudium an der Universität von Yamanashi nahe Tokio. Nach seinem Abschluss 1991 begann er seine Berufslaufbahn am Hauptsitz der Firma Yokogawa. Dort ist er bis heute in verschiedenen Tätigkeitsfeldern im Bereich der mechanischen und elektronischen Produktentwicklung und des Marketing tätig, derzeitig in der Product Marketing Group der Yokogawa Meters & Instruments Corporation. |
- Mathematik als nützliches Messtechnik-Tool
- Anwendungen mit dem Mathematikbaustein