Near Field Communication
Impedanzanpassung für NFC-Anwendungen – Teil 1
Um ein Gerät für die Kommunikation über NFC zu befähigen, braucht ein Entwickler einen Mikrocontroller, einen NFC-Transceiver und eine Antenne. Die Herausforderungen sind dabei das Filter und das Anpassungsnetzwerk, an dem die NFC-Antenne angeschlossen wird.
NFC ist eine Funkkommunikationstechnik mit kurzer Reichweite, hoher Frequenz und niedriger Bandbreite, die eine standardisierte Kommunikation zwischen zwei mobilen Geräten wie Smartphones, Smartcards, Aufklebern oder Tags ermöglicht. Weil sie in Smartphones integriert ist, erfreut sich NFC großer Beliebtheit. Im Gegensatz zu den vergleichbaren RFID-Standards auf der gleichen Frequenz von 13,56 MHz eignet sich NFC dank der kurzen Reichweite von unter 10 cm besser für sensible Anwendungen wie Finanztransaktionen.
Die Auslegung der Filter- und Anpassungsschaltung zur Kopplung des NFC-Transceivers mit der Antenne ist komplex in der Berechnung, und aufgrund von Toleranzen der Bauelemente können zusätzlich Iterationen nötig werden. Die Auslegung dieser Schaltung ist im Folgenden das Thema.
Jobangebote+ passend zum Thema
Theorie der konjugiert komplexen Impedanzanpassung
Die konjugiert komplexe Impedanzanpassung ist ein sehr wichtiges Verfahren im HF-Schaltungsentwurf, um die maximal mögliche Leistungsübertragung zwischen einer Quelle und ihrer Last zu gewährleisten und die Signalreflexionen von der Last zu minimieren. Ein Beispiel für die Notwendigkeit der Leistungsübertragung findet sich in der Eingangsstufe eines jeden empfindlichen HF-Empfängers. Es liegt auf der Hand, dass unnötige Verluste in einer Schaltung, die bereits extrem kleine Signalpegel führt, einfach nicht toleriert werden können. Daher wird in den meisten Fällen schon beim anfänglichen Entwurf äußerst sorgfältig darauf geachtet, dass jede Stufe auf ihre Last abgestimmt ist.
In der Hochfrequenztechnik sind Lasten oft komplex, d.h. sie haben zusätzlich zu ihrem ohmschen Anteil eine induktive oder kapazitive Komponente. Zur Anpassung muss der induktive oder kapazitive Anteil mit seinem Gegenstück, dem sogenannten konjugiert komplexen Anteil, kompensiert werden. Das bedeutet, dass z.B. eine induktive Komponente kapazitiv kompensiert werden muss.
![Schaltbild einer Signalquelle mit Innenimpedanz ZQ und der Lastimpedanz ZL [2]. Schaltbild einer Signalquelle mit Innenimpedanz ZQ und der Lastimpedanz ZL [2].](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1638955151-270-worryqg1t.jpg.1280x0.webp)
Die Impedanzanpassung basiert auf dem Theorem der maximalen Leistungsübertragung. Es besagt, dass, um die maximale externe Leistung aus einer Quelle mit einem endlichen Innenwiderstand zu erhalten, der Widerstand der Last gleich dem Widerstand der Quelle, von ihren Ausgangsanschlüssen aus gesehen, sein muss. Zusätzlich besagt es, dass jede reaktive Komponente der Quelle und der Last gleich groß, aber mit entgegengesetztem Vorzeichen sein sollte. Dies bedeutet, dass die Impedanzen von Last und Quelle konjugiert komplex zueinander sein müssen [1].
Im Allgemeinen hat die Impedanz
das konjugiert Komplexe
wobei R der Realteil und X der Imaginärteil der komplexen Impedanz Z ist. Bild 1 zeigt die komplexe Quellimpedanz ZS und die komplexe Lastimpedanz ZL. Diese Impedanzen müssen die folgende Bedingung erfüllen, um zu einer optimalen Anpassung zu führen:
Es gibt viele mögliche Schaltungen, die für eine Impedanzanpassung verwendet werden können. Die einfachste ist die L-Schaltung, die aus zwei Reaktanzen besteht. Der Name dieser Schaltung ist von der Anordnung der beiden Komponenten abgeleitet, die der Form eines »L« ähnelt [2]. Bild 2 zeigt die beiden möglichen Versionen der L-Schaltung für die Impedanzanpassung.
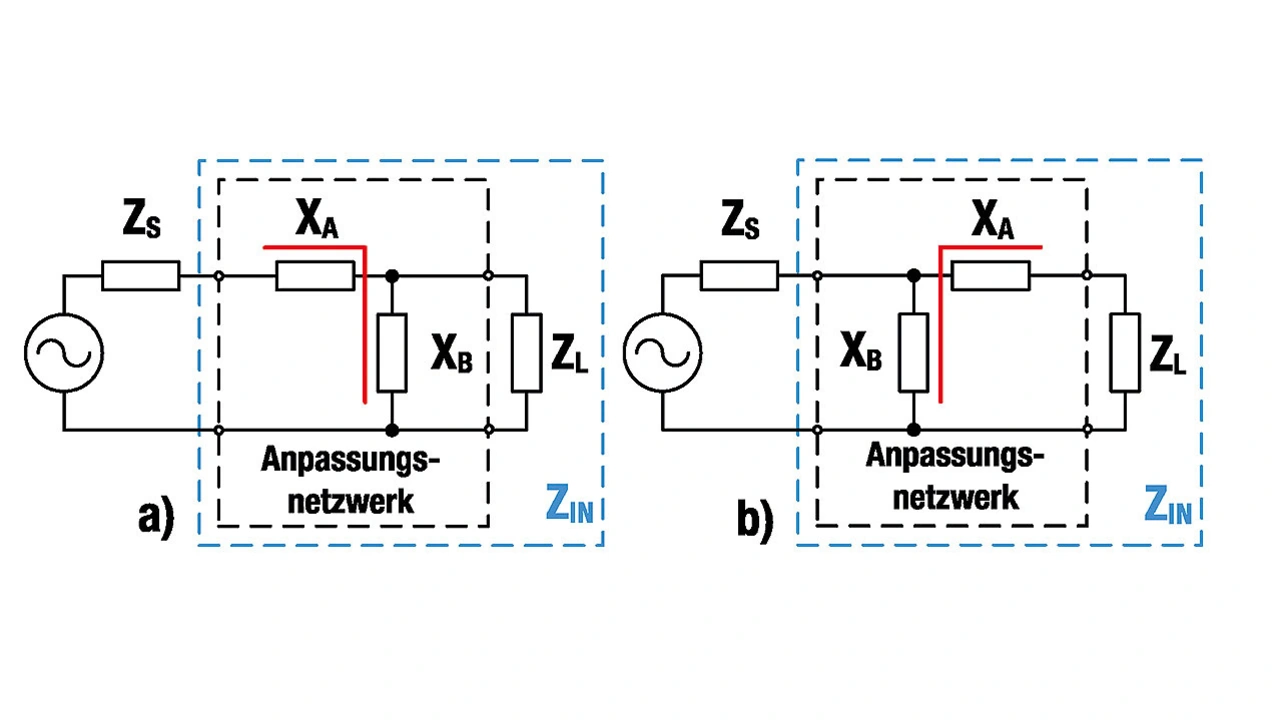
In Bild 2 ist XA die ideale Reaktanz des Serienzweigs und XB die ideale Reaktanz des Parallelzweigs. ZS und ZL sind die Quell- und Lastimpedanzen. Zin bezeichnet die Eingangsimpedanz und beinhaltet die Last- und Anpassungsimpedanz, die das konjugiert Komplexe von ZS sein muss. Bevor die Anpassungskomponenten bestimmt werden können, müssen die Last- und die Quellimpedanz bekannt sein. Die Quellimpedanz beträgt in den meisten Fällen 50 Ω. Im Allgemeinen kann die Quellimpedanz auch komplex sein.
Bestimmung der komplexen Lastimpedanz
Die komplexe Lastimpedanz kann durch Messung und Berechnung bestimmt werden. Die komplexe Impedanzmessung für den 13,56-MHz-Bereich kann mit einem vektoriellen Netzwerkanalysator (VNA) durchgeführt werden, der die S-Parameter des Prüflings bestimmt.
S-Parameter beschreiben das elektrische Verhalten von linearen elektrischen Netzwerken. Für die Impedanzanpassung wird der Parameter S11 verwendet, der als Eingangsreflexionsfaktor bezeichnet wird. Der Eingangsreflexionsfaktor ist eine komplexe Größe, deren Absolutwert ein Indikator für die Reflexion ist. |S11| = 0 bedeutet, dass die Schaltung perfekt angepasst ist und dass keine der einfallenden »Leistungswellen« reflektiert wird. |S11| = 1 bedeutet, dass 100 % der einfallenden Leistungswelle am Eingang reflektiert wird, zurück zur Quelle.
Bei NFC-Anwendungen ist die Last eine Antenne. Für praktische Berechnungen und Simulationen werden die elektrischen Eigenschaften der Antenne in einem Ersatzschaltbild dargestellt. Das vereinfachte Reihenersatzschaltbild einer NFC-Antenne ist in Bild 3 dargestellt.
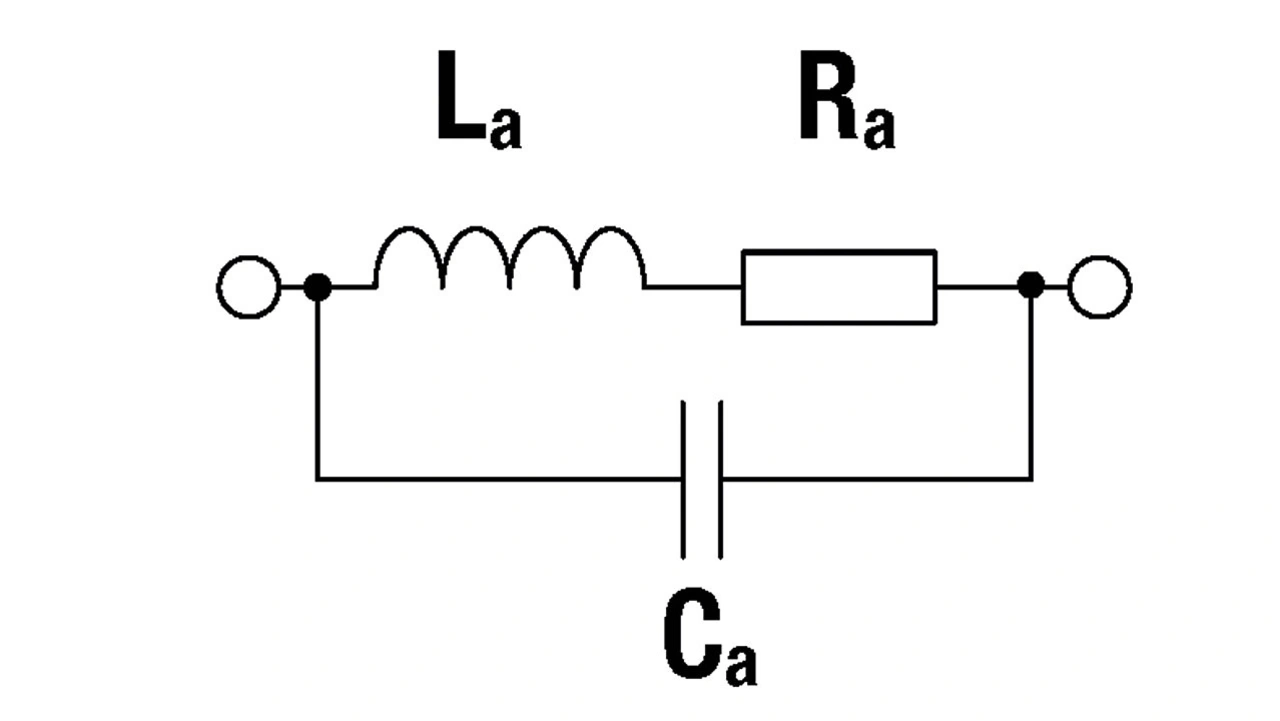
La ist die Induktivität und Ra ist der äquivalente Serienwiderstand, der alle ohmschen Verluste der Antenne repräsentiert. Ca ist die parallele äquivalente Kapazität der Antenne. Die Werte La und Ra können direkt mit einem Netzwerkanalysator oder LCR-Meter gemessen werden.
Der Wert Ca ist ein parasitärer Wert und muss durch Messung und Berechnung bestimmt werden. Die Frequenzabhängigkeiten von La, Ca und Ra werden in den Berechnungen und Simulationen nicht berücksichtigt. Bei Kenntnis der Induktivität La kann die parallele Ersatzkapazität Ca bei der Eigenresonanzfrequenz fS mit Gleichung 4 berechnet werden [3].
Die Eigenresonanzfrequenz fS liegt beim ersten Messpunkt, an dem die komplexe Lastimpedanz real wird. Die Impedanz der Antenne (= ZL), die für die Impedanzanpassung notwendig ist, kann wie folgt berechnet werden:
Der Gütefaktor QL der Antenne ist durch das Verhältnis des Imaginärteils XL und des Realteils RL der Antennenimpedanz definiert und kann daher mit Gleichung 6 berechnet werden.
Bestimmung der Komponenten der Anpassungsschaltung
Das Anpassungsverfahren kann durch Berechnung und Simulation durchgeführt werden. Im Allgemeinen können beide in Bild 2 gezeigten Anpassungsnetzwerke verwendet werden, aber das in Bild 2a gezeigte Netzwerk ist einfacher zu berechnen und wurde deshalb ausgewählt, um das Anpassungsverfahren zu demonstrieren.
Da die Last ein induktives Verhalten hat, sind die Reaktanzen XA und XB kapazitiv. Im Allgemeinen können XA und XB auch induktiv sein, wenn die Last ein kapazitives Verhalten aufweist. XA und XB gelten als ideal, d.h. es wird davon ausgegangen, dass sie keinen ohmschen Anteil haben.
Berechnung der Komponenten der Anpassungsschaltung
Für das in Bild 2a gezeigte Netzwerk wird die perfekte Anpassung für Zin = ZS* erreicht. Zin kann wie folgt berechnet werden [4]:
Unter Berücksichtigung von Gleichung 7 errechnet sich der Real- und Imaginärteil der Eingangsimpedanz Zin:
Wenn die Gleichung 8 für die Reaktanz XB gelöst wird, erhält man zwei verschiedene Werte XB1 und XB2, weil Gleichung 8 eine quadratische Gleichung ist:
Die Reaktanz XA hat ebenfalls zwei Werte, XA1 und XA2, und ergibt aufgrund von Gleichung 9 unter Berücksichtigung von Gleichung 10 den folgenden Ausdruck:
Im zweiten Teil des Aufsatzes wird gezeigt, wie eine Impedanzanpassung für eine NFC-Ausgangsschaltung realisiert werden kann.
Literatur
[1] Cartwright, K.: Non-Calculus Derivation of the Maximum Power
Transfer Theorem, Technology Interface International Journal,
2008, H. 2, pdf" title="http://tiij.org/issues/issues/spring2008/30_Cartwright/ Cartwright-max%20power%20transfer.pdf">http://tiij.org/issues/issues/spring2008/30_Cartwright/
Cartwright-max%20power%20transfer.pdf.
[2] Bowick, C.: RF Circuit Design, 2. Auflage, Newnes, 2007,
ISBN-10: 0750685182.
[3] PN7120 Antenna Design and Matching Guide. NXP, Application
Note, AN11564, 18. April 2016, www.nxp.com/docs/en/applicationnote/
AN11564.pdf.
[4] Baier, T.: Automated Impedance Adjustment of 13.56 MHz NFC
Reader Antennas. Masterarbeit, TU Graz, August 2014, https://diglib.
tugraz.at/download.php?id=582ed236da273&location.
Der Autor

Christian Merz
geboren 1986, studierte Elektrotechnik an der Technischen Hochschule Deggendorf und schloss 2013 mit dem akademischen Grad Master of Science ab. Nach dem Studium arbeitete er als Wissenschaftlicher Mitarbeiter an der Technischen Hochschule Deggendorf zum Thema Energy Harvesting.
Seit Oktober 2018 ist er als Product Manager im Bereich Wireless Power Transfer (WPT) bei Würth Elektronik eiSos tätig. Bis heute veröffentlichte er insgesamt 17 Publikationen zu den Themen Energy Harvesting, Analyse nichtlinearer Schaltungen, Hochgüte-Impedanzanpassung und WPT/NFC.
Christian.Merz@we-online.de