Near Field Communication
Impedanzanpassung für NFC-Anwendungen – Teil 2
Die Herausforderungen für ein NFC-Interface sind das Filter und das Anpassungsnetzwerk, an dem die NFC-Antenne angeschlossen wird. Im ersten Teil [5] wurde in die Theorie der konjugiert komplexen Impedanzanpassung eingeführt. Nun folgt die Impedanzanpassung für eine NFC-Ausgangsschaltung.
Ein NFC-IC hat normalerweise einen differenziellen Ausgang und eine Impedanz von 50 Ω zwischen den Ausgangsanschlüssen TX1 und TX2 (Bild 4). Diese Anschlüsse sind mit einer Schaltung verbunden, die aus einem Filternetzwerk, einer Anpassungsschaltung, Dämpfungswiderständen und einer NFC-Antenne besteht. Der Ausgang des NFC-ICs ist differenziell, um gegen elektromagnetische Störsignale resistent zu sein. Eine typische differenzielle NFC-Ausgangsschaltung ist in Bild 4 dargestellt.
Um das Verständnis der NFC-Ausgangsschaltungskomponenten zu vereinfachen, kann die Differenzialschaltung in eine nicht-symmetrische Schaltung umgewandelt werden.
Jobangebote+ passend zum Thema
Impedanzanpassung für NFC-Anwendungen Bilder 4-6
![. Der Ausgang eines NFC-Transceiver-ICs ist typischerweise differenziell ausgeführt und erfordert eine symmetrische Beschaltung [4] . Der Ausgang eines NFC-Transceiver-ICs ist typischerweise differenziell ausgeführt und erfordert eine symmetrische Beschaltung [4]](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1638971723-270-worpb0pyy.jpg.320x180.webp)
![Zum besseren Verständnis lässt sich die symmetrische Ausgangsschaltung (Bild 5) in eine äquivalente nicht-symmetrische NFC-Ausgangsschaltung überführen [4] Zum besseren Verständnis lässt sich die symmetrische Ausgangsschaltung (Bild 5) in eine äquivalente nicht-symmetrische NFC-Ausgangsschaltung überführen [4]](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1638971761-270-wor0cqdhb.jpg.320x180.webp)
![m Träger und zwei symmetrisch angeordneten Hilfsträgern [7]. m Träger und zwei symmetrisch angeordneten Hilfsträgern [7].](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1638971802-270-worrxmo6w.jpg.320x180.webp)
Zur Berechnung der Anpassungskondensatoren CA und CB können die Gleichungen 12 und 13 angewendet werden. Die Transformationsberechnungen werden auf der Basis des in [6] entwickelten Modells durchgeführt und die resultierende nicht-symmetrische Schaltung ist in Bild 5 dargestellt.
EMV-Filterschaltung
Da das Ausgangssignal des NFC-ICs eine rechteckige Form hat, müssen die Oberschwingungen herausgefiltert werden. Dies geschieht durch das EMV-Filternetzwerk, das einen Tiefpass zweiter Ordnung bildet. Der Tiefpassfilter besteht aus der Induktivität L0 und der Kapazität C0. Die Grenzfrequenz fC des EMV-Filters lässt sich mit Gleichung 14 berechnen.
Die Grenzfrequenz fC muss höher sein als der obere Hilfsträger, der für die höchstmögliche NFC-Datenrate (848 kbit/s) 13,56 MHz + 848 kHz = 14,4 MHz beträgt. Zur Veranschaulichung der Notwendigkeit des Filters ist in Bild 6 ein NFC-Lastmodulationsspektrum mit Träger und Hilfsträgern dargestellt
Um die Impedanzanpassung durchführen zu können, muss die Impedanz des Filters mit Gleichung 15 berechnet werden.
Impedanzanpassungsnetzwerk
Die Anpassungsschaltung, auch Impedanzanpassungsnetzwerk genannt, wie in den Bildern 4 und 5 gezeigt, hat zwei Aufgaben. Die erste ist die Kompensation der induktiven Impedanz der Antenne. Die zweite ist die Umsetzung der Impedanztransformation von der Lastimpedanz zur Quellenimpedanz. Für eine verlustfreie Transformation sollten alle Komponenten Blindwiderstände sein. In einer kosten- und platzkritischen Umgebung wie in NFC-Schaltungen ist es wünschenswert, die Anzahl der Komponenten auf ein Minimum zu beschränken, weshalb eine L-Schaltung für die Impedanzanpassung verwendet werden sollte.
Dämpfungswiderstände und äquivalente Antennenschaltung
Der Dämpfungswiderstand Rq ist ein optionaler Widerstand, der zur Reduzierung des Gütefaktors (Q-Faktors) der Antenne verwendet werden kann. Die Wahl des optimalen Werts für Rq ist ein Kompromiss. Auf der einen Seite erhöht ein kleiner Wert den Antennenwirkungsgrad der kontaktlosen Leistungsübertragung, auf der anderen Seite bietet ein hoher Widerstandswert eine höhere Bandbreite für die Modulation und verringert den Antennen-Q-Faktor. Der empfohlene Wertebereich für den Q-Faktor liegt zwischen 20 und 35, wie in [3] vorgeschlagen wird.
Der Widerstand Rq sollte eingesetzt werden, wenn der Q-Faktor der Antenne, der mit Gleichung 6 [5] berechnet werden kann, den Wert 35 überschreitet. Wenn der Wert höher ist, muss Gleichung 6 [5] mithilfe von Gleichung 16 modifiziert werden [4].
Daraus ergibt sich die folgende Formel zur Berechnung des Dämpfungswider-standswerts Rq für QL,mod ≥ 35:
Der letzte Teil des Ausgangsnetzwerks ist die äquivalente Antennenschaltung. Als NFC-Antenne wurde die Kombinationsspule WE-WPCC WPT/NFC von Würth Elektronik eiSos (Artikel 760308101312) gewählt.
![Parameter der äquivalenten Antennenschaltung (siehe Bild 3 in [5]) der NFC-Antenne WE-WPCC WPT/NFC von Würth Elektronik eiSos Parameter der äquivalenten Antennenschaltung (siehe Bild 3 in [5]) der NFC-Antenne WE-WPCC WPT/NFC von Würth Elektronik eiSos](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1638971878-270-worlucrcd.jpg.1280x0.webp)
Ihre Parameter (Tabelle 1) wurden durch Messung und Berechnung bestimmt. Die Werte für La und Ra wurden bei 13,56 MHz gemessen.
Bestimmung der komplexen Impedanz und des Q-Faktors
Die komplexe Impedanz ZL der gewählten NFC-Kombinationsspule wird mit Gleichung 5 [5] durch Einfügen der Parameter der äquivalenten Antennenschaltung berechnet, die im vorigen Abschnitt ermittelt wurden, und zu folgendem komplexen Impedanzwert führen: ZL = (1,87 + j 62,53) Ω. Dies führt aufgrund von Gleichung 6 [5] zu einem QL von 33. Da der Q-Faktor der Antenne kleiner als 35 ist, können die Dämpfungswiderstände Rq weggelassen werden.
Berechnung der Filterkomponenten und der komplexen Impedanz der Filterschaltung
Für die Grenzfrequenz fC, die mit Gleichung 14 berechnet werden kann, wurde ein Wert von 14,8 MHz gewählt, der höher als 14,4 MHz ist. Für L0 wird ein Induktivitätswert von 470 nH gewählt, was zu einem C0 von 247 pF führt. Die Werte L0 und C0 müssen in Gleichung 15 eingesetzt werden, um die komplexe Filterimpedanz zu berechnen. Für RD wird der Wert von 25 Ω eingefügt, der die differenzielle Ausgangsimpedanz eines typischen NFC-ICs in Bezug auf Masse ist.
Diese Werte führen zu der folgenden komplexen Filterimpedanz:
ZEMC = (165,82 – j 45,46) Ω
Berechnung der Werte der Anpassungskomponenten
Die Anpassungsreaktanzen XB und XA können direkt mit den Gleichungen 10 [5] und 11 [5] berechnet werden. Für RS muss der Realteil des EMV-Netzwerks eingesetzt werden, der 165,82 Ω beträgt. Für den Imaginärteil der Quellenreaktanz XS muss der Imaginärteil des EMV-Filters eingesetzt werden, der –45,46 Ω beträgt. Für RLund XLmüssen der Real- und der Imaginärteil des Antennennetzwerks integriert werden, nämlich 1,87 Ω und 62,53 Ω. Die resultierenden Anpassungsreaktanzen XA und XB können in die entsprechenden differenziellen Anpassungskondensatoren CA und CB folgendermaßen umgerechnet werden:
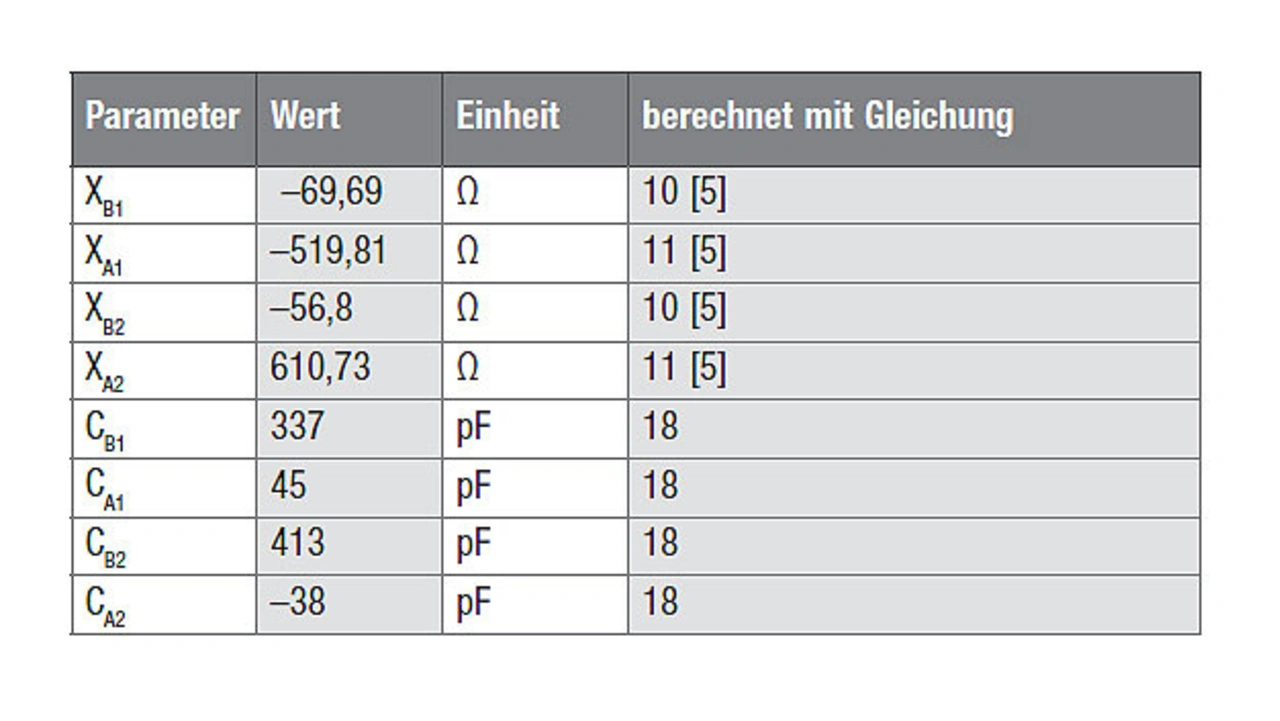
Tabelle 2 gibt einen Überblick über die resultierenden Reaktanz- und Kapazitätswerte. Die Kondensatorwerte für CA1 und CB1 werden für die Anpassung verwendet, die Werte für CA2 und CB2 werden vernachlässigt, da CA2 einen negativen Wert ergibt. Daraus ergeben sich die Anpassungskondensatoren für die symmetrische Ausgangsschaltung zu:
CA= 45 pF
CB= 337 pF
Berechnung des resultierenden Eingangsreflexionsfaktors
Um zu überprüfen, ob die berechneten Anpassungskondensatorwerte CA und CB zu einer niedrigen Reflexion führen, muss der Parameter S11 am Ausgang des NFC-ICs berechnet werden. Je kleiner die absoluten Werte sind, desto geringer ist die Reflexion und desto besser ist die Schaltung an die 50 Ω Ausgangsimpedanz des NFC-ICs angepasst. Der komplexe Eingangsreflexionsfaktor S11 kann mit Gleichung 19 berechnet werden.
In der Gleichung 19 ist RD = 25 Ω, was der nicht-symmetrischen Ausgangsimpedanz des NFC-ICs entspricht. Der Parameter Zin‘ hängt von der Eingangsimpedanz Zin ab (siehe Gleichung 7 [5]) und kann mit der Gleichung 20 berechnet werden.
Der Betrag von S11 kann berechnet werden mit:
In der Hochfrequenztechnik wird |S11| oft in einer logarithmischen Skala angegeben und kann wie folgt berechnet werden:
Die resultierenden Werte der Gleichungen 7 [5] sowie 19–22 sind in der Tabelle 3 zusammengefasst.
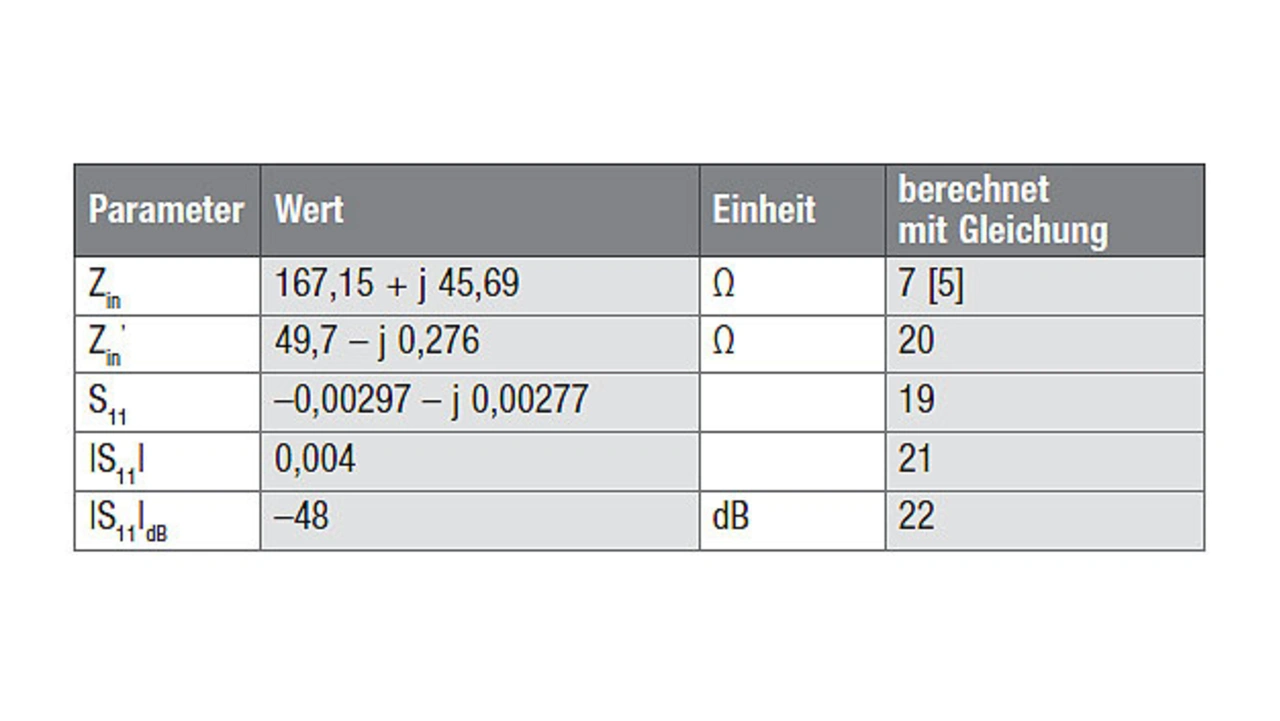
Die Berechnungen werden mit idealen Komponenten durchgeführt, ohne Berücksichtigung von Toleranzen und parasitären Einflüssen. In der Realität haben die Kondensatoren und Induktivitäten jedoch Toleranzen und parasitäre Induktivitäten und Kapazitäten. Zudem sind die Komponenten des Ersatzschaltkreises der Antenne gemessen und daher nicht sehr genau, haben also ebenfalls Toleranzen.
Neben geometrischen und chemischen Variationen, die durch den Herstellungsprozess verursacht werden, gibt es auch unbekannte Parameter der umgebenden oder zusätzlich angebrachten Ferritfolien zur Abschirmung. Jedes Metall in der Nähe der Antenne kann die Impedanz der Antenne und damit auch die gesamte Eingangsimpedanz verändern. Wie stark diese Variationen die Eingangsimpedanz beeinflussen, hängt hauptsächlich vom Wert der Eingangsimpedanz und dem Qualitätsfaktor ab. Im Allgemeinen sind niedrigere Qualitätsfaktoren und höhere Werte der Eingangsimpedanz weniger empfindlich auf eine Variation der Komponentenwerte [4]. Angesichts dieser Abweichungen ist eine zusätzliche Iteration der Anpassung notwendig.
Literatur
[5] Merz, C.: Near Field Communication: Impedanzanpassung für NFC-Anwendungen – Teil 1. Elektronik 2021, H. 24, S. 55–57.
[6] Schober, A.; Ciacci, M. und Gebhart, M.: An NFC Air Interface coupling model for Contactless System Performance estimation. 12th International Conference on Telecommunications (ConTEL), Konferenzband, 26.–28. Juni 2013, S. 243–250.
[7] Minihold, R.: Near Field Communication (NFC) Technology and Measurements. Rohde & Schwarz, White Paper, Juni 2011, https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/dl_application/application_notes/1ma182/1MA182_5E_NFC_WHITE_PAPER.pdf.
[8] Roland, M.; et. al.: Automatic Impedance Matching for 13.56 MHz NFC Antennas, 6th International Symposium on Communication Systems, Networks and Digital Signal Processing, Konferenzband, 23.–25. Juli 2008, S. 288–291.
[9] Khalid, M. A.; Mark, S. und Blakey, R.: WE-MCA Multilayer-Chipantenne Platzierung und Anpassung. Würth Elektronik eiSos, Application Note ANP057a, 19. September 2018, www.we-online.com/web/de/index.php/download/media/07_electronic_components/download_center_1/application_notes_berichte/anp057_we_mca_multilayer_chipantenne_platzierung_und_anpassung/ANP057a_DE2.pdf.
Der Autor

Christian Merz
geboren 1986, studierte Elektrotechnik an der Technischen Hochschule Deggendorf und schloss 2013 mit dem akademischen Grad Master of Science ab. Nach dem Studium arbeitete er als Wissenschaftlicher Mitarbeiter an der Technischen Hochschule Deggendorf zum Thema Energy Harvesting.
Seit Oktober 2018 ist er als Product Manager im Bereich Wireless Power Transfer (WPT) bei Würth Elektronik eiSos tätig. Bis heute veröffentlichte er insgesamt 17 Publikationen zu den Themen Energy Harvesting, Analyse nichtlinearer Schaltungen, Hochgüte-Impedanzanpassung und WPT/NFC.
Christian.Merz@we-online.de