Schaltungssimulation mit LTSpice
Unterschiede aufdecken
Fortsetzung des Artikels von Teil 3
Modifizierte Gear-Integration
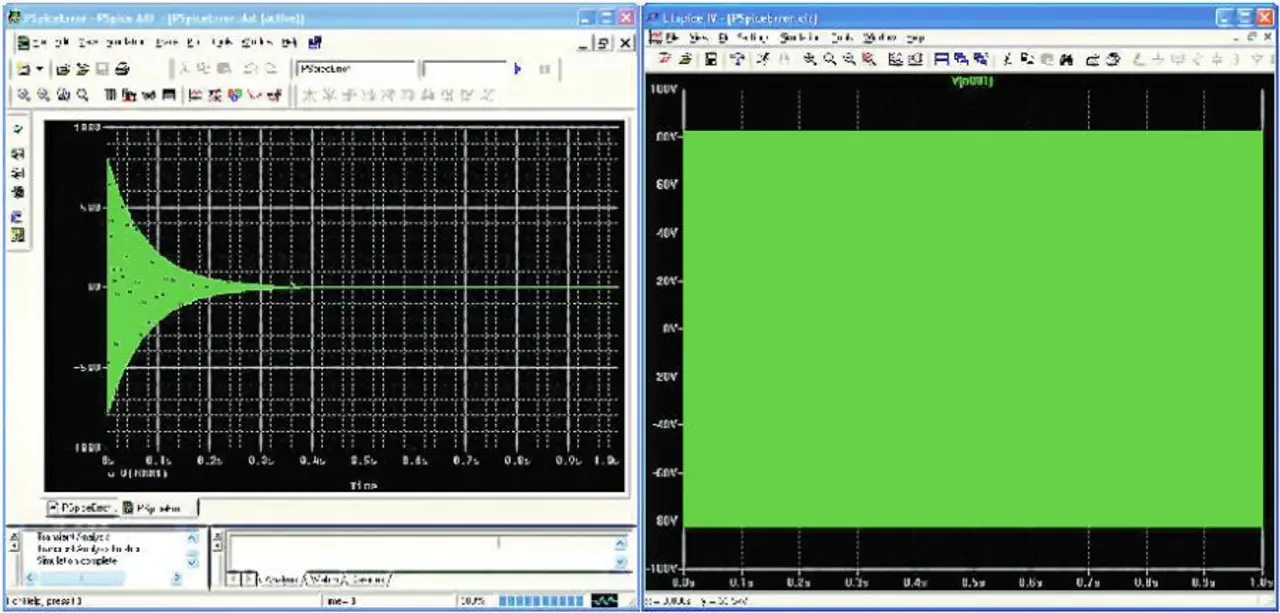
Bild 3 zeigt, dass die modifizierte Gear-Integration das Schwingen künstlich dämpft, wohingegen LTSpice sofort die korrekte Lösung findet. Der Fehler in PSpice kann durch Festsetzen eines kleineren maximalen Zeitschritts (vierte Zahl im „.tran statement“) reduziert werden. Dies ist eine relativ einfache Schaltung, die für die Berechnungen mit dem modifizierten Gear von PSpice herangezogen wurde.
Eine Schaltung mit vielen unterschiedlichen Zeitkonstanten ist zwangsläufig nicht für PSpice geeignet, will man zuverlässige Analysen erhalten. Es ist kein guter Weg, wenn der Ingenieur nachträglich manuell dahingehend überprüfen muss, ob sich seine Simulation durch noch kleinere maximale Zeitschritte der realen Lösung annähert.
Jobangebote+ passend zum Thema
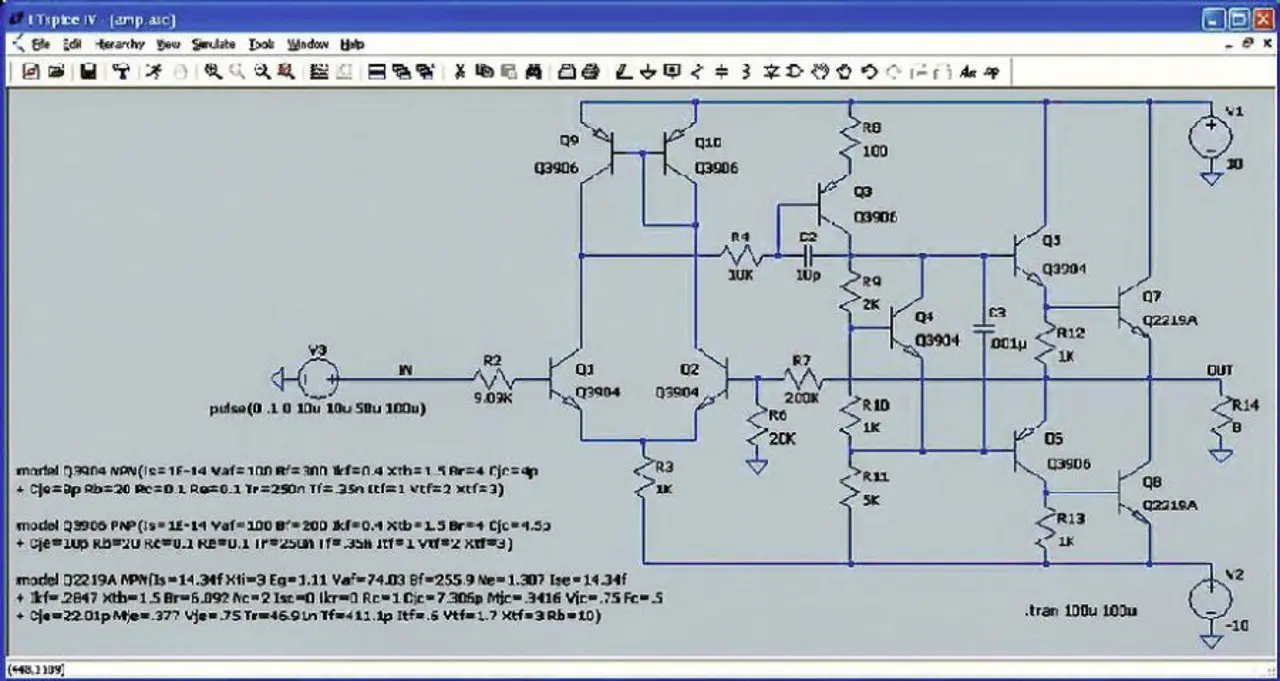
Bild 4 zeigt ein weiteres interessantes Beispiel: einen Audio-Leistungsverstärker, der nicht stabil ist, weil der Kompensationskondensator C2 zu klein ist. PSpice simuliert diese Schaltung als stabil, wohingegen LTspice das korrekte Ergebnis ausgibt. Die in diesem Fall verwendete Netzliste ist in Listing 3 festgehalten:
- Unterschiede aufdecken
- 2. Methode: Sparse-Matrix-Methoden
- 3. Methode: Implizite Integration
- Modifizierte Gear-Integration
- Ein fälschlicherweise stabiles Ergebnis
- Zusatzinformationen
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Point-of-Load-Wandler
Thermische Probleme gelöst
Community-orientiertes Internetportal
Zugriff auf Analog- und Mixed-Signal-Simulations-Tools
Linear Technology
LTPoE++-PD-Controller mit Fluss-/Sperrwandler-Controller
Spannungsregler
LT3959 von Linear Technology für Eingangsspannungsbereich von 2,5 – 40 V
HV-Dioden-Controller
LTC4359 von Linear Technology ersetzt Schottky-Dioden
DCR-Messung ab 0,17 mΩ
Linear Technology: Neuartige Architektur für CM-DC/DC
