Schaltungssimulation mit LTSpice
Unterschiede aufdecken
Der Beitrag liefert anhand einfacher Beispiele verschiedene Argumente, weshalb das „LT“-Derivat des Berkeley-Spice-Simulators bessere Ergebnisse erzielt als die am Markt verfügbaren Wettbewerber.
Entwicklungsingenieure für analoge Schaltungen verlassen sich stark auf die Simulation, um das Verhalten ihrer Designs bestimmen zu können. Der Wert der Simulation hängt davon ab, wie gut diese die physikalischen Gegebenheiten vorhersagt und wie schnell sie Ergebnisse erbringt. Gibt es größere Diskrepanzen zwischen dem simulierten und dem realen Verhalten, so wird der Entwickler diese Schaltung noch mit kostenintensiven Debugging-Zyklen verifizieren müssen.
Spice wird für die Simulation analoger Schaltungen benutzt, weil es das Großsignalverhalten von beliebigen Schaltungen berechnen kann. Für den Erfolg von Spice bei der Simulation von analogen Schaltungen sind drei numerische Methoden verantwortlich:
- Die Newton-Iteration, um eine Lösung für Schaltungen mit nichtlinearen Elementen zu finden
- Sparse-Matrix-Methoden, um riesige Matrizen im Adressbereich eines geeigneten Computers ablegen zu können
- Die implizite Integration, um jene differenziellen Gleichungen integrieren zu können, welche von Schaltungs-Blindwiderständen hervorgerufen werden
Die Fähigkeit eines Spice-Simulators, zuverlässig korrekte Ergebnisse zu generieren, hängt wesentlich davon ab, wie gut diese Methoden implementiert sind. Die folgenden Ausführungen liefern Argumente, warum LTSpice besser bei der Generierung korrekter Ergebnisse ist als andere Spice-Implementierungen.
Jobangebote+ passend zum Thema
1. Methode: Newton-Iteration
Die Newton-Iteration bedeutet das Ausweiten der I-U-Kurve jedes nichtlinearen Schaltungsteils in eine Taylor-Serie, behält davon aber nur die ersten beiden Terme und löst das resultierende System von linearen Gleichungen. Wenn die Lösung des linearen Systems der Punkt ist, an dem die Taylor-Reihe entwickelt wurde, dann ist die Lösung dieses linearen Systems die korrekte Lösung für die ursprüngliche nichtlineare Schaltung [1]. Dies gilt, weil die Taylor-Näherung an diesem Punkt exakt ist.
Die Robustheit der Newton-Iteration hängt allerdings von zwei Kriterien ab:
- Die I-U-Kurven aller Schaltungselemente müssen in Wert und Ableitung kontinuierlich sein.
- Alle nichtlinearen Elemente müssen mit Kondensatoren überbrückt sein, sodass die Lösung des vorherigen Zeitschritts ein guter Startpunkt für die Newton-Iteration des aktuellen Zeitpunkts ist.
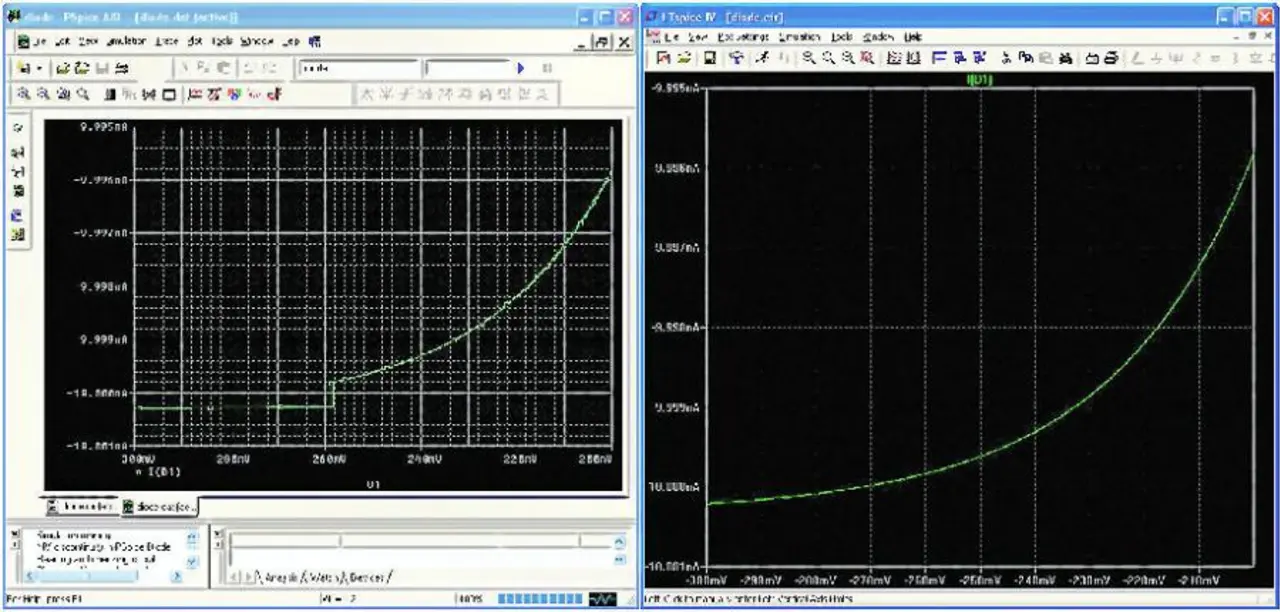
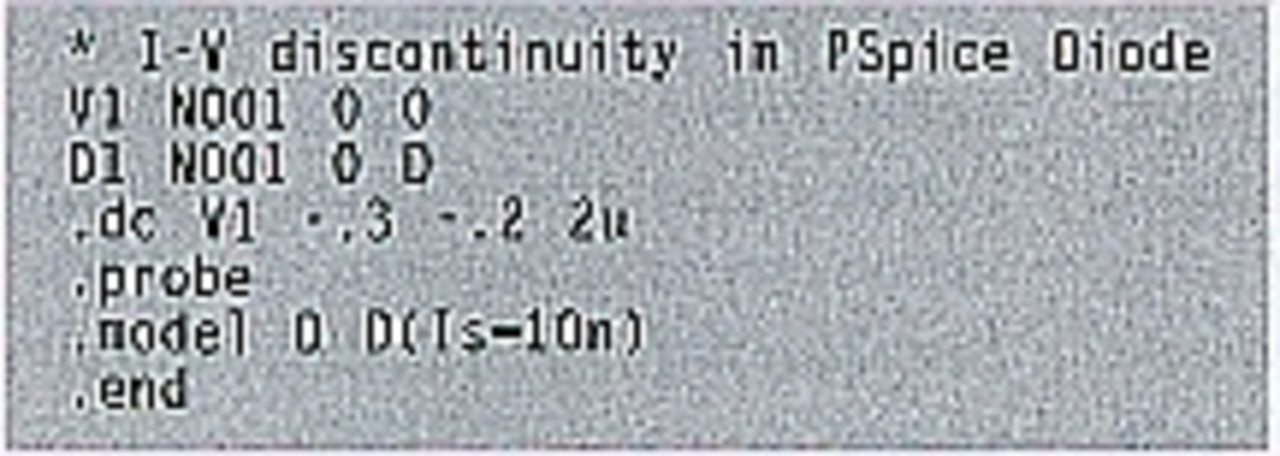
Beide Bedingungen werden von jeder physikalischen Schaltung erfüllt, aber Spice-Programme können das üblicherweise nicht richtig abbilden, weil die in Berkeley-Spice modellierten Halbleiterbauelemente Unstetigkeiten aufweisen und diese Implementierungsfehler sich in käuflichen Spice-Implementierungen wiederfinden. Diese Unstetigkeiten treten in LTSpice, das für Linear Technology entwickelt wurde, indes nicht auf. Bild 1 zeigt beispielhaft die I-U-Kurve einer Diode in PSpice [2] und LTSpice. Die hierbei verwendete Netzliste ist in Listing 1 wiedergegeben. Die I-U-Kurve der PSpice-Diode weist – siehe Bild 1 links – eine Unstetigkeit auf.
- Unterschiede aufdecken
- 2. Methode: Sparse-Matrix-Methoden
- 3. Methode: Implizite Integration
- Modifizierte Gear-Integration
- Ein fälschlicherweise stabiles Ergebnis
- Zusatzinformationen
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Point-of-Load-Wandler
Thermische Probleme gelöst
Community-orientiertes Internetportal
Zugriff auf Analog- und Mixed-Signal-Simulations-Tools
Linear Technology
LTPoE++-PD-Controller mit Fluss-/Sperrwandler-Controller
Spannungsregler
LT3959 von Linear Technology für Eingangsspannungsbereich von 2,5 – 40 V
HV-Dioden-Controller
LTC4359 von Linear Technology ersetzt Schottky-Dioden
DCR-Messung ab 0,17 mΩ
Linear Technology: Neuartige Architektur für CM-DC/DC
