Startseite > Halbleiter > Design > Unterschiede aufdecken

Schaltungssimulation mit LTSpice

Unterschiede aufdecken

5. August 2015, 13:25 Uhr | Von Mike Engelhardt

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 2

3. Methode: Implizite Integration

Die Simulation analoger Schaltungen erfordert eine numerische Integration von Differenzialgleichungen, um das Verhalten der Kondensatoren und Spulen nachverfolgen zu können. Hier sind die größten Unterschiede zwischen den einzelnen Spice-Implementierungen erkennbar, und zwar hinsichtlich der Methoden, die für das Integrieren bzw. Lösen der Differenzialgleichungen zur Verfügung stehen.

Jede numerische Integration ist fehlerbehaftet: Beim Integrieren von Differenzialgleichungen, welche Lösungsterme der Form x^{(–const × time)} aufweisen, summieren sich die Fehler auf, wenn nicht eine numerische Methode – die sogenannte implizite Integration – Anwendung findet [5]. Ohne implizite Integration wäre eine Transientenanalyse in Spice nicht möglich.

Spice nutzt Integration zweiter Ordnung. Die meisten Spice-Implementierungen orientieren sich an Berkeley-Spice und verwenden zwei verschiedene Arten der implizierten Integration 2. Ordnung: „Gear“ und „Trapezoid (Trap)“ [6]. Die Trap-Integration ist sowohl schneller als auch genauer als die Gear-Integration. Allerdings kann sie numerische Artefakte hervorrufen, wobei die verwendete Lösung mit diskreten Zeitschritten von Zeitschritt zu Zeitschritt um das wahre kontinuierliche Zeitverhalten herum oszilliert. Dies kann den Nutzer dazu veranlassen, an der Korrektheit des Simulators zu zweifeln, obwohl jedes Trapezoid den korrekten „integrierten Bereich“ enthält.

Bei manchen Entwicklern von analogen Schaltungen fehlt die Akzeptanz für das zyklische Trap Ringing, sodass die Trap-Integration aus der kommerziellen Spice-Implementierung PSpice entfernt wurde und damit die langsamere und weniger genaue Gear-Integration als alleinige Option übrig blieb.

Die Gear-Integration dämpft aber nicht nur das numerische Schwingen – sie dämpft jegliches, auch physikalisch begründetes Schwingen. Als Folge kann eine Schaltung trotz vorhandener Oszillationen im realen Betrieb während der Simulation als perfekt stabil bewertet werden, weil diese Instabilität aus der numerischen Existenz weggedämpft wurde. Dies hat schon zur desaströsen Situation geführt, dass ein IC-Design in PSpice simuliert, layoutet und hergestellt wurde und man später erst herausfand, dass diese Schaltungen aufgrund einer Instabilität , welche durch das Gear-Verfahren in Spice übersehen wurde, nicht funktionierte.

Prinzipiell könnte der Gear-Integrations-Fehler reduziert werden, indem der IC-Designer einen kleinstmöglichen maximalen Zeitschritt festlegt. Dies ist jedoch keine geeignete Lösung, weil kleine Zeitschritte die Simulationsgeschwindigkeit auf ein Kriechen verlangsamen und es keinen Weg gibt, sicherzustellen, dass dieser Zeitschritt klein genug ist.

Die Dokumentation von PSpice erwähnt, dass eine modifizierte Gear-Methode verwendet wird und deshalb tatsächlich besser funktioniert als die Implementierung der Gear-Integration in Berkeley-Spice. Offensichtlich wird ein genügend kleiner Zeitschritt verwendet, der den Fehler als solches reduziert.

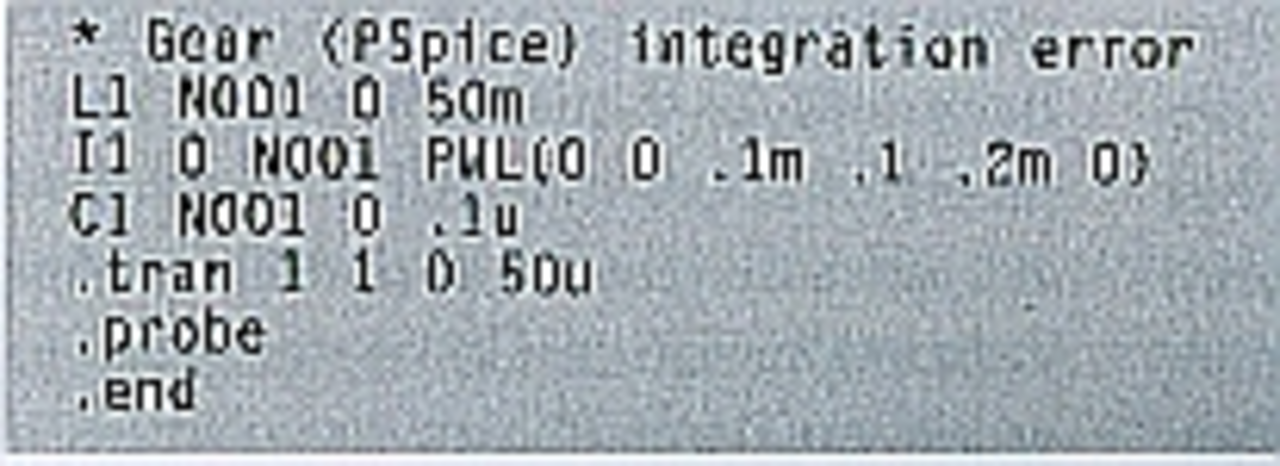
Die Methode von PSpice versagt jedoch häufig. Es ist einfach, eine triviale Schaltung zu erstellen und zu sehen, wie die Lösung von PSpice von der offensichtlich richtigen Lösung abweicht. Bild 2 zeigt einen parallelen Schwingkreis mit einer parallelen, stückweise linearen Stromquelle. Diese Stromquelle generiert eine Stromspitze binnen der ersten 0,2 ms und ist danach Null. Die Lösung sollte sein, dass der Parallelschwingkreis mit der Eigenfrequenz angeregt wird und danach mit einer konstanten Amplitude schwingt. Die Netzliste für diese Schaltung ist in Listing 2 festgehalten.