LTspice-Makromodelle für Analogschalter
Das Erstellen eigener SPICE-Modelle ist nicht schwer
Fortsetzung des Artikels von Teil 1
Modellparameter ermitteln
Modellparameter für die Ladungsinjektion
Wenn MOS-Transistoren abschalten, muss die Ladung im Kanal irgendwo hinfließen, so dass sie aus den Drain- und Source-Anschlüssen austritt. Wenn ein Analogschalter ausgeschaltet wird, tritt auch Ladung aus, was als Ladungsinjektion bezeichnet wird. Eine gebräuchliche Art, diese zu messen, besteht darin, an einem Ende eines Einschalters eine feste Spannung und am anderen Ende einen großen Kondensator anzulegen. Beim Ausschalten wird die Ladung vom Kondensator aufgenommen und es entsteht eine kleine Spannungsänderung.
Jobangebote+ passend zum Thema
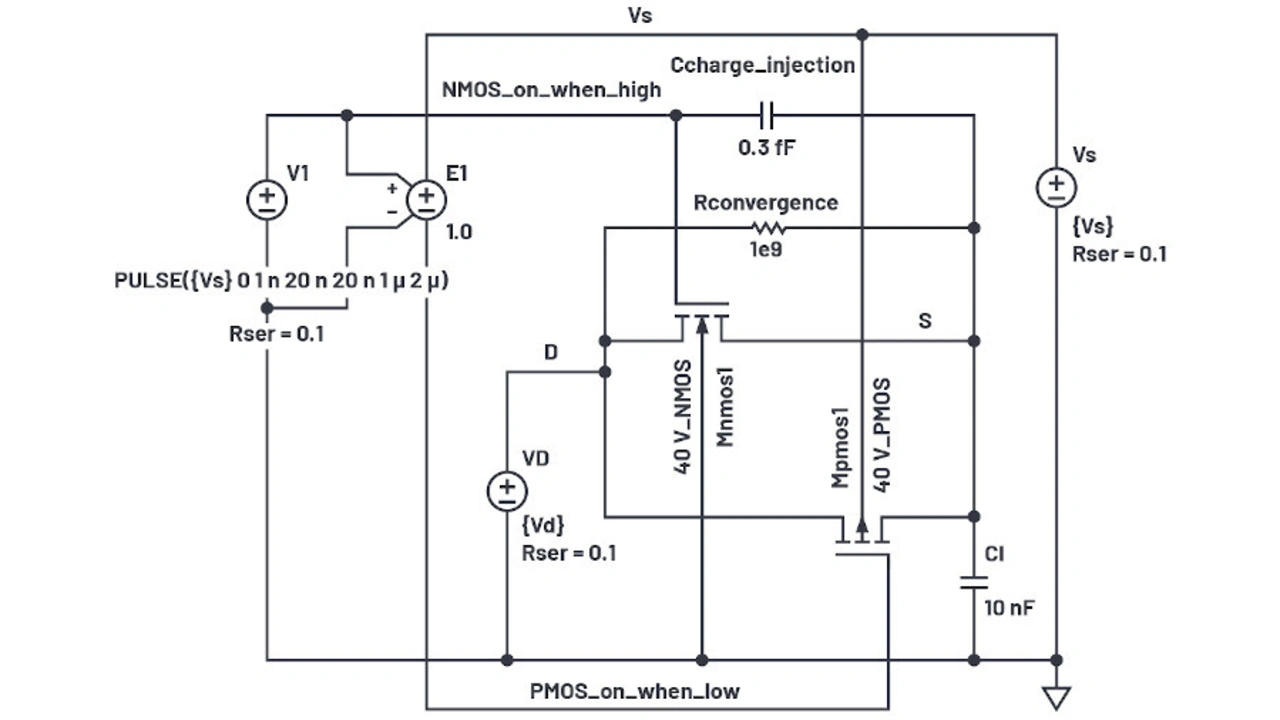
Für die Simulation wird nun die Gate-Oxiddicke TOX = 1 × 10–7 zu den MOS-FET-Modellen hinzugefügt – die Gate-Kapazität ist die größte Quelle der Ladungsinjektion. In der neuen Simulationsschaltung in Bild 9 ist nun die Stromquelle (Itest, Bild 2) durch die Kapazität Ccharge_Injection ersetzt.
Bei der Testschaltung für die Ladungsinjektion im Datenblatt wird eine Spannungsquelle (VD) am Anschluss D und ein Kondensator (Cl) am Anschluss S des Analogschalters platziert. Wenn die Schalter-FETs abgeschaltet werden, wird Cl isoliert und nimmt die von den Schaltern zugeführte Ladung auf. Die Wellenform eines solchen Ereignisses mit auf 24 V gehaltener Spannung am Anschluss D bei einer 30-V-Versorgung ist in Bild 10 dargestellt.
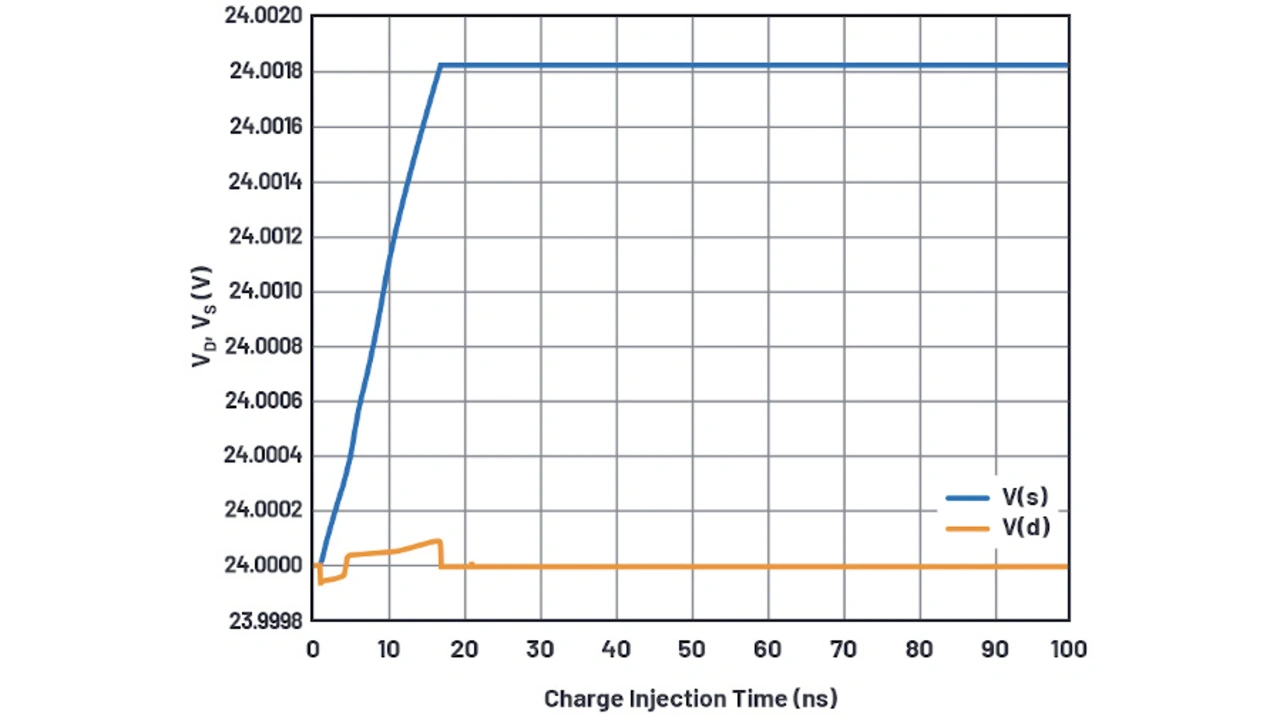
Die injizierte Ladung entspricht dem Spannungssprung zwischen der Spannung am Anschluss S und der Spannung am Anschluss D multipliziert mit dem 10-nF-Haltekondensator. Um den Wert der Ladungsinjektion bei jeder Spannung zu erfassen, kann die Schaltspannung für den Anschluss D über die Versorgungsspannung stufenweise erhöht werden, mit der meas-Anweisung. Im Bild 11a ist das Simulationsergebnis dargestellt, im Vergleich zur Datenblattkurve (Bild 11b).
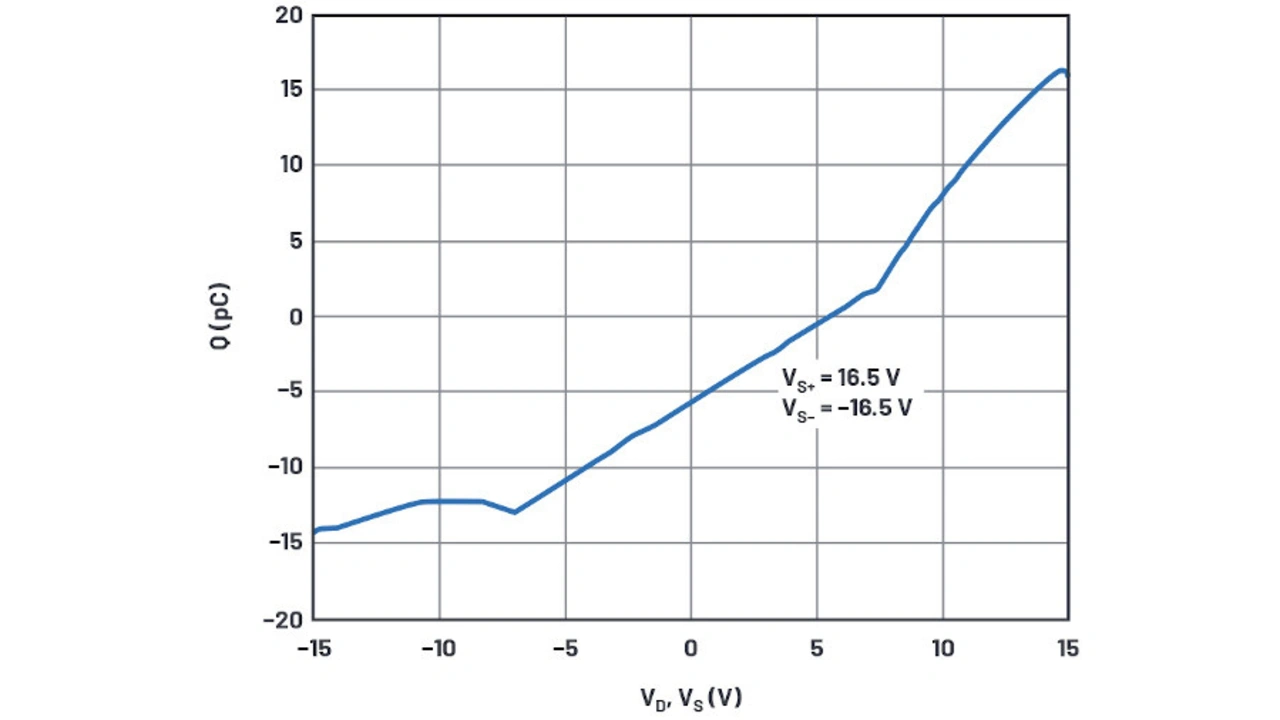
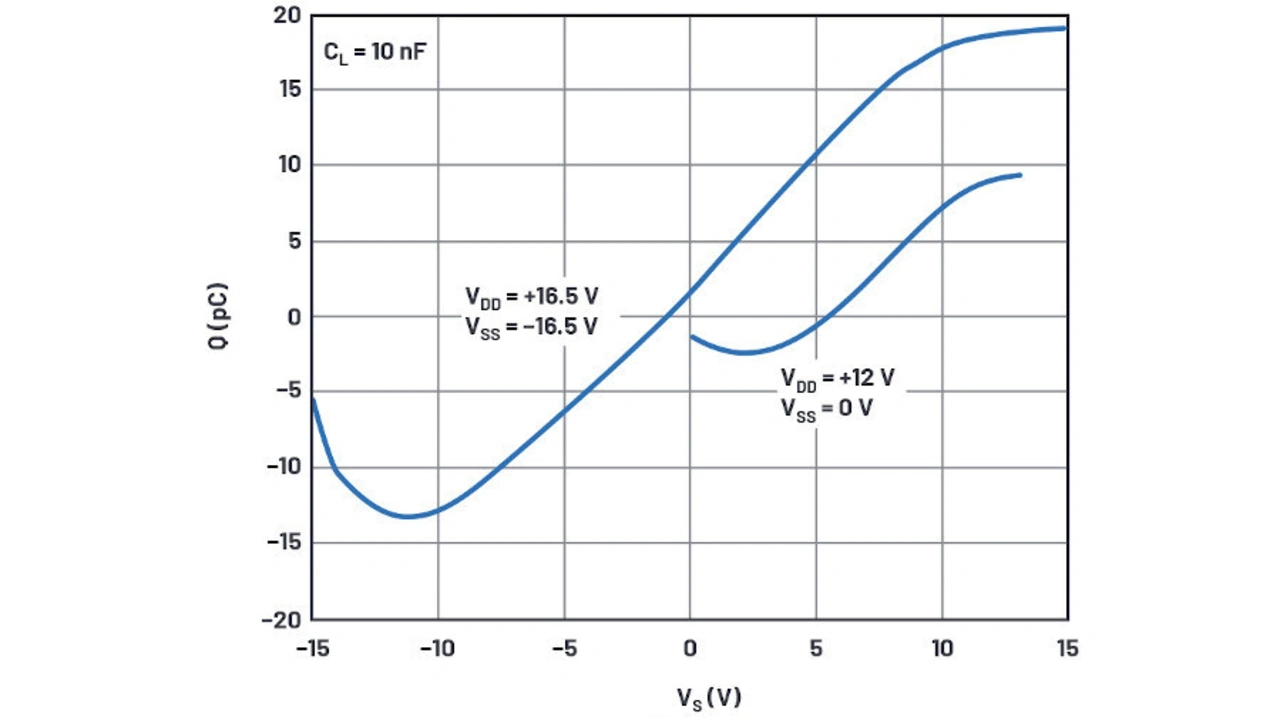
Das einfache MOS-Modell bildet die Form der Datenblattkurve nicht sehr gut nach, aber die Spitze-Spitze-Ladung beträgt 32 pC in den Datenblattkurven und 31 pC in der Simulation. Dies ist schon überraschend nahe dran, aber wenn es sein müsste, könnte die Gate-Oxiddicke (TOX) noch optimiert werden, um das Simulationsergebnis zu perfektionieren.
Zwischen den Kurven (Bild 11a und 11b) besteht ein Versatz, der sich mit CCHARGE_INJECTION ausgleichen lässt. Das Experimentieren mit einigen Werten ergibt CCHARGE_INJECTION = 0,28 pF als optimalen Wert. Wenn eine Verschiebung mit entgegengesetzter Polarität erforderlich wäre, müsste die Kapazität CCHARGE_INJECTION mit dem Knoten PMOS_on_when_low verbunden werden.
Der zur Anpassung eingefügte Kondensator CCHARGE_INJECTION stellt eine einfache Möglichkeit dar, um in der Simulation die Ladungsinjektion gegenüber der analogen Spannung auszugleichen. Was wäre, wenn die simulierte Spitze-Spitze-Ladung zu klein wäre? Nun, der größte Teil der Ladungsinjektion besteht zumeist aus den Schwankungen der Gatespannung der Analogschalter, die dazu führt, dass Ladung durch die Gate-Kapazität der MOSFETs verschoben wird.
Würde das Modell eine zu geringe Injektion simulieren, lässt sich einfach ein oder beide Gate-Bereiche vergrößern. Dazu müssten die Parameter L und W eines MOSFETs um den gleichen Faktor erhöht werden, wobei darauf zu achten ist, dass das W/L-Verhältnis, das den Ein-Widerstand festlegt, nicht verändert wird. Anstatt CCHARGE_INJECTION zu verwenden, hätten auch die Werte W und L des NMOSFET erhöht werden können.
Alternativ könnten der Wert für TOX in jedem Bauteil angepasst werden, um eine bessere Korrelation der Ladungsinjektion zu erhalten. Das wäre physikalisch nicht möglich – aber es ist ja auch nur eine Simulation. Bei den einfachen Modellen, die hier verwendet werden, beeinflusst TOX andere Schaltungsverhalten nicht.
Modellparameter für Kapazitäten
Mit den optimierten Parametern für REin und die Ladungsinjektion für gute Simulationsergebnisse, erfolgt als nächstes die Simulation der Kapazitäten der Anschlüsse S und D.
Ein wichtiger Punkt ist, dass sowohl der Drain- als auch der Source-Bereich von MOSFET-Schaltern für hohe Spannungen Driftbereiche aufweisen müssen. Als Schalter lässt sich der funktionelle Unterschied zwischen Source- und Drain-Anschlüssen nicht erkennen, und das Substrat-Potential gegenüber den Drain- und Source-Anschlüssen erfordert die entsprechenden Driftregionen in beiden. Dies gilt auch für die Soft-Diffusionen im mittleren Spannungsbereich, die jedoch bei Kleinspannungs-MOSFETs nicht vorhanden sind. Der verteilte Widerstand der Driftregion, der sowohl im Drain als auch in der Source vorhanden wäre, lässt sich in RD zusammenfassen, was bei Schaltern gut funktioniert, jedoch nicht bei Transistoren in der Sättigung. Bild 12a zeigt die für die Simulation der Kapazitäten geänderte Schaltung.
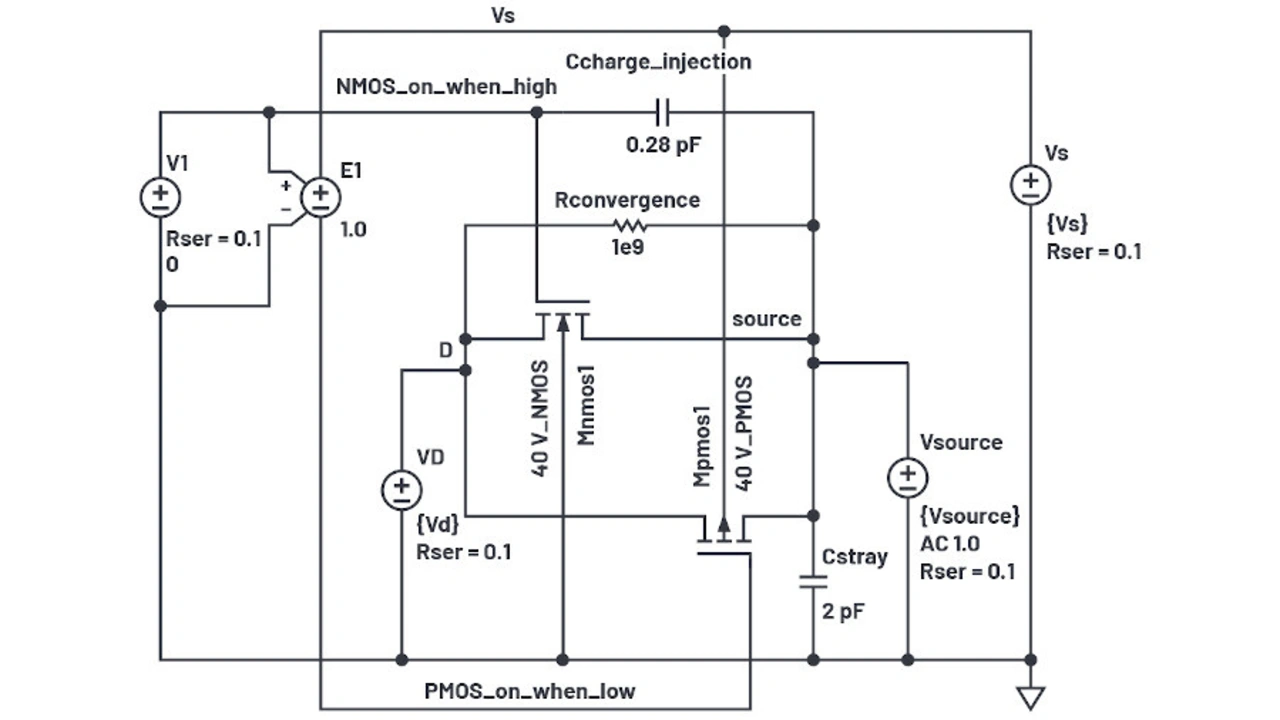
In LTspice lässt sich eine .ac-Analyse nur auf einer Frequenz ausführen, indem die Listenoption in .ac verwendet und dabei aber nur ein Frequenzargument angegeben wird, hier 1 MHz. Anschließend wird eine .step-VSOURCE-Gleichspannung über den Versorgungsspannungsbereich variiert, um einen Verlauf der Kapazität gegenüber der Spannung zu erhalten.
Der D-Anschluss des Ausschalters wird auf mittlerer Versorgungsspannung gehalten. Der S-Anschluss, der hier zur Vermeidung von Verwechslungen mit der Versorgungsspannung (VS) in Source umbenannt wurde, wird von einer Gleichspannungsquelle angesteuert. Sie überstreicht den Bereich von 0 V bis zur Höhe der Versorgungsspannung und wird über eine Wechselspannung von 1 V gesteuert. Die Kapazität wird von I(VSOURCE)/(2 × π × 1 MHz × 1 V) abgeleitet. Die Logikansteuerung V1 wird auf 0 V geändert, um die MOSFETs auszuschalten.
Die Drain- und Source-Kapazitäten zum Substrat (Bulk) werden in der Modellerklärung als CBD bzw. CBS bezeichnet. Das Modell verfügt über eingebaute Standardkonzentrationen, eine interne Spannung und einen Exponenten, die CBD und CBS spannungsabhängig machen. Da diese symmetrisch sind, würden die Drain- und Source-Kapazitäten gleichgesetzt werden. Da der PMOSFET eine andere Kanalbreite als der NMOSFET hat, ist darüber hinaus das Verhältnis von CBD,NMOS/CBD,PMOS = CBS,NMOS/CBS,PMOS = WN/WP, das bereits bei der Modellierung des Ein-Widerstands ermittelt wurde.
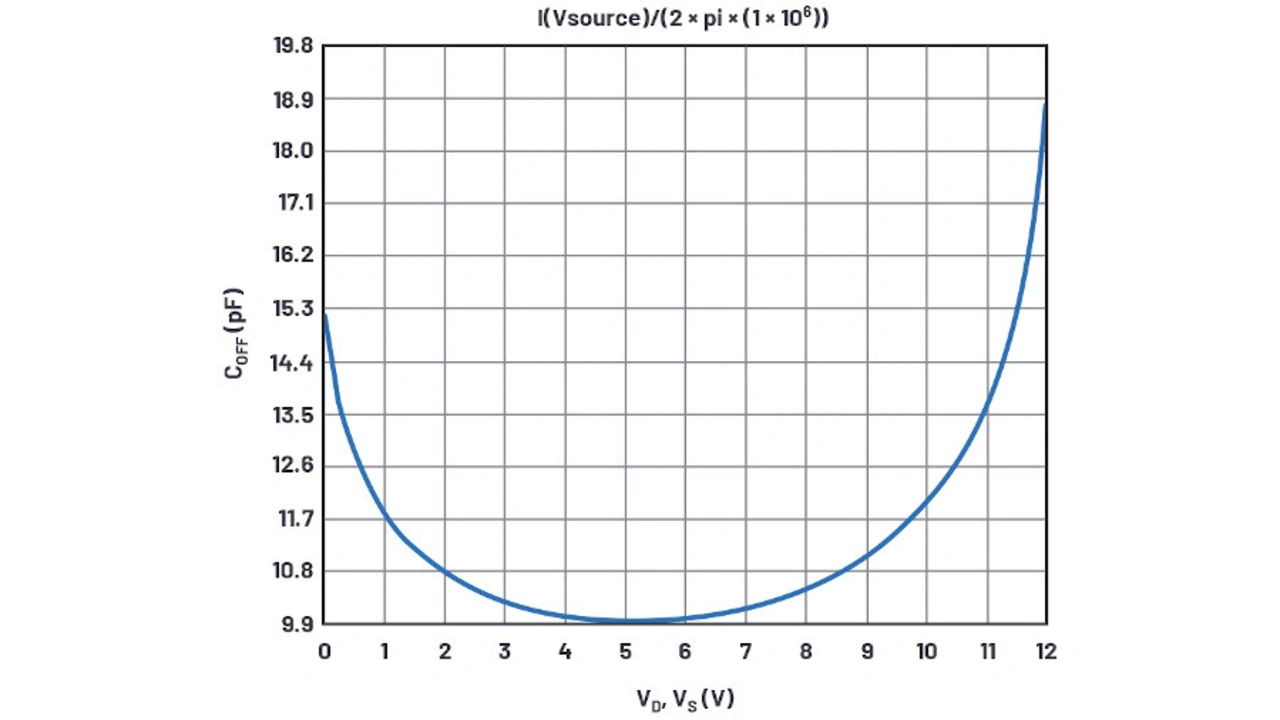
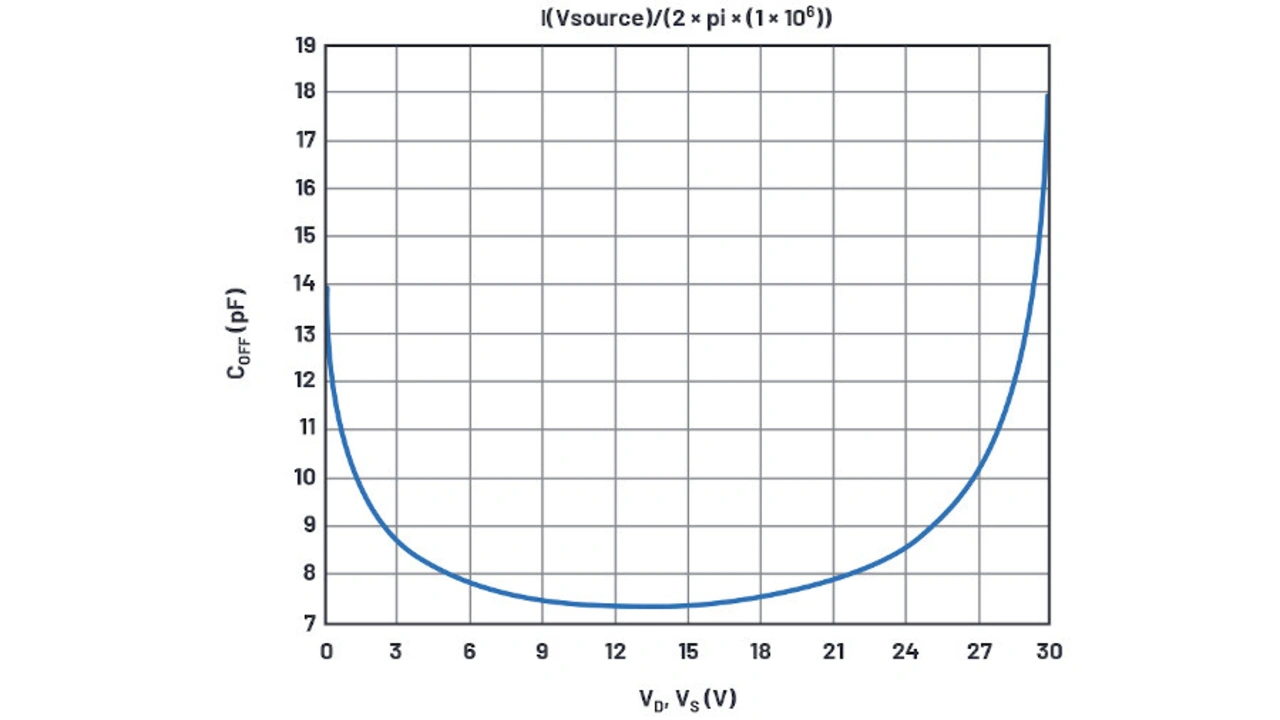
Die Bilder 13a und 13b zeigen die Simulationsergebnisse für I(VSOURCE)/(2 × π × 1 MHz), was eine Kapazität darstellt. LTspice weiß dies allerdings nicht und zeigt pA statt pF an.
Leider enthält das Datenblatt [2] keine Diagramme, die einen Vergleich erlauben. In der Spezifikationstabelle im Datenblatt ist Kapazität – CS (OFF) genannt – mit typischen Werten genannt: 7 pF bei einer Versorgungsspannung von 30 V und 12 pF bei Versorgungsspannung von 12 V. Diese Werte beziehen sich wahrscheinlich auf die Mitte der jeweiligen Versorgungsspannung, dies ist jedoch nicht im Datenblatt angegeben. Im nächsten Schritt wurden die CBs angepasst, um die 7 pF-Kurve bei 30 V zu erhalten, aber nur 10 pF bei einer 12-V-Versorgung simuliert. Experimente mit dem internen Potenzial und dem Exponenten der Kapazitätsformel zeigen, dass das verwendete Modell keine Möglichkeit bietet um die 12 V/30 V-Übereinstimmung zu verbessern.
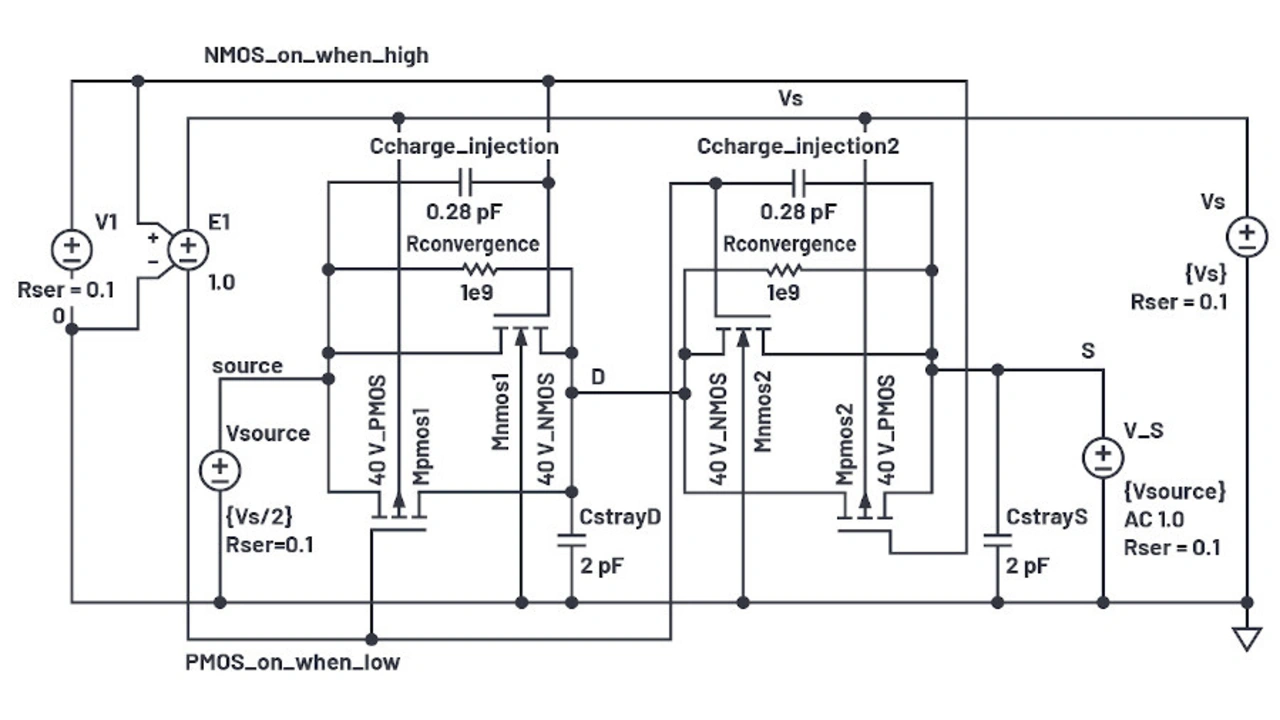
In der Schaltung in Bild 14a ist der rechte Schalter eines Wechselschalters eingeschaltet, während der linke Schalter ausgeschaltet und an eine VS/2-Quelle angeschlossen ist. Die Kapazitäten der rechten Hälfte des linken Schalters und die Kapazitäten des rechten Schalters sowie die unvermeidlichen parasitären Kapazitäten an den Anschlüssen D und S werden alle parallel geschaltet und von dem 1-MHz-Testsignal an der VS-Quelle angesteuert, deren Gleichspannungspegel von Masse bis VS gestuft ist.
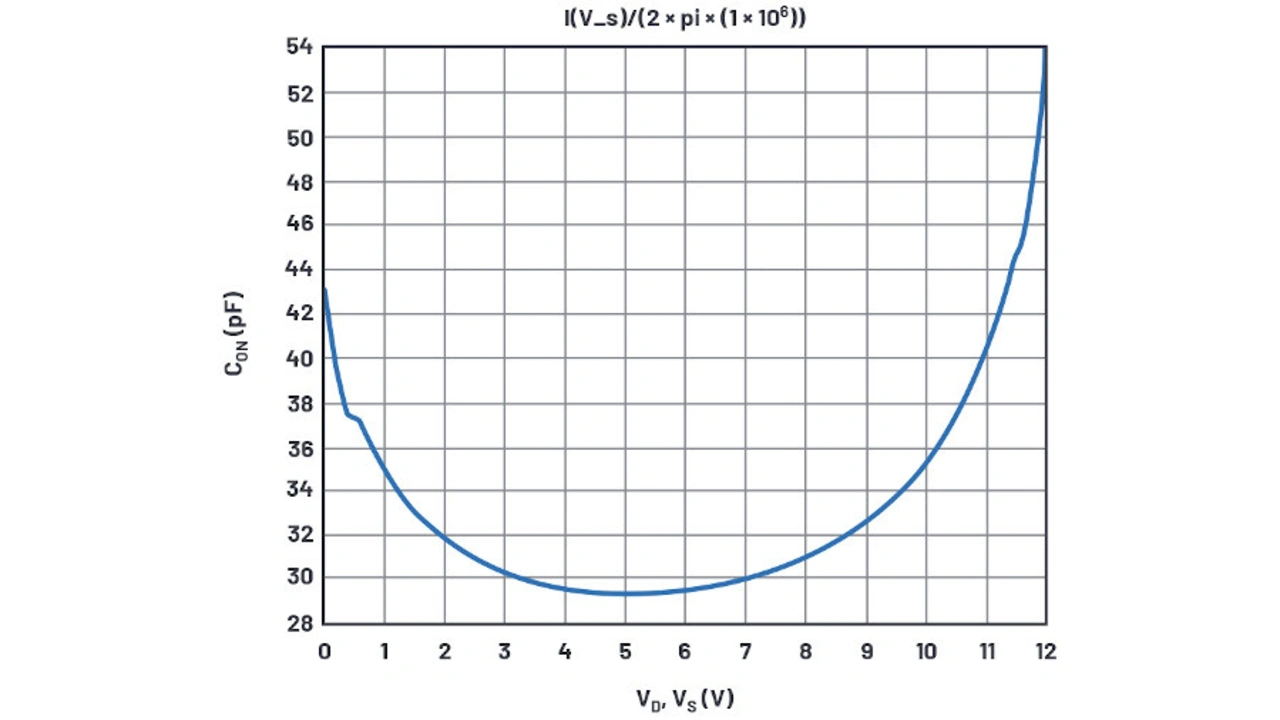
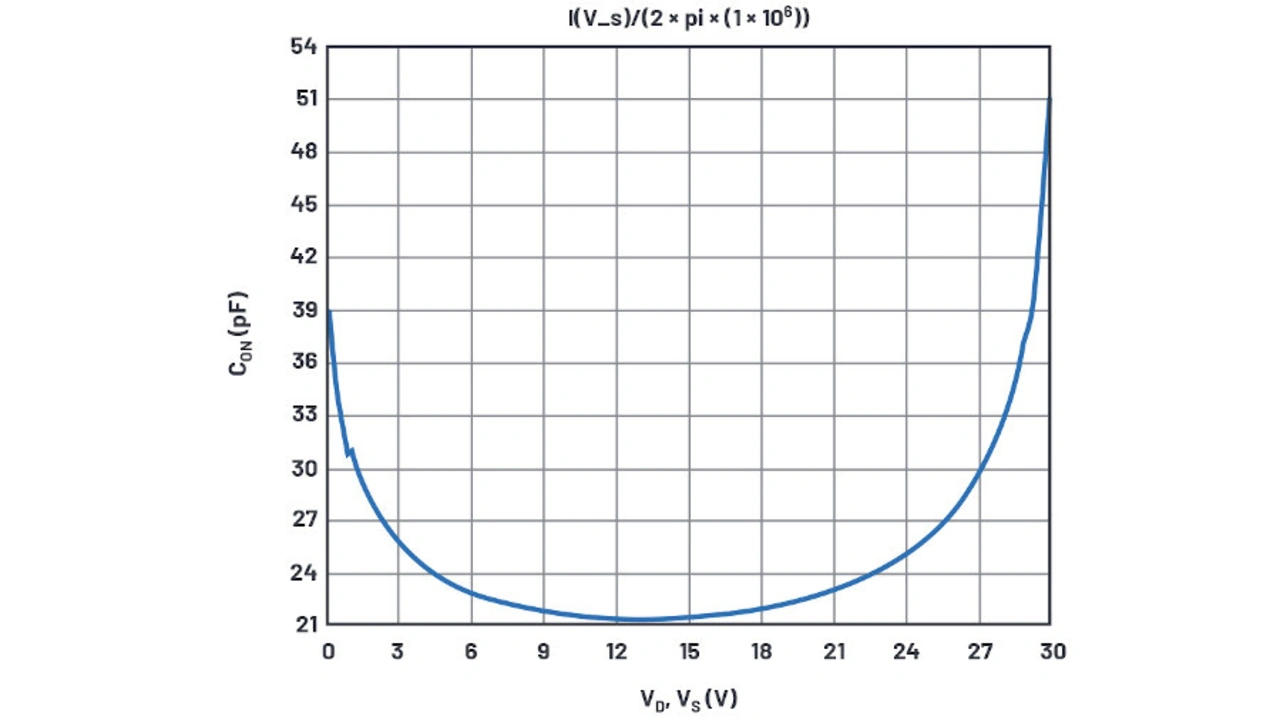
Die Ergebnisse der Simulation für die Ein-Kapazität (Bilder 15a und 15b) ergeben 29,5 pF bzw. 21,4 pF, wogegen im Datenblatt 26 pF bzw. 25 pF angegeben sind. Angesichts der üblichen Kapazitätsschwankungen von Leiterplatten-Layouts lassen sich die in der Simulation ermittelten Werte als nahe genug an der Realität betrachten.
Leckströme
Im Datenblatt [2] sind Diagramme abgebildet, die bei 25 °C spannungsabhängige Leckströme im pA-Bereich zeigen. Demgegenüber werden in den Spezifikationen des Datenblatts lediglich Leckströme im Bereich von einigen hundert pA garantiert. Die in den Diagrammen gezeigten Ergebnisse bei 25 °C überzeugen mehr. Die geringen Leckströme wurden bei diesem Analogschalter-IC offenbar nicht für wichtig genug gehalten, um sie durch Tests zu garantieren. Fairerweise muss man sagen, dass die Messung von Stromstärken im einstelligen pA-Bereich einen hohen technischen Aufwand und lange Testzeiten erfordert.
Bei 85 °C werden einige nA garantiert – die effizient gemessen werden können – mit einem typischen Ergebnis im Bereich von einigen hundert pA. Diese typischen Ergebnisse lassen sich als gut akzeptieren.
Die Leckströme sind ein Produktmangel; es gibt diesbezüglich keine genauen Statistiken und sie schwanken stark mit der Temperatur. Es ist nicht die Art von Spezifikation, nach der Entwickler einen Schaltungsentwurf ausrichten – vielmehr ist es eine Größe, die die Schaltkreise stört, mit denen der Analogschalter verbunden ist. Bei der Verwendung von Makromodellen werden sämtliche Leckströme von signifikanter Größe als Schaltungsdefekte simuliert, was eine nützliche Warnung für den Entwickler darstellt. Für die Simulation wird ein Zielwert von 1 nA für einen Schließer bei 85 °C gewählt.
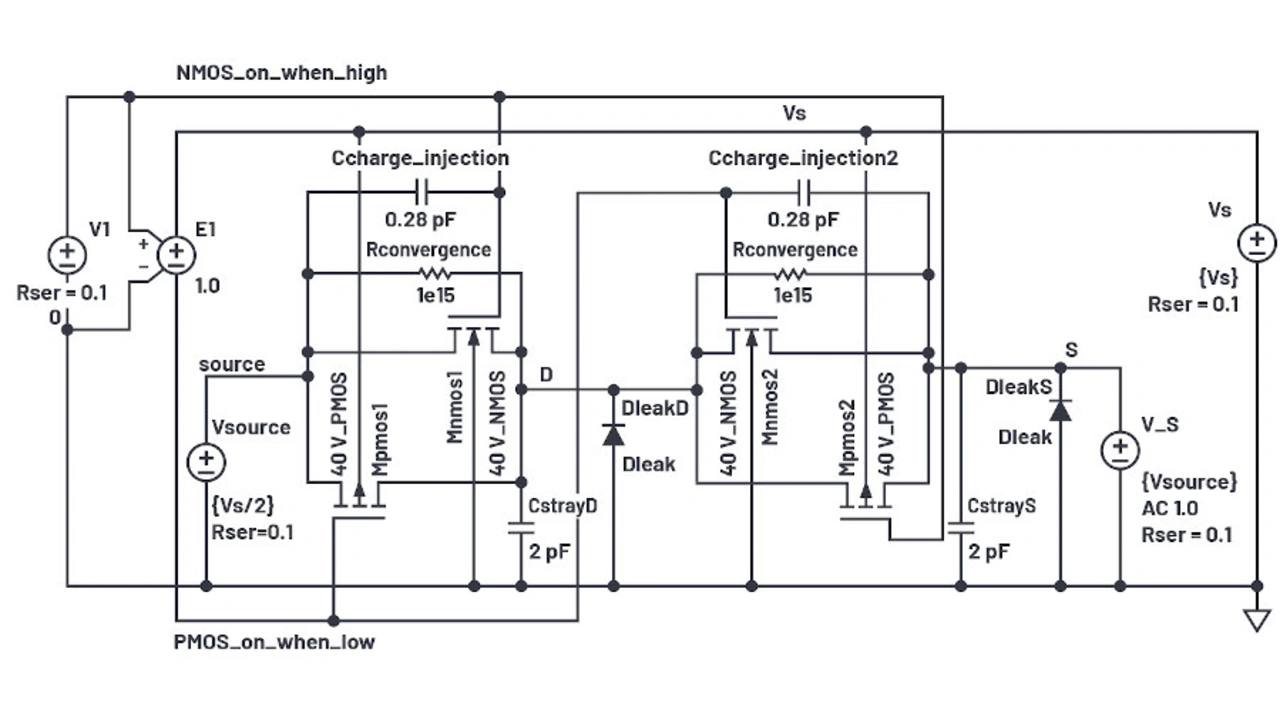
Das Modell zeigt keine Leckströme jenseits der Ströme über RCONVERGENCE und GMIN. GMIN ist ein Widerstand, den der Simulator über Verbindungen platziert, um die Konvergenz zu erleichtern. Normalerweise hat dieser einen Leitwert von 1 × 10–12, aber bei Versorgungsspannungen von 30 V kann ein Vielfaches von 30 pA erreicht werden, was für diese Aufgabe viel zu hoch ist. GMIN wird deshalb in der Zeile .options der Simulation auf 1 × 10–15 verringert und RCONVERGENCE auf 1 × 1015 erhöht.
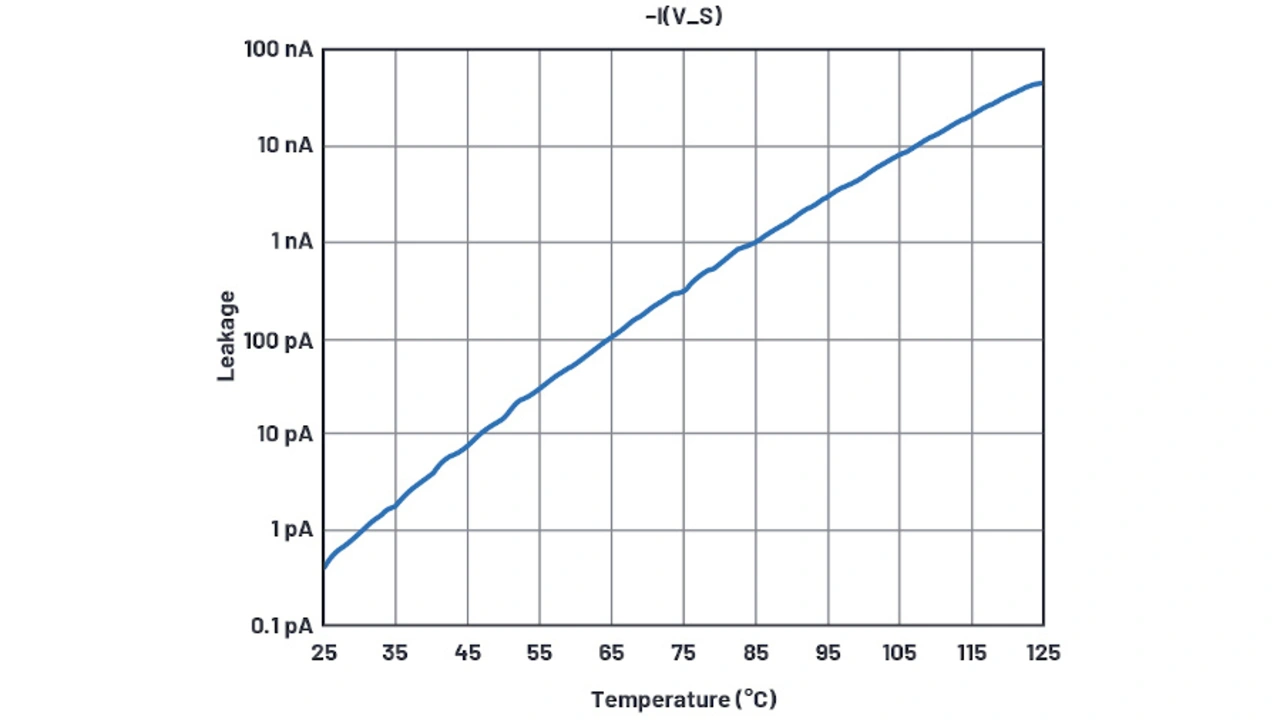
Der physikalische Ursprung dieser Leckströme sind vermutlich größtenteils die an jedem Pin angeschlossenen Schutzdioden gegen elektrostatische Entladung (ESD). Die um ESD-Dioden erweiterte Schaltung ist in Bild 16a dargestellt. Nach dem Anpassen von IS im Diodenmodell lassen sich die Leckströme über die Temperatur simulieren (Bild 17).
Logik-Schnittstelle und Gate-Treiber
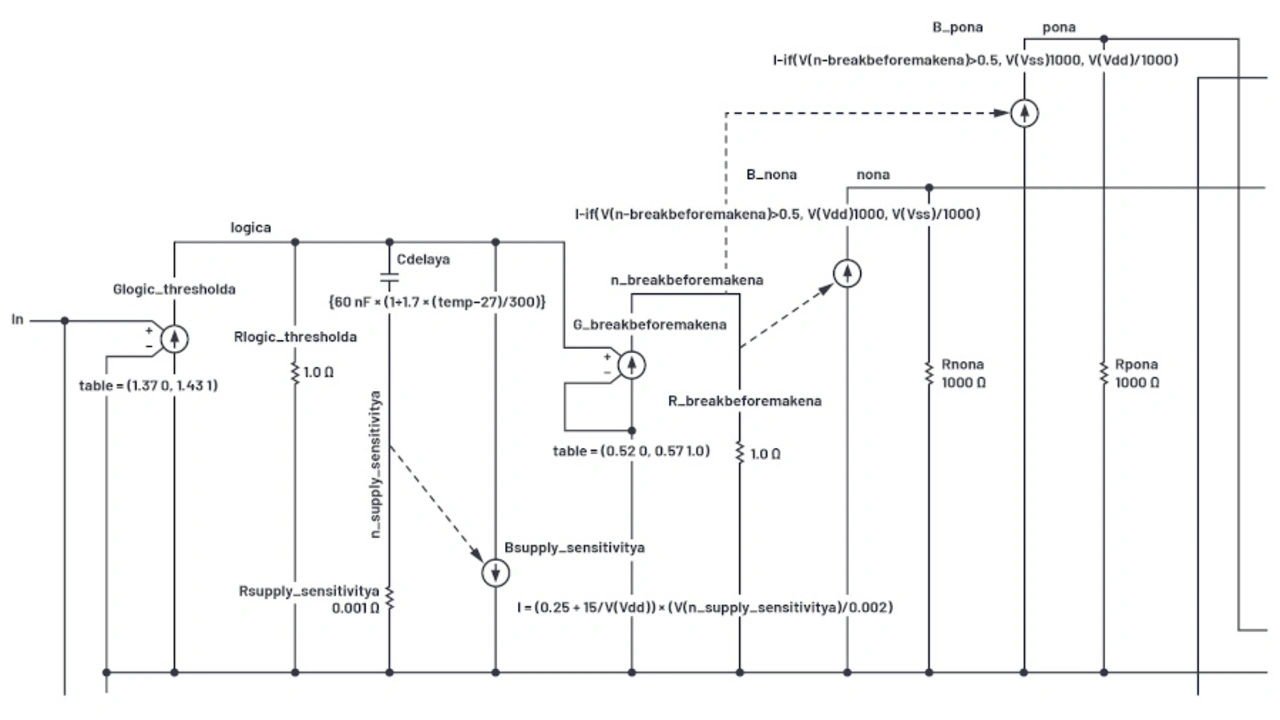
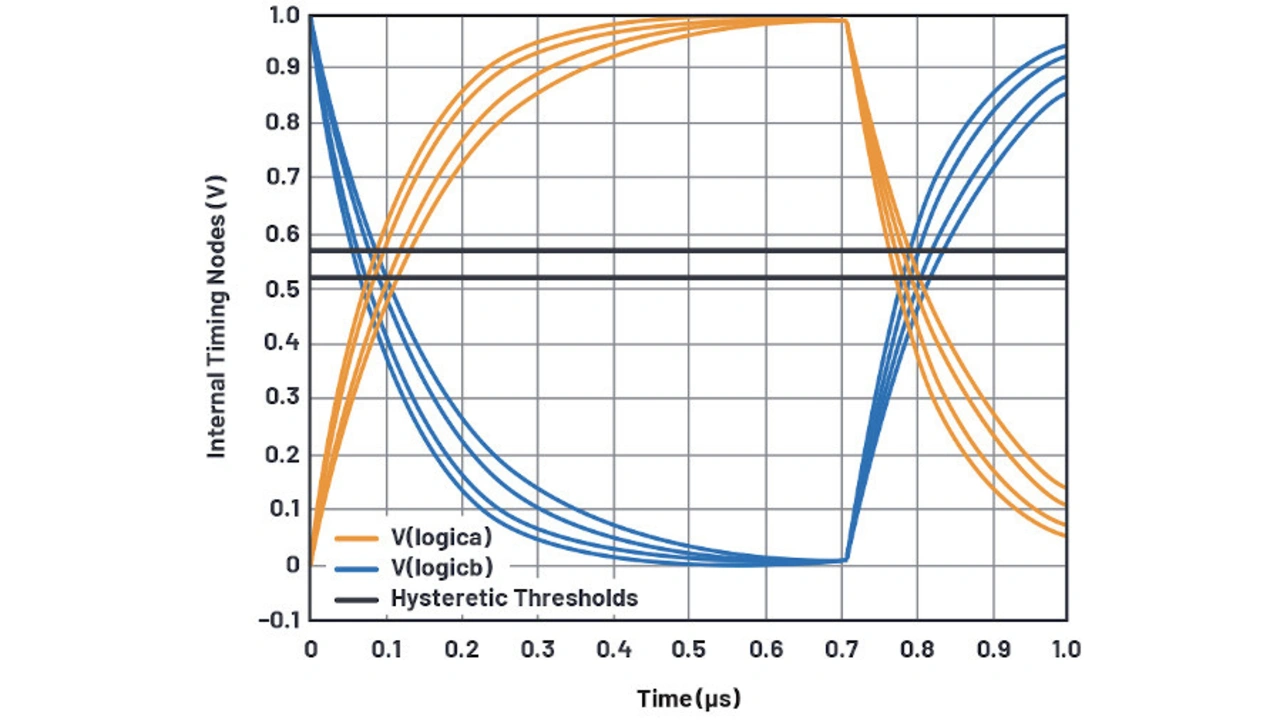
In der rein verhaltensbasierten Logik als Gate-Treiber (Bild 18) befindet sich der externe Logikeingang am In-Anschluss links. Es ist der Eingang einer idealen Transkonduktanz Glogic_thresholda, die eine stückweise lineare Übertragungsfunktion hat. Bei Logikeingängen unter 1,37 V beträgt der Ausgang am Logikknoten 0 V; bei Eingängen über 1,43 V liegt logica bei 1 V; und zwischen 1,37 V und 1,43 V bewegt sich logica linear von 0 V auf 1 V. Glogic_thresholda ignoriert also Versorgungsspannungsschwankungen, um eine Eingangsschwellenspannung von 1,4 V bereitzustellen.
Cdelaya verlangsamt kurzzeitig den Knoten logica, so dass sich einige Zeitpunkte herausgreifen lassen. Um einen Komparator zu erzeugen, wird wieder eine Transkonduktanz verwendet, hier Gbreakbeforemakena, deren Ausgang wieder von 0 V auf 1 V geht, jedoch mit einem etwas über 0,5 V verschobenen Schwellenwert. Wie in den Bildern 19a und 19b zu sehen ist, ermöglichen die verschobenen Schwellenspannungen – 0,52 V und 0,57 V anstelle von 0,5 V – ein schnelleres Abschalten bei exponentiellen Spannungsänderungen von 1 V abwärts, als der Einschaltvorgang für exponentielle Spannungsanstiege von 0 V aus.
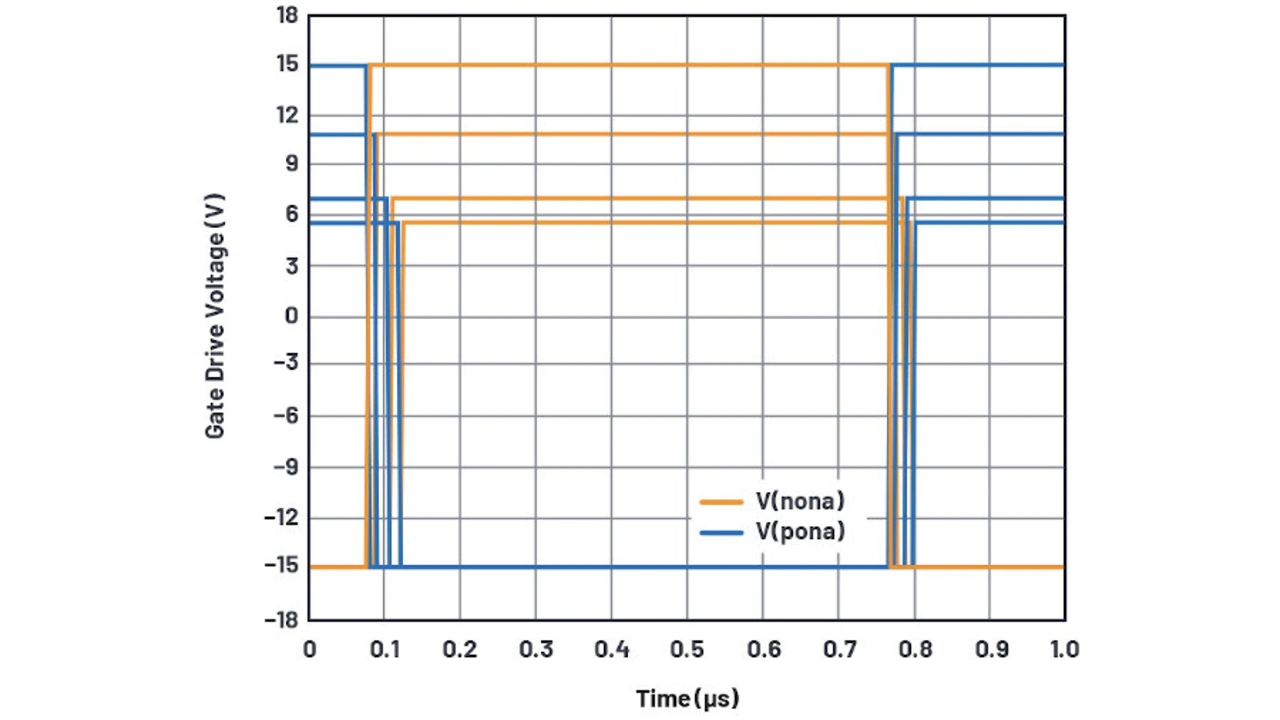
Die Gate-Treiberspannung wird von den Stromquellen mit B_non- und B_pon-Verhalten erzeugt. B_nona liefert einen Strom von VDD/1000, wenn der Knoten n_breakbeforemakena >0,5 V ist, und treibt die Spannung am Knoten nona auf VDD, belastet mit einem 1000 Ω-Widerstand.
Wenn der Knoten n_breakbeforemakena <0,5 V ist, wird der Knoten nona auf VSS geschaltet. Somit ergibt sich ein schöner Rail-to-Rail-Gate-Treiber, der mit den Versorgungsspannungen kompatibel ist und eine feste Eingangsschwelle von 1,4 V hat.
Es gibt noch eine weitere Eigenschaft, die einer Erklärung bedarf und zu beachten ist. Die Verzögerungszeiten in Bild 20 werden durch höhere Versorgungsspannungen verkürzt. Dies wird mittels B_supplysensitivitya implementiert. Damit wird ein Bruchteil des eigenen dynamischen Stroms, der in Abhängigkeit vom VDD variiert, an Cdelaya zurückgeführt. An Rsupply_sensitivitya fällt aufgrund des Cdelaya-Stroms nur sehr wenig Spannung ab, so dass sich Cdelaya im Grunde wie ein reiner Kondensator verhält. Das Einspeisen einer Kopie des Stroms von Cdelaya zurück zu Cdelaya erzeugt im Wesentlichen einen steuerbaren variablen Kondensator und die Berechnungen in Bsupply_sensitivitya erzeugt die Kurve der Verzögerung gegenüber VDD in Bild 20.
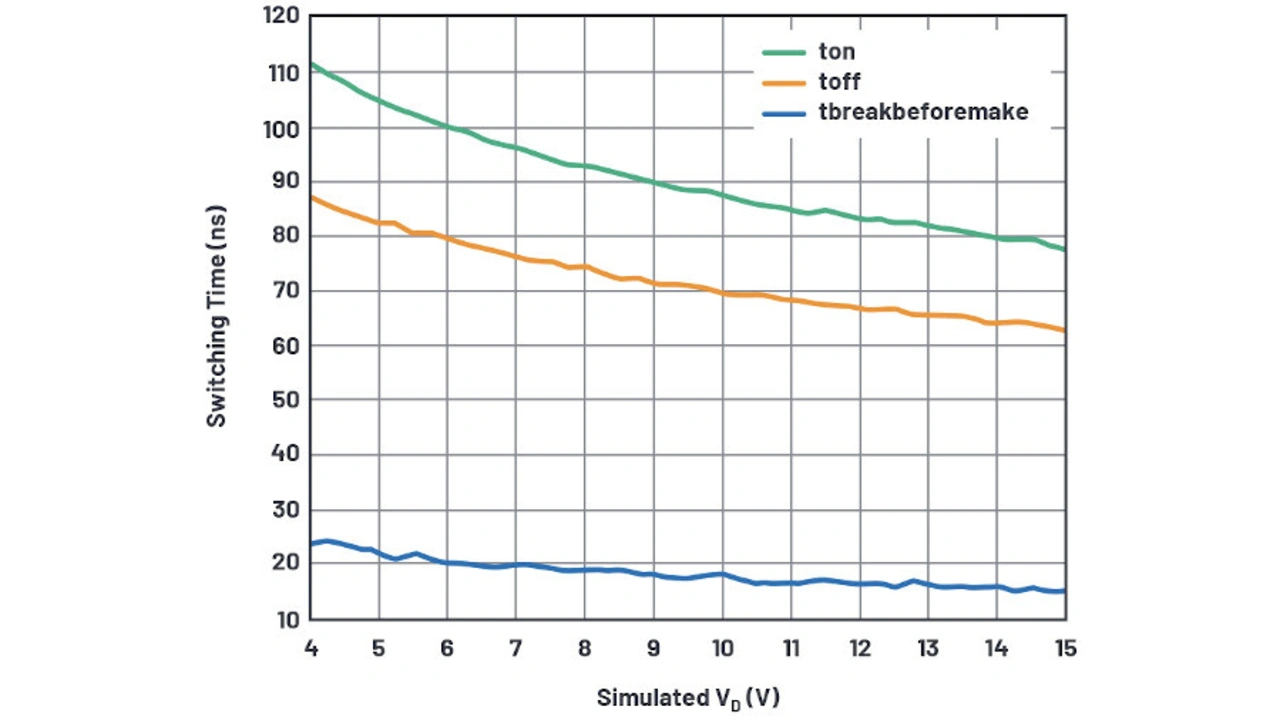
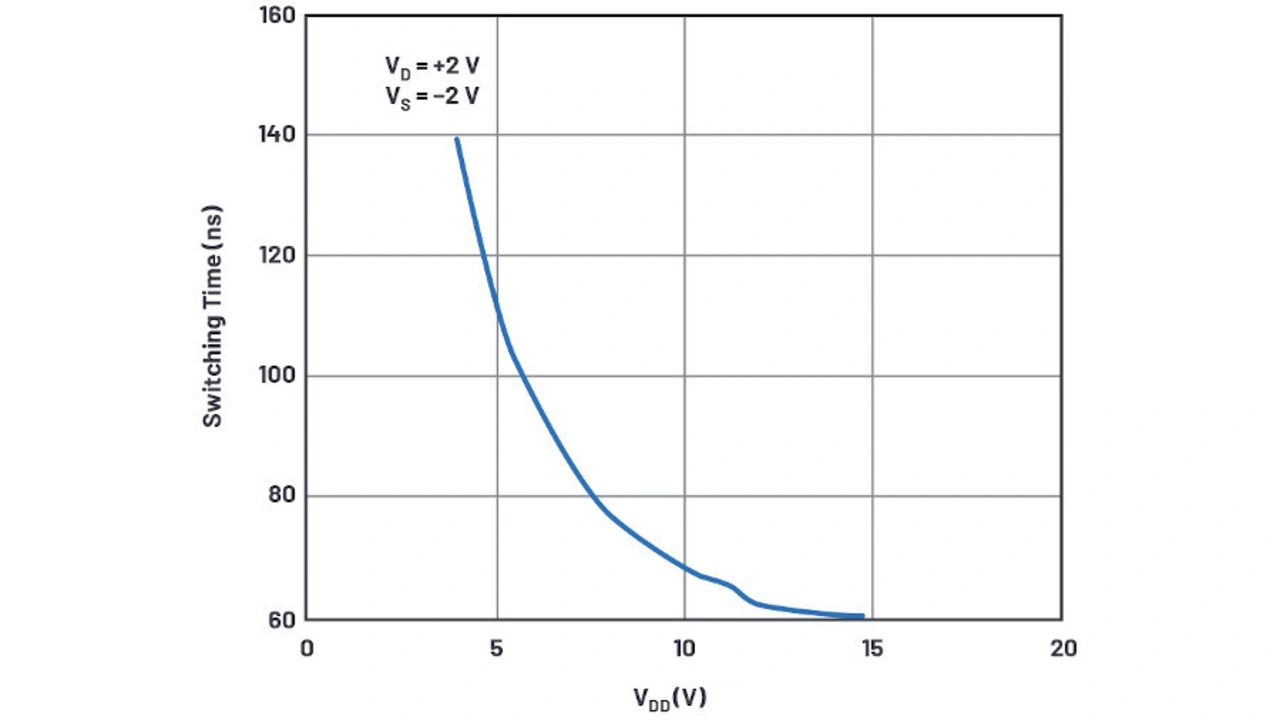
Nun emuliert unsere Schaltung die TEin-Verzögerung als 111 ns für VDD = 4 V, wogegen die Datenblattkurve 140 ns angibt. Für VDD = 15 V beträgt die simulierte Verzögerung 77 ns gegenüber einer Verzögerung von 60 ns im Datenblatt. Dies ist keine besonders gute Korrelation. An dieser Stelle bleibt es dem Leser überlassen, die Funktion Bsupply_sensitivity zu verfeinern, um das Zeitverhalten zu verbessern. Immerhin variiert die Zeit zwischen Öffnen des einen Analogschalters und Schließen des anderen Analogschalters schön zwischen 15 ns und 24 ns.
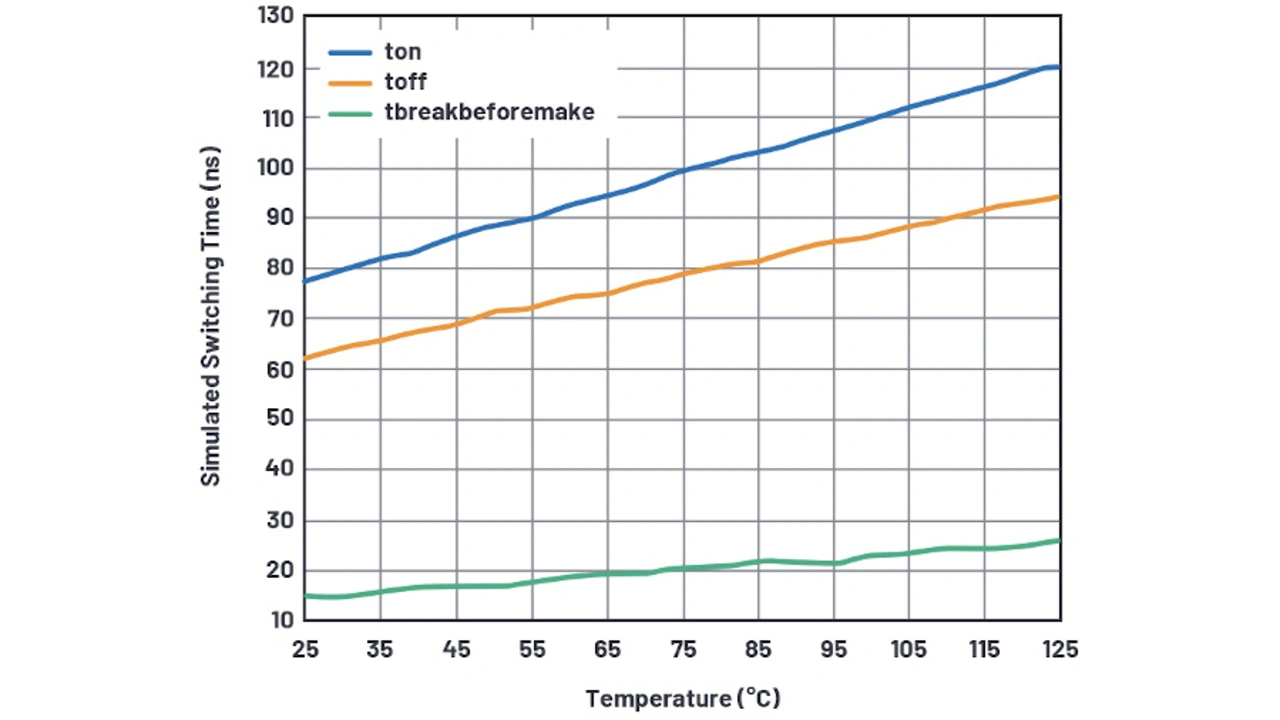
Zwar enthält das Datenblatt [2] wenig Daten bezüglich der Temperaturabhängigkeit der Verzögerung, aber es lässt sich ein Temperaturterm zu Cdelaya hinzufügen, um zumindest die Verlangsamung des Modells im heißen Zustand zu ermöglichen, wie in Bild 21 zu sehen ist.
- Das Erstellen eigener SPICE-Modelle ist nicht schwer
- Modellparameter ermitteln
- Zusammensetzen des kompletten Makromodells
- Übersicht der Bilder
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Trennverstärker
Spannungen in Antrieben isoliert erfassen
Schaltungsentwurf mit LTspice
Aufwärtswandler richtig auslegen
Welcher Schutz ist der richtige?
Teure Halbleiter vor Überspannungen/Überströmen schützen
