LTspice-Makromodelle für Analogschalter

Das Erstellen eigener SPICE-Modelle ist nicht schwer

14. Juni 2021, 6:00 Uhr | Barry Harvey

Verfügbare Simulationsmodelle für Analogschalter berücksichtigen nicht das Temperaturverhalten und sind nur für eine bestimmte Versorgungsspannungen definiert. Wer ihr Spannungs- und Temperaturverhalten simulieren will, muss selbst ein Makromodell erstellen – auf der Basis einfachster Modelle.

Beim Testen einer Schaltung mit Analogschaltern und Operationsverstärkern konnte ich viele Abweichungen von meinem Entwurf feststellen, den ich auf Papier erstellt hatte. Die Dynamik der Schaltung war anders als erwartet, und der Rauschpegel war viel größer als gefordert. Ich musste die Schaltung mit einem Simulator untersuchen, um sie vollständig zu verstehen.

Für die verwendeten Operationsverstärker gibt es gute Makromodelle, aber das Makromodel für die Analogschalter wurde nicht für allgemeine Anwendungen konzipiert. Im Kopf der Makromodelldatei des Schalters steht die Warnung, dass die modellierten Parameter nur für eine bestimmte Versorgungsspannung und Temperatur gültig sind. Nun, meine Schaltung hatte in der Tat andere Betriebsbedingungen als im Modell spezifiziert.

Das Schwierige mit Analogschaltern ist, dass sie so universell einsetzbar sind und ein Arbeitspunkt nicht ausreicht. Beim genauen Betrachten der verschiedenen Analogschalter-Makromodelle von Analog Devices und anderen IC-Herstellern, fällt auf, dass in allen Dateiköpfen angegeben ist, dass keine Versorgungsspannungs- oder Temperaturabhängigkeit modelliert wird. Dafür muss ein eigenes Makromodell erstellt werden. Die vorhandenen Standardmodelle der Halbleiterhersteller sind zwar ein guter Ausgangspunkt, aber um eine sehr leistungsfähige Analogschaltung zu entwerfen, ist möglicherweise ein neuer Modellierungsansatz für die Simulation erforderlich.

Meine Philosophie für das Modellieren der Analogschalter ist die Kombination zweier Ansätze: In den Analogschaltern werden vollständige Transistoren mit den einfachsten Bauteilmodellen verwendet, die sämtliche zu emulierenden Verhalten liefern, und für die Schnittstelle vom Steuer-Pin zu den MOS-Gattern werden die einfachsten, verhaltensmodellierten Komponenten verwendet.

Die im folgenden beschriebenen Arbeiten wurden mit dem LTspice-Simulator [1] durchgeführt; der Code würde aber auch auf anderen Simulatoren funktionieren, wenn die LTspice-Verhaltenskomponenten in SPICE-ähnliche Polynomfunktionen übersetzt werden.

Modellparameter für den Ein-Widerstand

Für die Simulation realer MOS-Bausteine wird das einfachste Modell genutzt. Zur Modellierung des Ein-Widerstands dienen die folgenden Parameter:

W/L, die Kanalbreite (W) geteilt durch die Kanallänge (L) eines MOSFETs. W/L ist die Größe oder relative Dicke des Bauteils.
U_F, die Schwellenspannung; und Gamma, das den Wert für U_F entsprechend der Sperr-Vorspannung des Bauteils modifiziert. Die Sperr-Vorspannung ist die Spannung zwischen dem Einschaltelement und dessen Substratspannung; das Substrat des Schalters ist für den PMOSFET häufig mit der positiven Versorgungsspannung und für den NMOSFET mit der negativen Versorgungsspannung verbunden.
KP, im Modell, auch als k’ oder k prime bekannt. Dieser Parameter modelliert die Stärke des Prozesses und wird mit W/L multipliziert, um MOS-Ströme zu skalieren. Für einen gegebenen Prozess hat der NMOSFET ungefähr den 2,5-fachen KP-Wert des PMOSFET.
R_D, der parasitäre Widerstand des Drain-Anschlusses des Bauteils.

Verschiedene MOS-Prozesse haben unterschiedliche intrinsische Parameter. In der Tabelle sind gängige CMOS-Prozesse, ihre Eigenschaften und wesentlichen Parameter (abgeschätzt) im Zusammenhang mit dem Ein-Widerstand zusammengestellt.

Betriebsspannung [V]	Bauteilkonstruktion	Gateoxiddicke [m]	U_F [V], n/p	Gamma [V^0,5], n/p	KP [µA/V²] n/p	L [µm]	R_D [Ω] n/p
40	Drain-Drift-Region	10^–7	0,7/–0,9	0,4/–0,57	11/5	2	~80 % von R_DS,Ein
15	Soft-Drain-Diffusion	4 × 10^–8	0,7/–0,9	0,4/–0,57	22/10	1,5	~20 % von R_DS,Ein
5	Einfach	1,4 × 10^–8	0,7/–0,9	0,4/–0,57	80/28	0,5	~0

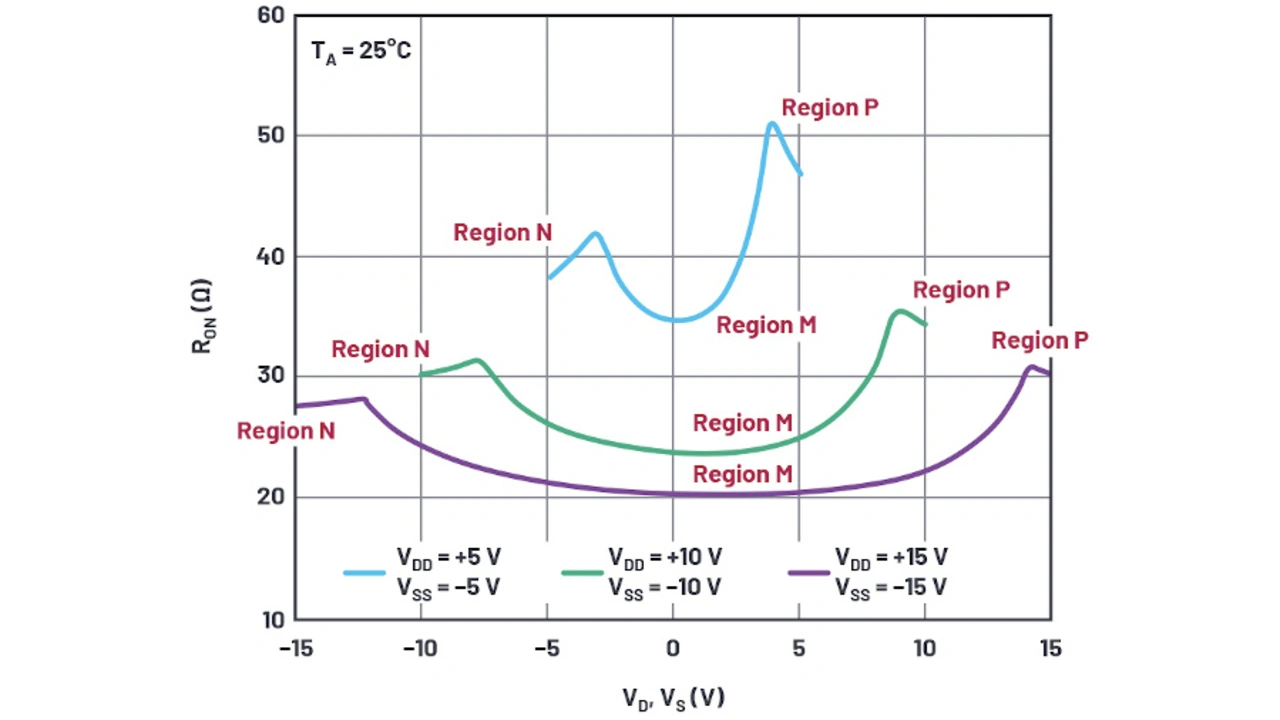
In Bild 1 ist der Verlauf des Ein-Widerstandes (R_Ein) für den ADG333A [2] in Abhängigkeit von der Versorgungsspannung dargestellt. Darin ist als allgemeiner Trend für diesen und alle anderen Analogschalter zu erkennen, dass höhere Versorgungsspannungen den Ein-Widerstand verringern. Je höher die an die MOS-Gates des Analogschalters angelegte Spannung ist, desto geringer wird der Ein-Widerstand. Zu beobachten ist auch eine deutliche Veränderung des Widerstands über den analogen Pegel. In den N-Regionen ist der NMOSFET eines Analogschalters vollständig eingeschaltet. Wenn die Analogspannung über die negative Linie ansteigt, schaltet sich der PMOSFET ein und trägt zur Verringerung des Gesamt-Ein-Widerstands bei. Der Wendepunkt in der N-Region liegt ungefähr um die Schwellenspannung des PMOSFET über der negativen Versorgungsspannung.

In gleicher Weise ist in den P-Regionen der PMOSFET des Analogschalters vollständig eingeschaltet, und der NMOSFET beginnt ungefähr ab der Schwellenspannung des NMOSFET unterhalb der positiven Versorgungsspannung den PMOSFET zu unterstützen.

Die M-Regionen (Bild 1) befinden sich in der Mitte der N- und P-Regionen, in welcher der NMOS- und der PMOSFET parallel arbeiten, aber je nach dem analogen Signalpegel zwischen den Versorgungen einen unterschiedlichen Ein-Widerstand aufweisen.

Um mit der Kurvenanpassung zu beginnen, ist zunächst die Größe eines jeden einzelnen FETs zu schätzen. Die Kleinspannungskurve liefert die beste Kurvenanpassung für R_DS,Ein des FETs. In der Region N, mit einem Analogsignal in der Nähe der negativen Versorgungsspannung, ist der PMOSFET ausgeschaltet und R_Ein des Analogschalters ist gleich dem R_Ein des NMOSFETs. Für die Berechnung dient die folgende Gleichung:

$R subscript D S comma E i n end subscript equals fraction numerator I over denominator K P begin display style W over L end style open parentheses U subscript G S end subscript minus U subscript F close parentheses end fraction$

Ausgehend von den typischen 40-V-NMOS-Prozesswert lässt sich in der Kurve in Bild 1 ein R_DS,Ein = 38 Ω ablesen. Mit den in der Tabelle angegebenen Prozessgrößen errechnet sich die Kanalbreite des NMOSFETs:

$W subscript N M O S end subscript equals fraction numerator 2 space mu A over denominator 38 space capital omega space cross times 11 cross times 10 to the power of negative 6 end exponent begin display style fraction numerator mu A over denominator V squared end fraction end style cross times open parentheses 10 space V space minus space 0 comma 7 space V close parentheses space end fraction equals 514 space mu m$

Der PMOSFET, mit einem Ein-Widerstand von 47 Ω aus der Kurve in Bild 1, hätte damit eine Kanalbreite von 936 µm.

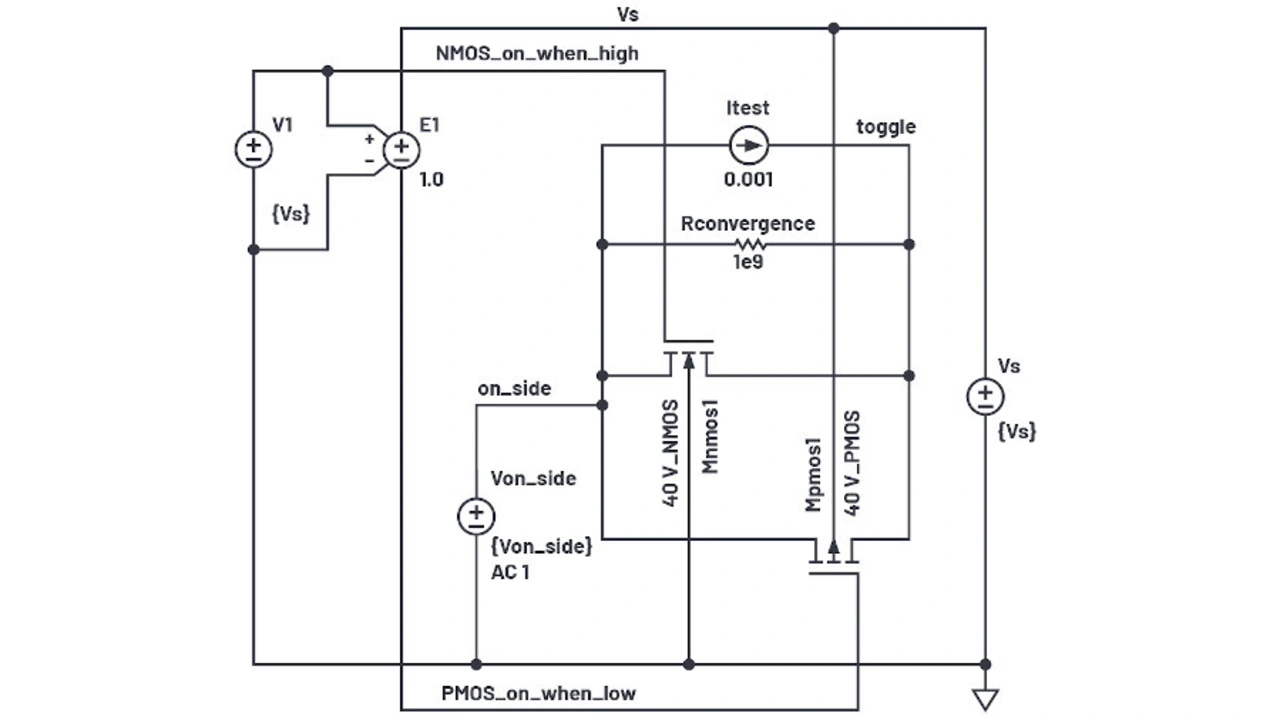
Ausgangspunkt für das neue Modell ist die in Bild 2 gezeigte LTspice-Testschaltung. Zu beachten ist, dass die Parameter R_DN und R_DP, die parasitären Drain-Widerstände, einen eher moderaten Wert haben. Wird zum Beispiel ein Wert von 1 µ genommen, führt dies zu einer langsamen Konvergenz der Simulation. Ein R_DN-Wert von 1 dagegen ermöglicht eine angemessene Simulationsgeschwindigkeit. Das Hinzufügen eines Widerstandes R_Konvergenz hat das Simulationsrauschen und die Simulationsgeschwindigkeit verbessert, indem dem Umschaltknoten eine konvergenzfähige Leitfähigkeit verliehen wurde. Für die Messung des Ein-Widerstands wurde eine potentialfreie Stromquelle getestet.

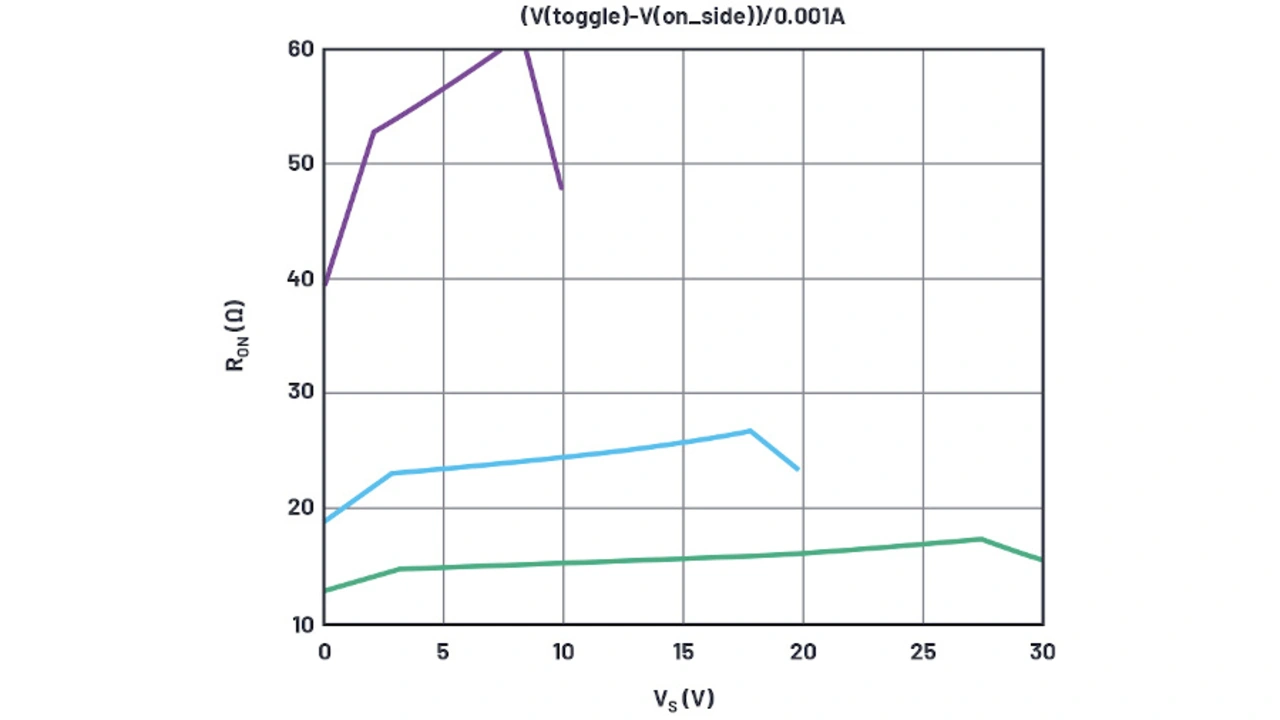
In Bild 3 sind die per Simulation ermittelten Ein-Widerstände der Analogschalter-Testschaltung aus Bild 2 für verschiedene Versorgungsspannungen dargestellt. Das Diagramm zeigt, dass die gewählte Testschaltung sich ganz gut eignet. Der Knick am unteren Ende des Spannungsbereichs für eine Spannung am Anschluss S von 30 V liegt bei 3,6 V in der Simulation und bei 2,7 V im Datenblatt. Die Abweichung legt nahe, den PMOSFET-U_F-Wert zu reduzieren, allerdings ist 0,9 V bereits ein realistisches Minimum. Besser ist es daher, den Gamma-Wert des PMOSFET anzupassen, der ohnehin nur ein Schätzwert war.

Der Knick in der Nähe der maximalen Versorgungsspannung liegt 2,5 V unterhalb der 30-V-Versorgungsspannung, laut Datenblatt sollte er dagegen bei ~1 V Differenz liegen. Werden hier verschiedene Gamma-Werte in der Simulation genutzt, so führt das zu einer Überhöhung der Knickspannung von der Versorgungsspannung. Deshalb empfiehlt es sich daher einfach die NMOSFET-U_F auf 1 V und dessen Gamma auf null setzen. Ein Gamma von Null ist zwar nicht zu erwarten, aber es geht ja nur darum, sich der Kurve anzupassen.

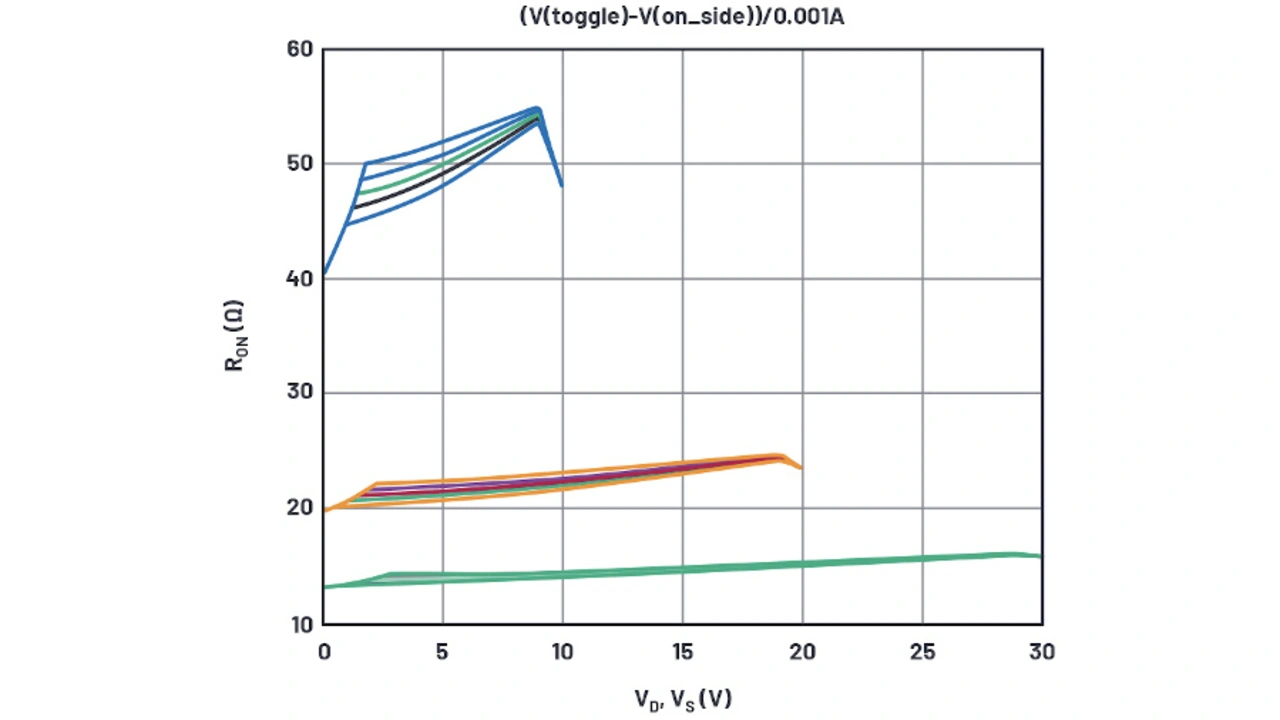
Bild 4 zeigt die Simulationsergebnisse aus diesen Werten, wobei der Gamma-Wert des PMOSFET für verschiedene Versorgungsspannungen stufenweise erhöht wurde. Für die weiteren Betrachtungen werden die 30-V-Kurven gewählt, bei ihnen ist der Gamma-Effekt maximal, im Vergleich zu den Kurven mit den niedrigeren Versorgungsspannungen. Aus den abgestuften Kurven wird ein PMOS-Gamma-Wert von 0,4 gewählt.

Zwar repräsentieren die 10 V-Kurven in Bild 4 die Datenblattkurve an den Extrema der Versorgungsspannung, die Simulation ergibt jedoch einen zu niedrigen R_Ein für die 20-V- und 30-V-Kurven. Die Ein-Widerstände entsprechen R_DS,Ein(NMOS) + R_D(NMOS) im Bereich nahe der positiven Versorgungsspannung und R_DS,Ein(PMOS) + R_D(PMOS) im Bereich nahe der positiven Versorgungsspannung. Bei hohen Versorgungsspannungen ist der Parameter R_D signifikanter als W/L, wogegen bei niedrigen Versorgungsspannungen W/L dominiert. Hier muss mit zwei Variablen jongliert werden, was zu mühsam ist. Es ist festzustellen, dass sich der R_Ein-Wert mit der Versorgungsspannung ändert, weil der NMOSFET variabel angereichert wird, der R_D-Wert sich jedoch nicht mit der Versorgungsspannung ändert – bei Drains mit Drift-Regionen tut er dies wahrscheinlich doch, aber das Modell soll hier einfach gehalten werden.

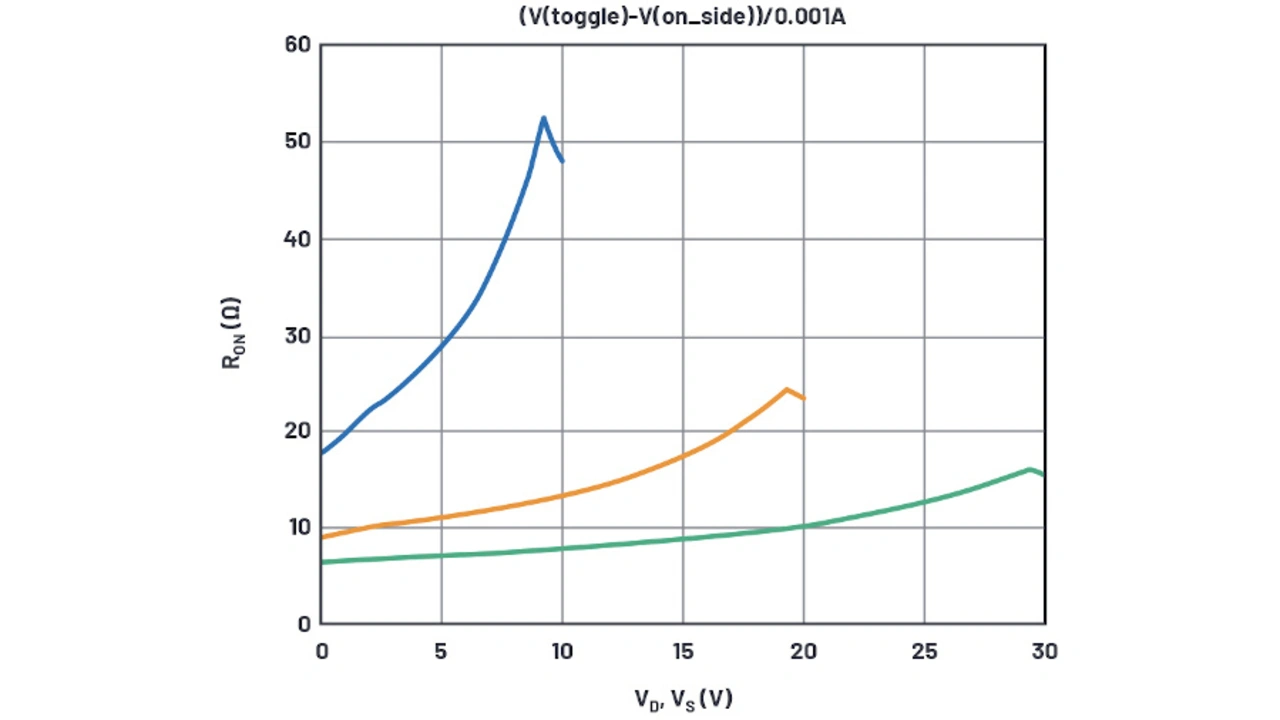
Wird der Unterschied für R_Ein im Datenblatt zwischen den Versorgungsspannungen 10 V und 30 V betrachtet (11,4 Ω), so kann dies mit den obigen Kurven verglichen werden, wobei ausschließlich nach der Breite (W_N) des NMOSFET im Analogschalter abgestuft wird. Nach ein paar Iterationen von W_N in den Simulationen ist klar, dass eine Breite W_N = 1170 µm benötigt wird, um das erforderlichen ΔR_Ein zu erhalten, also weitaus mehr als die anfängliche Schätzung. Bild 5 zeigt die mit dieser Breite erzielten Ergebnisse.

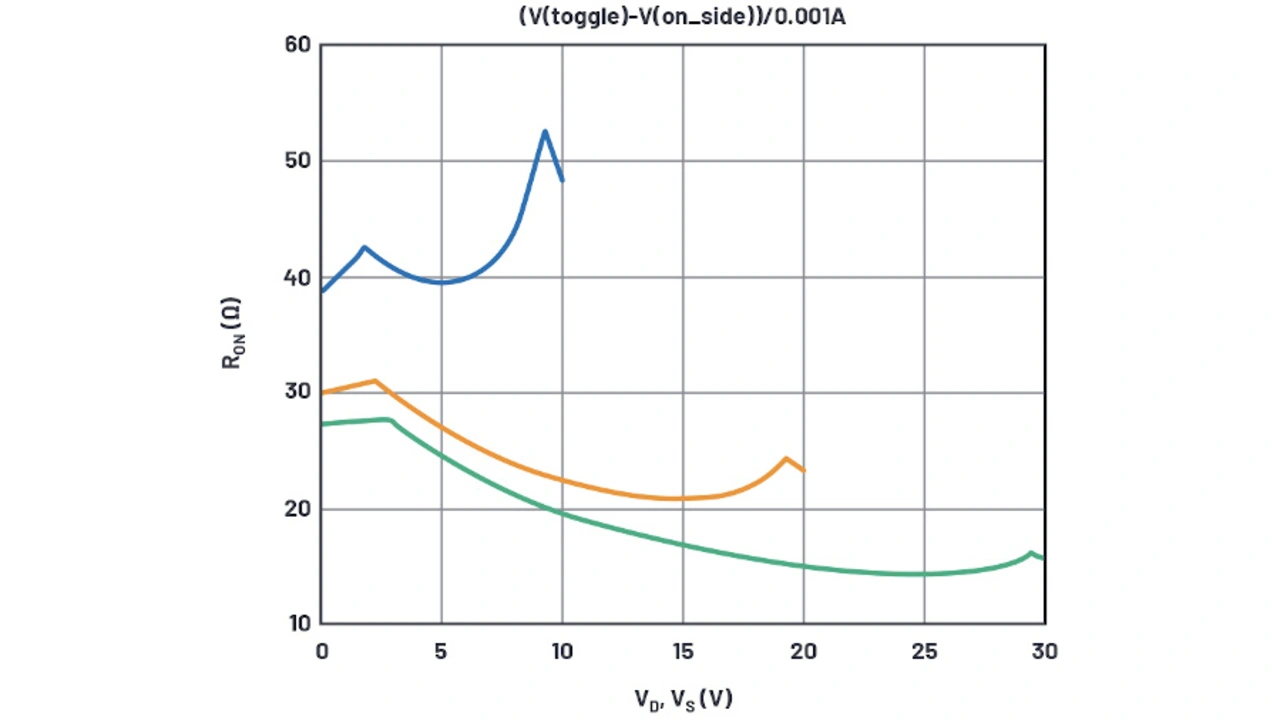
Obwohl der R_Ein des NMOSFETs die richtige Empfindlichkeit gegenüber der Versorgungsspannung aufweist, haben die Kurven bei null Volt einen zu niedrigen Wert. Deshalb muss der festgelegte Wert für R_DN erhöht werden. Nach Erhöhung und Iteration von R_DN ergibt sich ein bester Wert von R_DN = 22 Ω. Die resultierenden Kurven sind in Bild 6 dargestellt.

Als Nächstes wird mit der gleichen Methode die Kanalbreite des PMOSFETs (W_P) im Analogschalter bestimmt, um R_Ein bei maximaler Spannung zu simulieren. Auch hier ergibt sich mit W_P = 1700 µm ein Wert, der ein ganzes Stück über der anfänglich vermuteten Breite liegt. Mit einem ebenfalls auf 22 Ω festgelegten R_DP ergibt sich die endgültige R_Ein-Kurve (Bild 7).

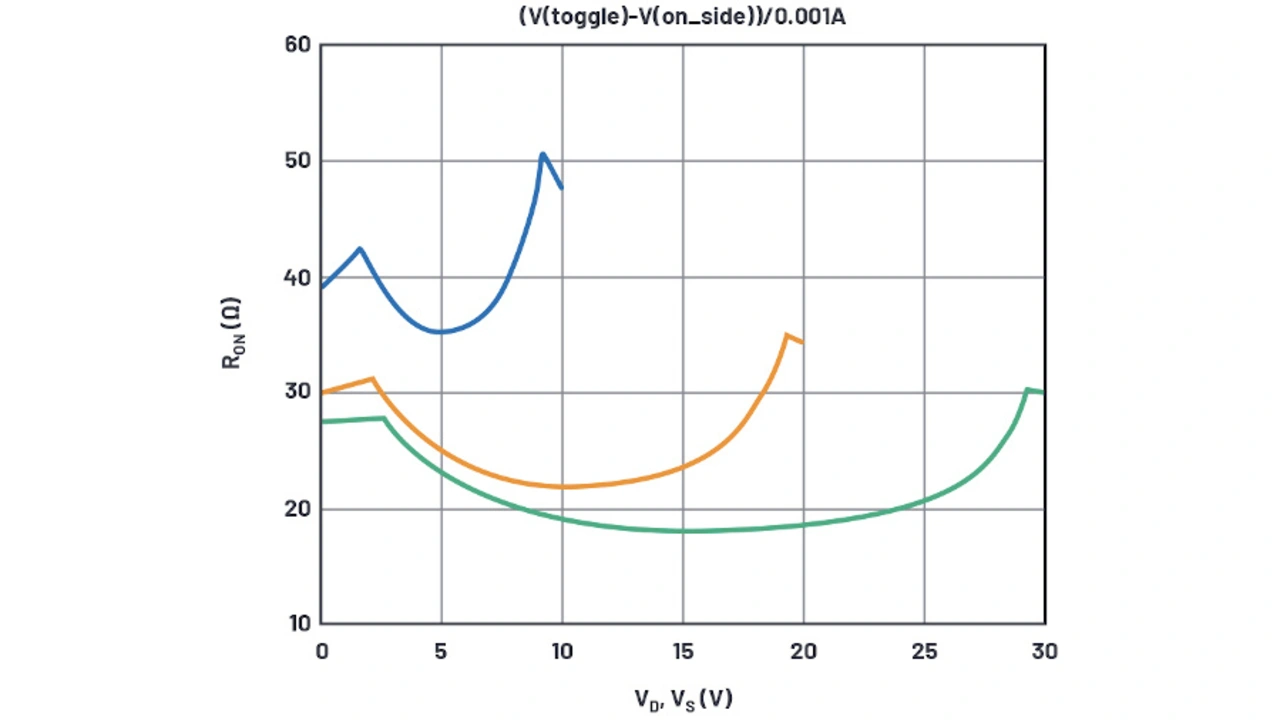
Sie zeigt eine ziemlich gute Übereinstimmung mit Bild 1; es gibt nur einige wenige Merkmale, die sich vom Datenblatt unterscheiden. Zum einen sind die Wendepunkte in der Datenblattkurve glatt, wogegen sie in der Simulation spitz sind. Dies liegt wahrscheinlich daran, dass das verwendete einfache MOS-Modell keine Unterschwelleneffekte unterstützt und das simulierte Bauelement sich bei U_F wirklich abschaltet. Reale Bauelemente sind bei U_F aber nicht ausgeschaltet, sondern verringern den Strom allmählich unterhalb dieser Spannung.

Ein weiterer Fehler ist in der 30-V-Kurve am deutlichsten zu erkennen. Der R_Ein ist im mittleren Bereich gegenüber dem Datenblatt um 15 % niedriger. Möglicherweise ist dies auf die ebenfalls nicht modellierten JFET-Effekte innerhalb der Drain-Drift-Region zurückzuführen.

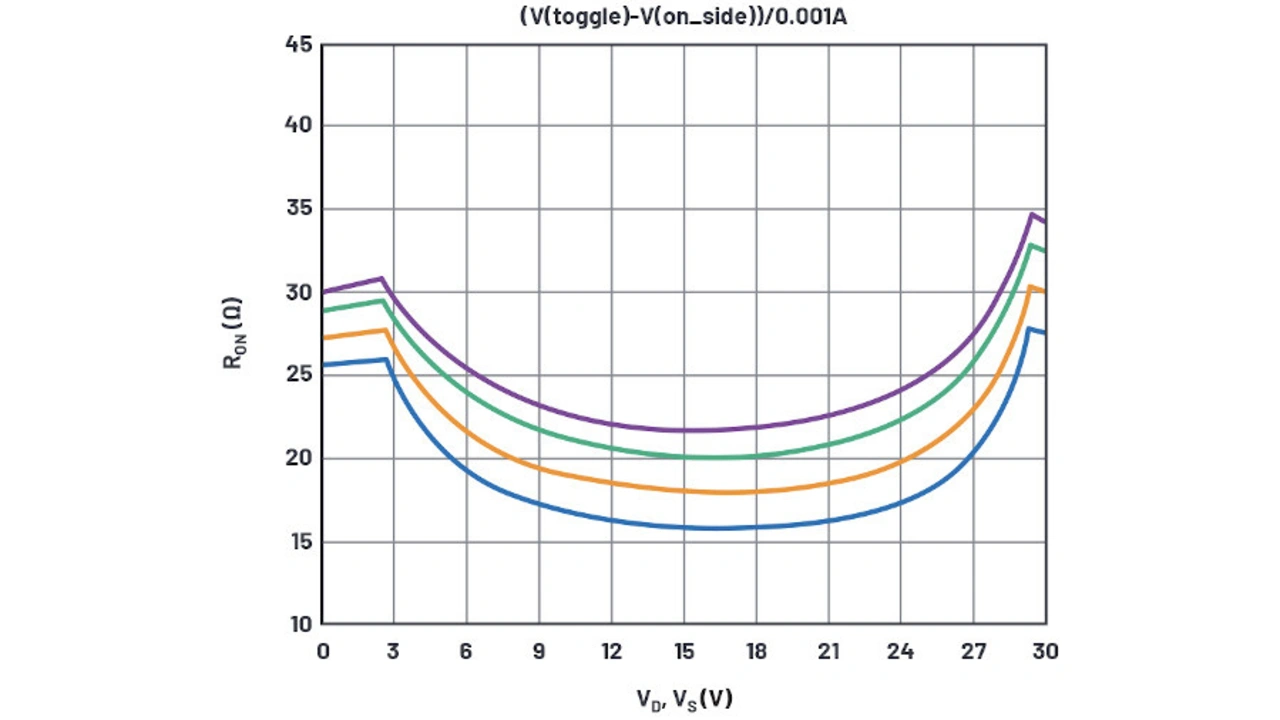
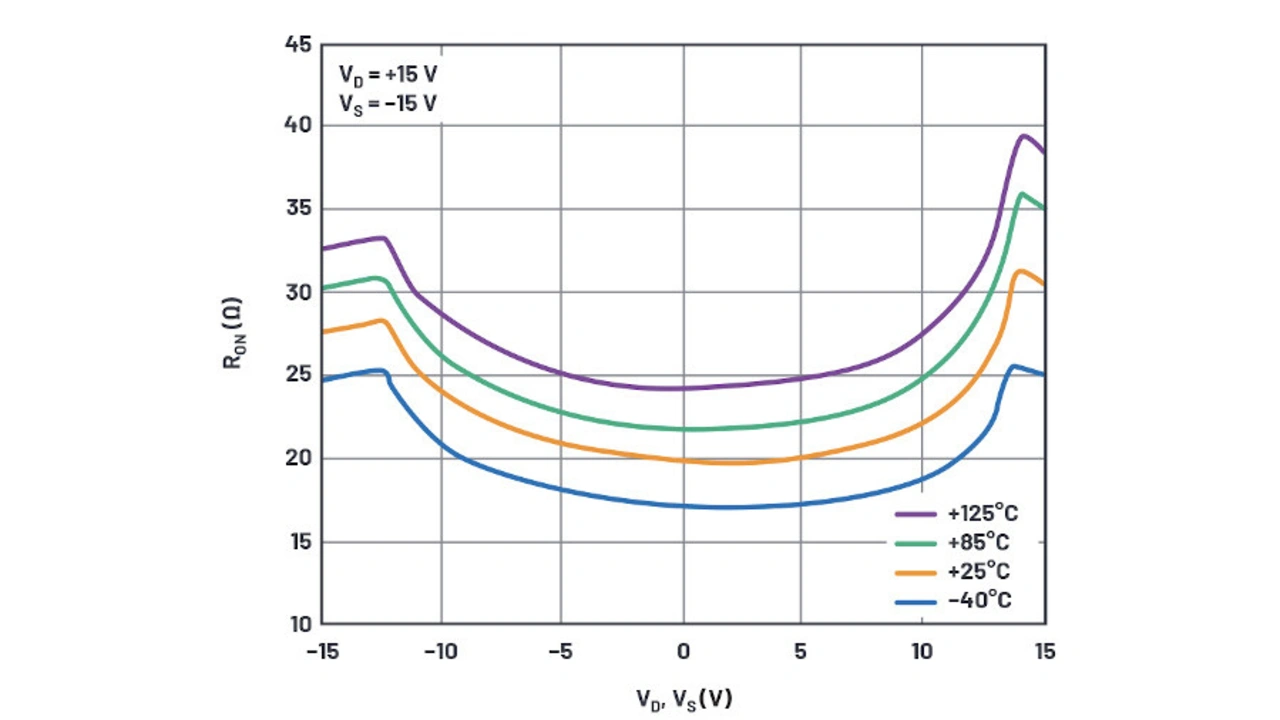
Was die Temperatur betrifft, so gibt es eine gewisse, aber nicht allzu starke Übereinstimmung, wie in den Bildern 8a und 8b zu sehen ist. Die Simulation (Bild 8a) zeigt eine Temperaturabhängigkeit, die allerdings nicht so stark ist wie die in den Datenblattkurven (Bild 8b). Im Simulationsmodell haben die R_D-Terme keine Temperaturkoeffizienten. Die parasitären Drain-Widerstände (R_DN und R_DP) könnten durch externe Widerstände mit korrekten Temperaturkoeffizienten modelliert werden, um das Modell aber möglichst einfach zu halten, wird hier jedoch darauf verzichtet.