Startseite > Kommunikation > Wireless > Werkzeug für 3D-Smith-Diagramme

S-Parameter darstellen und auswerten

Werkzeug für 3D-Smith-Diagramme

3. Januar 2019, 11:23 Uhr | Von Andrei A. Muller, Alin Moldoveanu, Victor Asavei und Cristian Fleischer

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 2

Kasten: Die Riemannsche Zahlenkugel

Die riemannsche Zahlenkugel ist benannt nach dem Mathematiker Georg Friedrich Bernhard Riemann und bietet eine Alternative, um komplexe Zahlen darzustellen.

Eine Kugel vom Durchmesser 1 wird auf den Ursprung der gaußschen Zahlenebene gelegt. Somit liegt der »Südpol« (S) der Kugel im Ursprung. Alle Punkte der gaußschen Ebene werden nun mit Geraden mit dem »Nordpol« (N) der Kugel verbunden.

Jedem Punkt der Ebene wird durch diese »stereographisch« genannte Projektion eindeutig ein Schnittpunkt der Geraden auf der Kugeloberfläche zugeordnet, der zur Darstellung der entsprechenden komplexen Zahl dienen kann:

Die Gerade des Ursprungs schneidet die Kugeloberfläche im »Südpol«,
das Innere des Einheitskreises wird auf der »südlichen« Halbkugel abgebildet,
der Einheitskreis wird auf den »Äquator« übertragen und
das Äußere des Einheitskreises wird auf der »nördlichen« Halbkugel abgebildet.

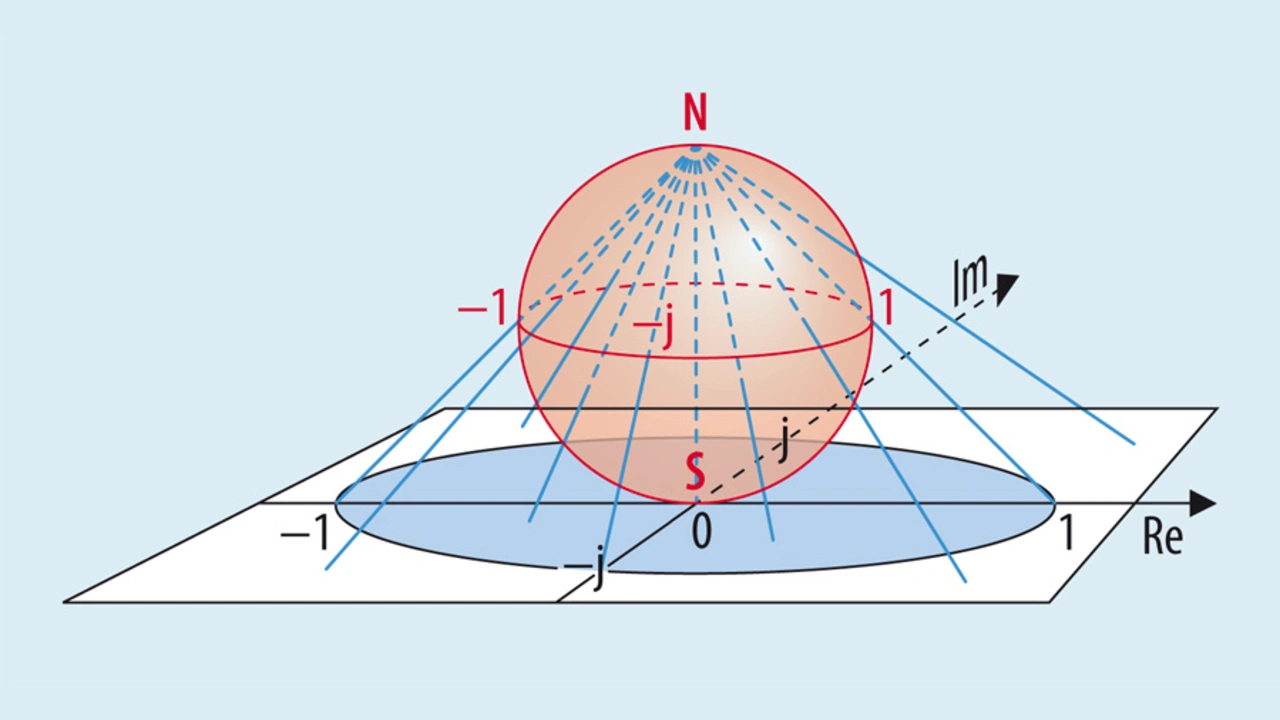
Das Interessante an dieser Darstellung ist, dass der »Nordpol« alle unendlich fernen Punkte der Ebene vereint. Damit wird zum Ausdruck gebracht, dass vom Standpunkt der komplexen Zahlen nur eine »Zahl« ∞ existiert und in deren Umgebung genauso argumentiert werden kann, wie für jede andere komplexe Zahl.

Quelle:

[8] Hefft, K.: Mathematischer Vorkurs zum Studium der Physik. Institut für Theoretische Physik, Universität Heidelberg, 17.4.2001, www.thphys.uni-heidelberg.de/~hefft/vk2/