Der Standard EMVA 1288

Lineares Kameramodell

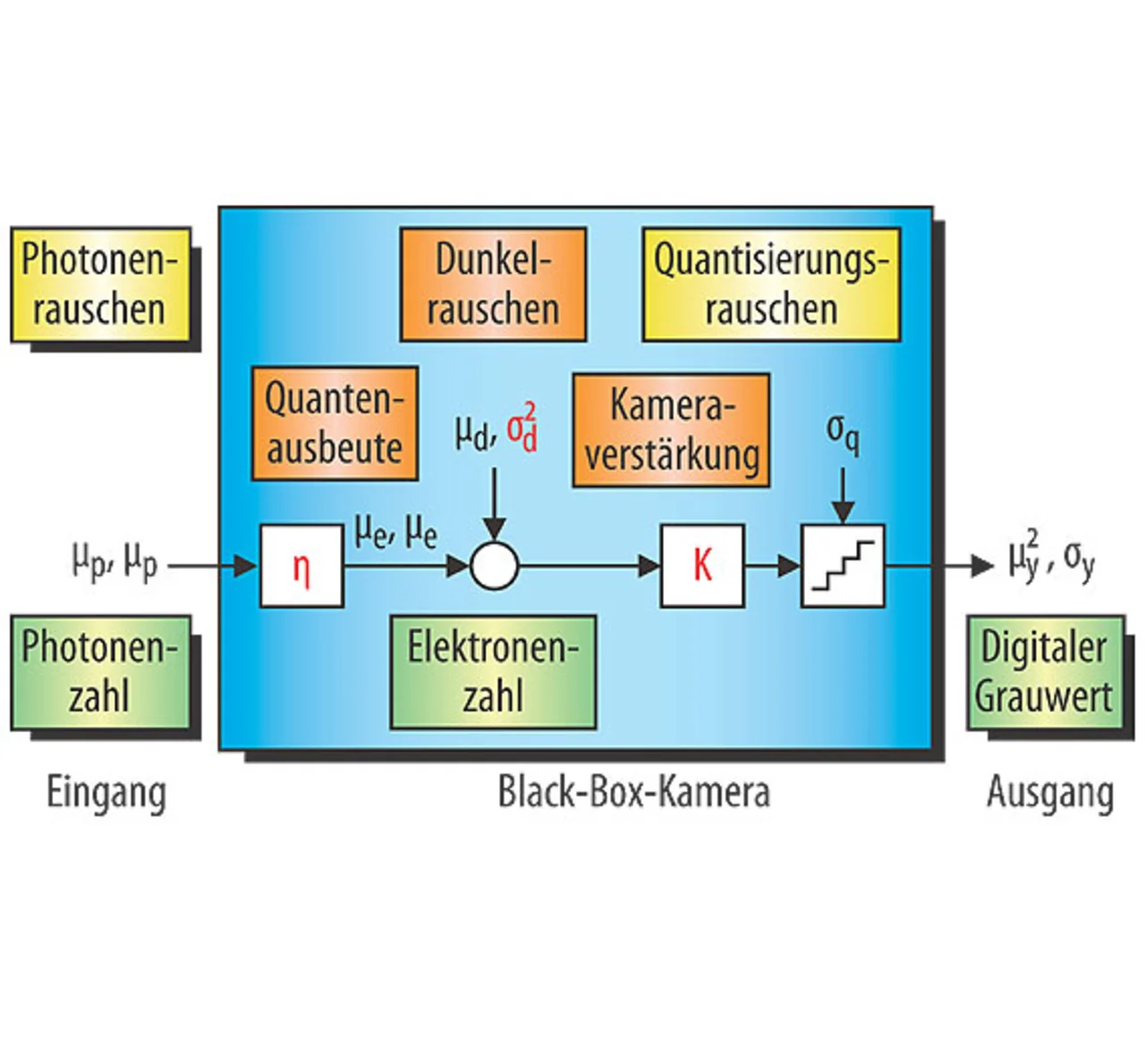
Das lineare Kameramodell beschreibt den elementaren Zusammenhang zwischen der Bestrahlungsstärke E in Anzahl Photonen pro Pixel auf der Sensorebene und dem digitalen Signal der Kamera (Grauwert y in Einheiten von digital numbers oder DN) (Bild 1). Es beinhaltet nur drei Parameter, die Quantenausbeute η, das Dunkelrauschen σd und die Kameraverstärkung K. Während der Belichtungszeit treffen im Mittel μp Photonen auf ein Sensorelement. Davon wird, abhängig von der Wellenlänge λ des einfallenden Lichtes, der Bruchteil

die Quantenausbeute η, absorbiert und in μe elektrische Ladungsträger (Elektronen) konvertiert. Zu den photoneninduzierten Ladungsträgern kommt noch das über die Belichtungszeit integrierte Dunkelsignal μd (thermisch induzierte Ladungsträger bzw. Leckströme). Dieses Signal wird verstärkt und am Ende durch einen Analog-Digital-Wandler quantisiert zu einem digitalen Grauwert

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

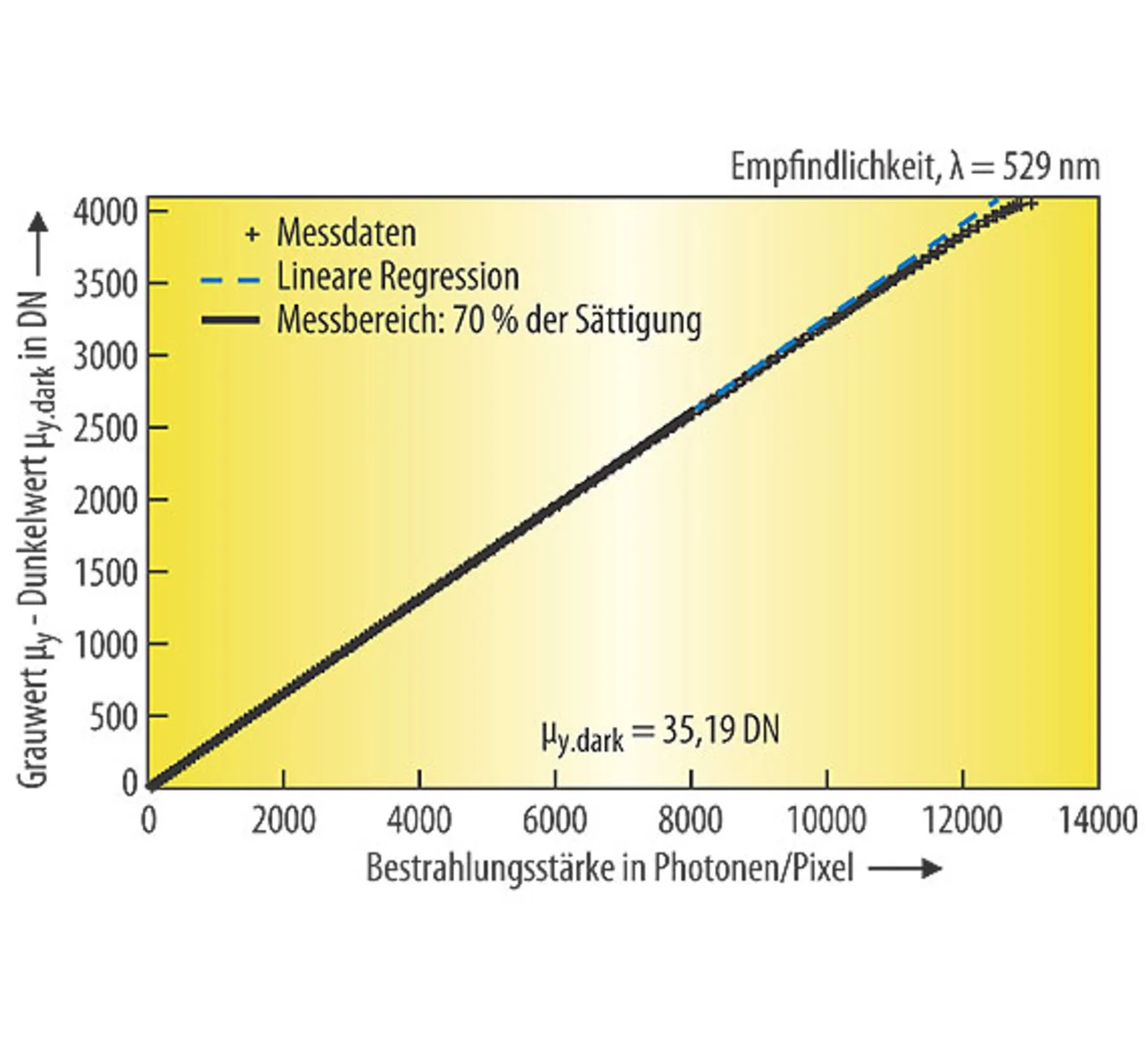
mit einem Dunkelwert μ_d (Einheit e-) bzw. μ_y.dark (Einheit DN). Die Konstante K ist der absolute Verstärkungsfaktor der Kamera und hat die einfache dimensionslose Einheit Anzahl Elektronen pro digitalem Wert (e-/DN).

Die Beziehung in Gleichung (2) kann nicht direkt bestimmt werden, da die Anzahl der Ladungsträger μ_e nicht bekannt ist. Gemessen werden kann nur der Zusammenhang zwischen der Photonenzahl/Pixel μ_p und dem mittleren Bildsignal μ_y, indem Gleichung (1) in Gleichung (2) eingesetzt wird:

Die über die Belichtungszeit texp integrierte Photonenzahl μp ergibt sich bei bekannter Pixelfläche und Wellenlänge aus der mit einer kalibrierten Photodiode bestimmte Bestrahlungsstärke E zu

Nach Gleichung (3) ist die Kamera-kennlinie linear. Der Achsenabschnitt ist das Dunkelsignal μy.dark und die Steigung das Produkt aus Verstärkungsfaktor K und der Quantenausbeute η.

Von den drei Parametern des linearen Kameramodells in Bild 1 kann daher keiner eindeutig bestimmt werden. Das ergibt sich erst aus einer Analyse des Rauschens. Das lineare Kameramodell enthält drei Rauschquellen: Das unvermeidliche Photonenrauschen (shot noise), d.h. die statistischen Fluktuationen des Photonstroms. Es ist Poisson-verteilt und die Varianz ist gleich dem Mittelwert:

Die gleiche Aussage gilt für die Varianz der über die Belichtungszeit akkumulierten Elektronen [2]:

Wegen der linearen Kamerakennlinie können alle Rauschquellen, die aus dem Transport oder der Verstärkung der Ladungsträger resultieren, in einer einzigen Rauschquelle, dem Dunkelrauschen mit einer Varianz zusammengefasst werden. Alle diese Rauschquellen werden mit dem Verstärkungsfaktor K verstärkt. Lediglich eine weitere signifikante Rauschquelle tritt nach der Verstärkung auf, das Quantisierungsrauschen. Dieses ist ein Pseudorauschen. Wenn die Quantisierungsintervalle klein genug sind, kann es als uniform betrachtet werden mit einer Varianz

Nach dem Fehlerfortpflanzungsgesetz addieren sich dann die Varianzen verschiedener Rauschquellen linear (solange die Quantisierungsstufen nicht zu grob sind, siehe [1, Appendix B4 und 3], so dass sich unter Zuhilfenahme von (2) und (3) ein Gesamtrauschen von

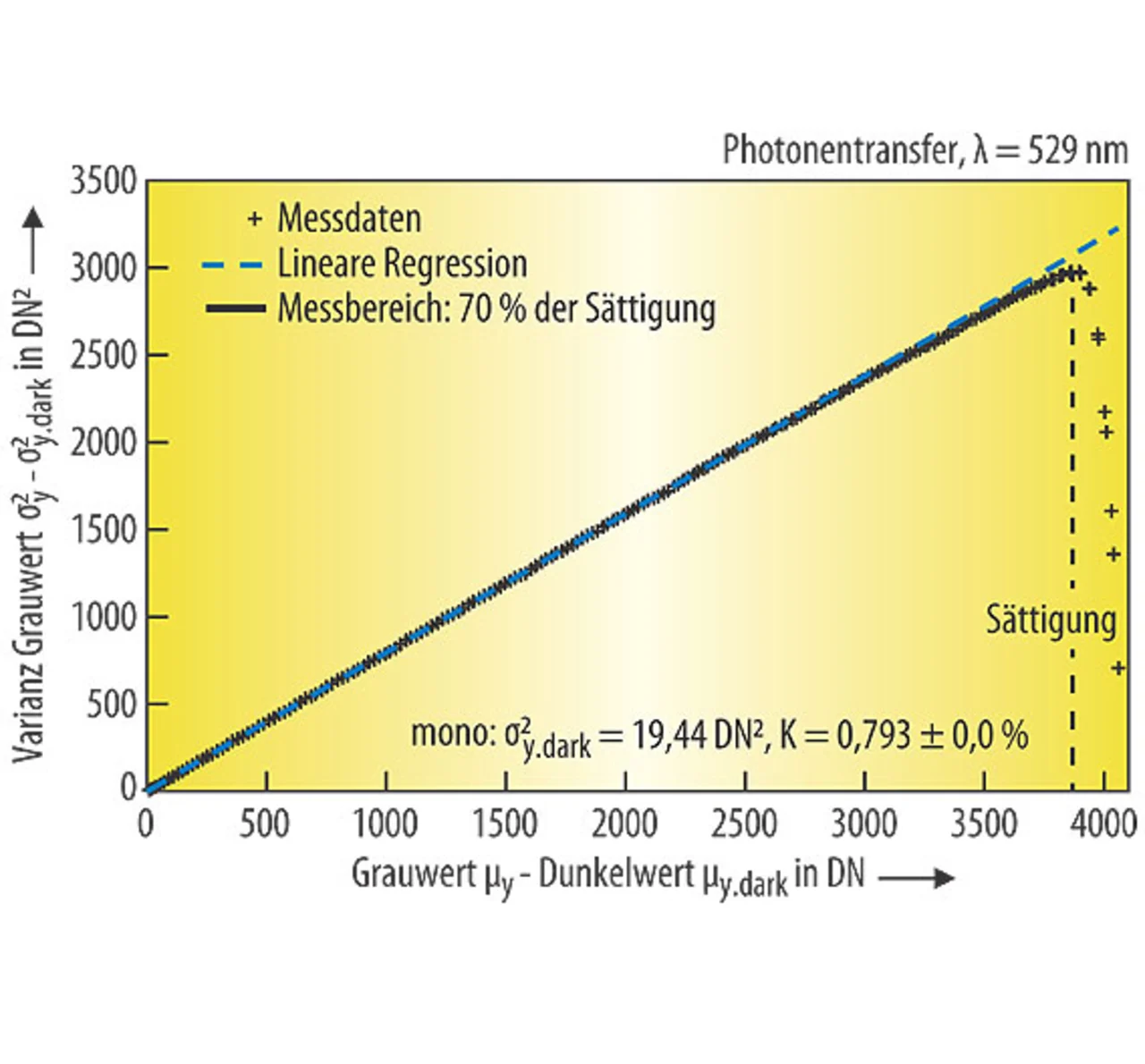
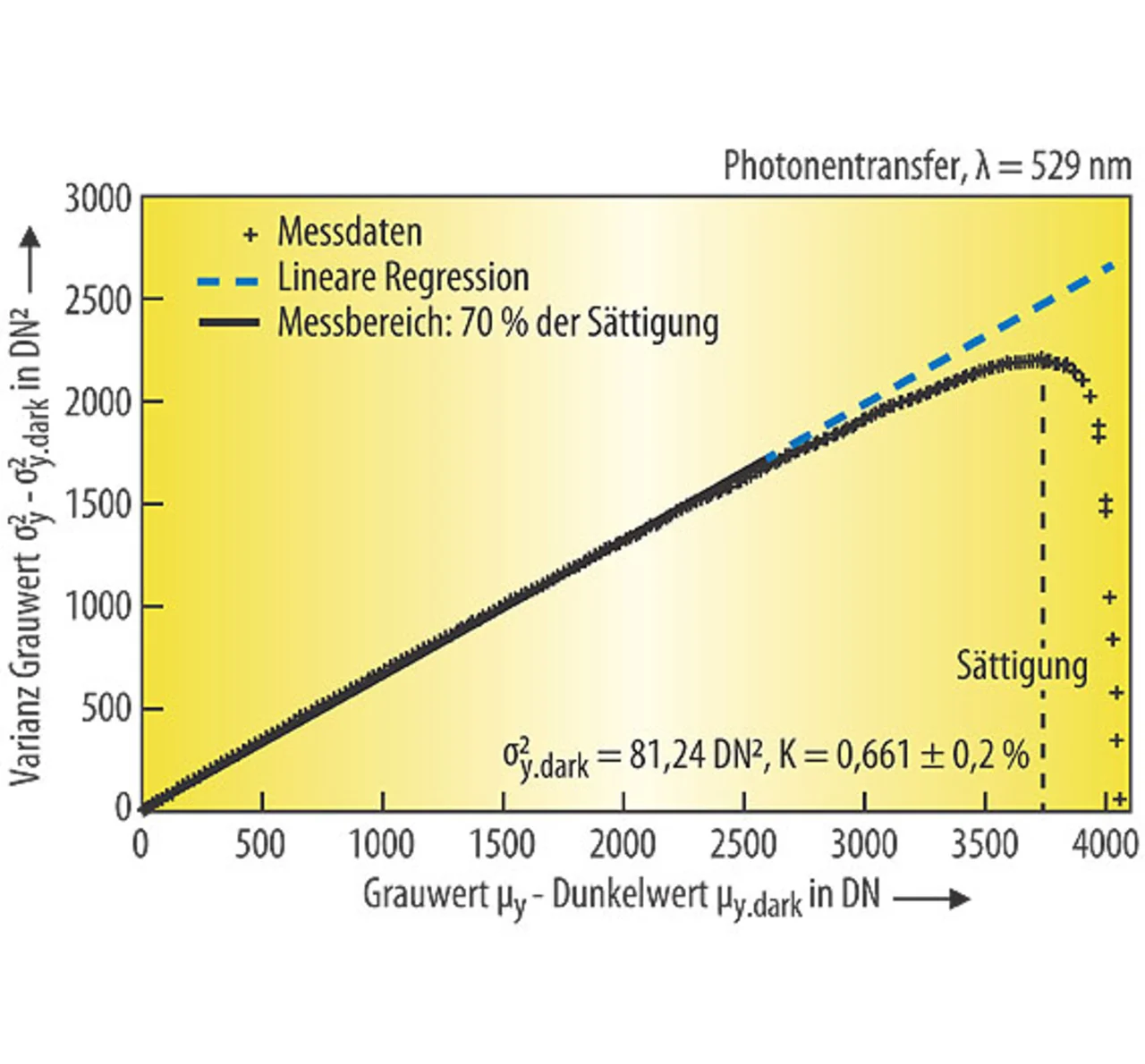
ergibt. Die Varianz steigt damit linear zum photonen-induzierten Grauwert an. Rauschen ist ausnahmsweise einmal für etwas gut: Aus der Steigung ergibt sich dann ohne jegliche Kenntnisse über die Kameraelektronik der absolute Verstärkungsfaktor K und aus dem Achsenabschnitt nach Abzug des Quantisierungsrauschens die Varianz des Dunkelrauschens σ_d².

Mit bekanntem Verstärkungsfaktor K kann aus der Steigung der Kamerakennlinie in Gleichung (3) auch die Quantenausbeute berechnet werden.

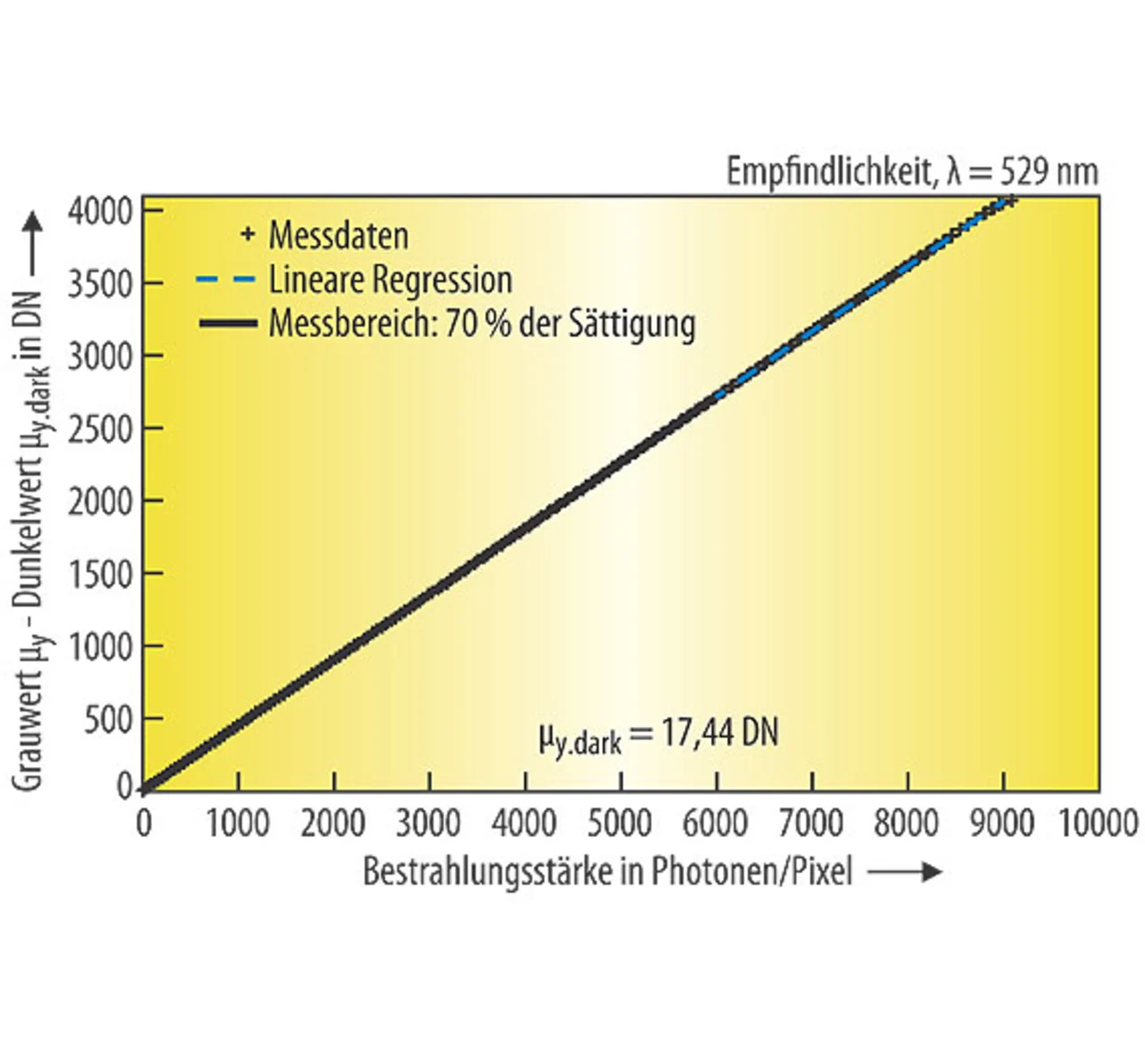
Diese Methode wird nach der Originalpublikation von Janesick [4] die Photontransfermethode genannt. Reale Kameras stimmen mit dem linearen Kameramodell überein (Bilder 2 - 5) und belegen daher, wie gut der modellbasierte Ansatz des Standards 1288 ist.

1. Der Standard EMVA 1288
2. Lineares Kameramodell
3. SNR und abgeleitete Parameter
4. Dunkelstrom

Lesen Sie mehr zum Thema

Weitere Artikel zu Sensoren & -systeme

Sie wurde 94 Jahre alt

Kübler-Gruppe trauert um Erika Kübler

Health Electronics Summit 2025

Smarte Sensorik gestaltet die Medizin von Morgen

Auszeichnung für Dr. Thorsten Sieß

Aachener Ingenieurpreis für die kleinste Herzpumpe

Übernahme in der Kraftsensorik

Baumer übernimmt X-Sensors

New Yole Group Report

Thermal imaging and sensing industry hit $7 billion in 2024

Weitere Artikel zu Kameras

IDS Imaging Development Systems

Kamera für KI-Anwendungen

ISO-Arbeitsgruppe für die Transformation

Aus der EMVA 1288 wird die ISO 24942

Adasky

Wärmebildkamera: eine echte Alternative zum teuren LiDAR

Schnelle Bewegungen effizient erfassen

IDS stellt Kamera mit Event-basiertem Sensor vor

2D/3D-Vision in Makro- und Mikroskopie

Kleine Details präzise messen und analysieren