Charakterisierung von Bildsensoren und Kameras
Der Standard EMVA 1288
Fortsetzung des Artikels von Teil 2
SNR und abgeleitete Parameter
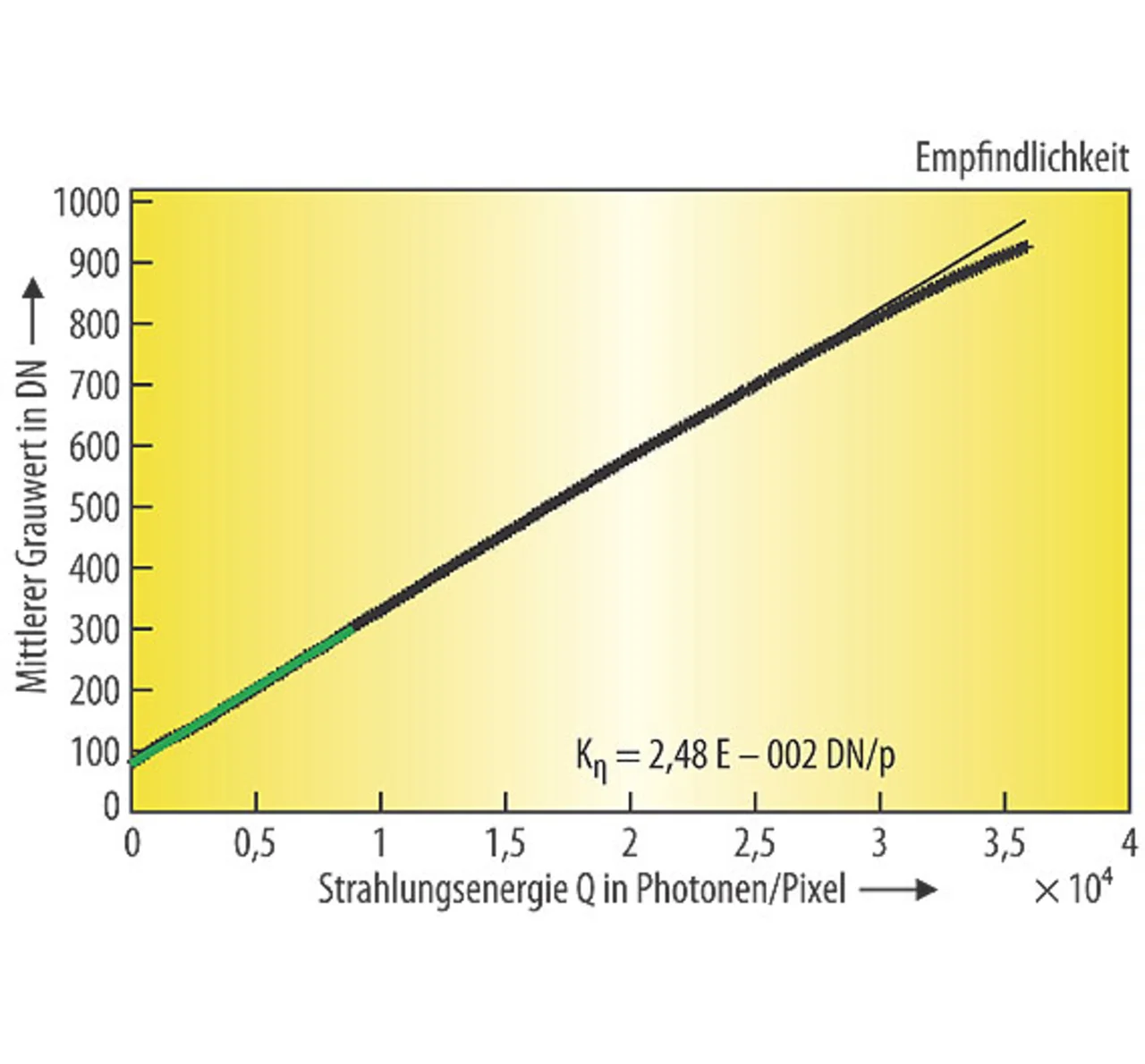
Umgekehrt ausgedrückt: Abweichungen in der Kamerakennlinie und insbesondere der Photontransferkurve zeigen klar Sensordefizite (Bilder 6 und 7).
SNR und abgeleitete Parameter
Der zentrale Parameter für die qualitative Bestimmung eines Kamerasignals ist das Signal-Rausch-Verhältnis:

Mit Hilfe der Kamerakennlinie und der Photontransferkurve kann das SNR als Funktion der Bestrahlungsstärke in Einheiten Photonenzahl/Pixel μp ausgedrückt werden:

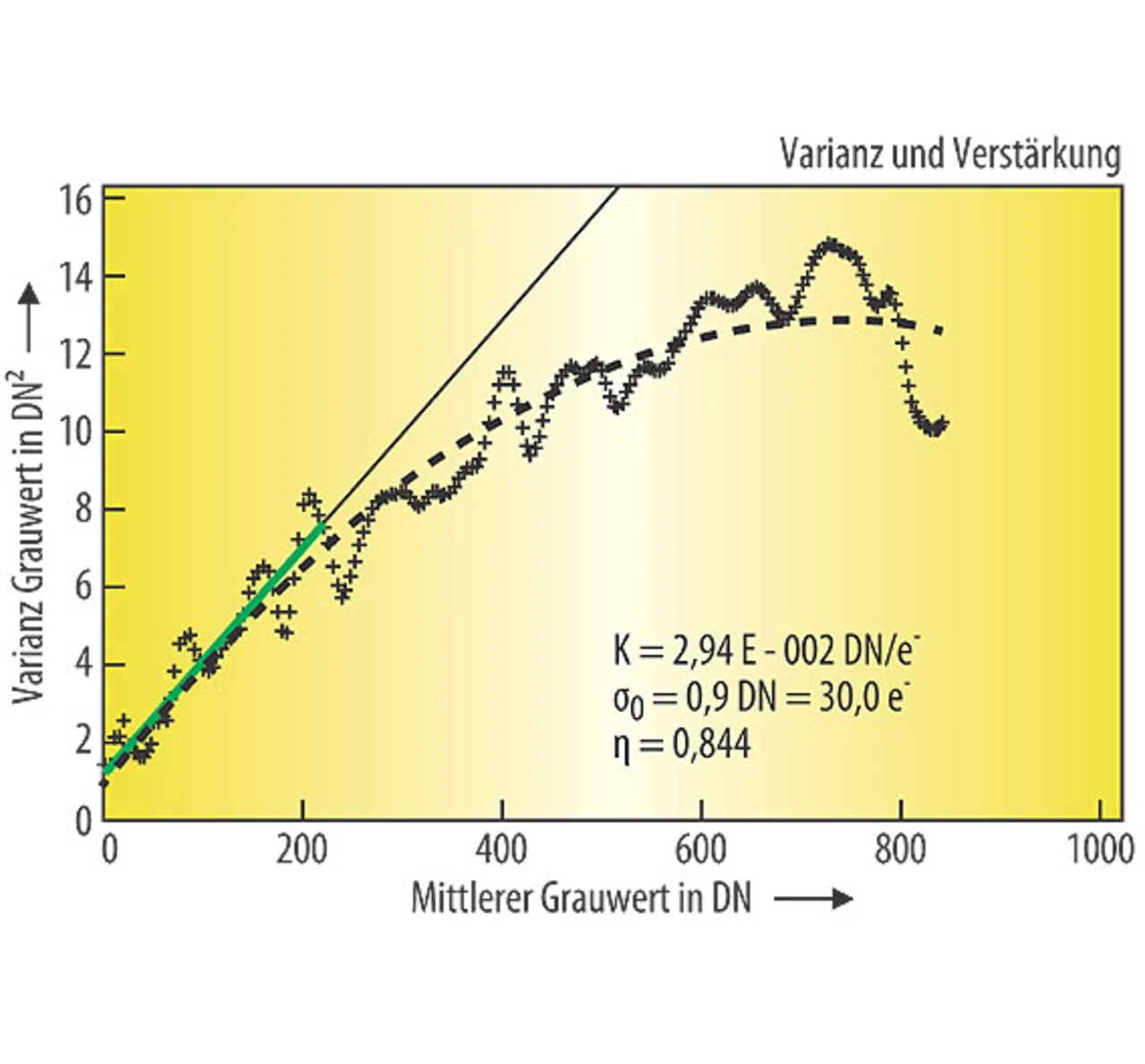
Unter Vernachlässigung des Quantisierungsrauschens hängt das SNR nicht von der Kameraverstärkung K ab, da Rauschen und Signal bei einer linearen Kennlinie gleichermaßen verstärkt werden.
Die kompliziert aussehende Formel wird verständlicher, wenn die Grenzfälle von viel und wenig Licht betrachtet werden. Dann ergibt sich

Diese Gleichungen besagen, dass das SNR bei kleinem Signal bzw. hohem Dunkelrauschen zuerst linear mit der Bestrahlung anwächst, bei hoher Bestrahlungsstärke aber nur noch mit der Wurzel der Bestrahlung. In einer doppelt-logarithmischen Darstellung ändert sich die Steigung daher von 1 auf 0,5 (Bild 8).
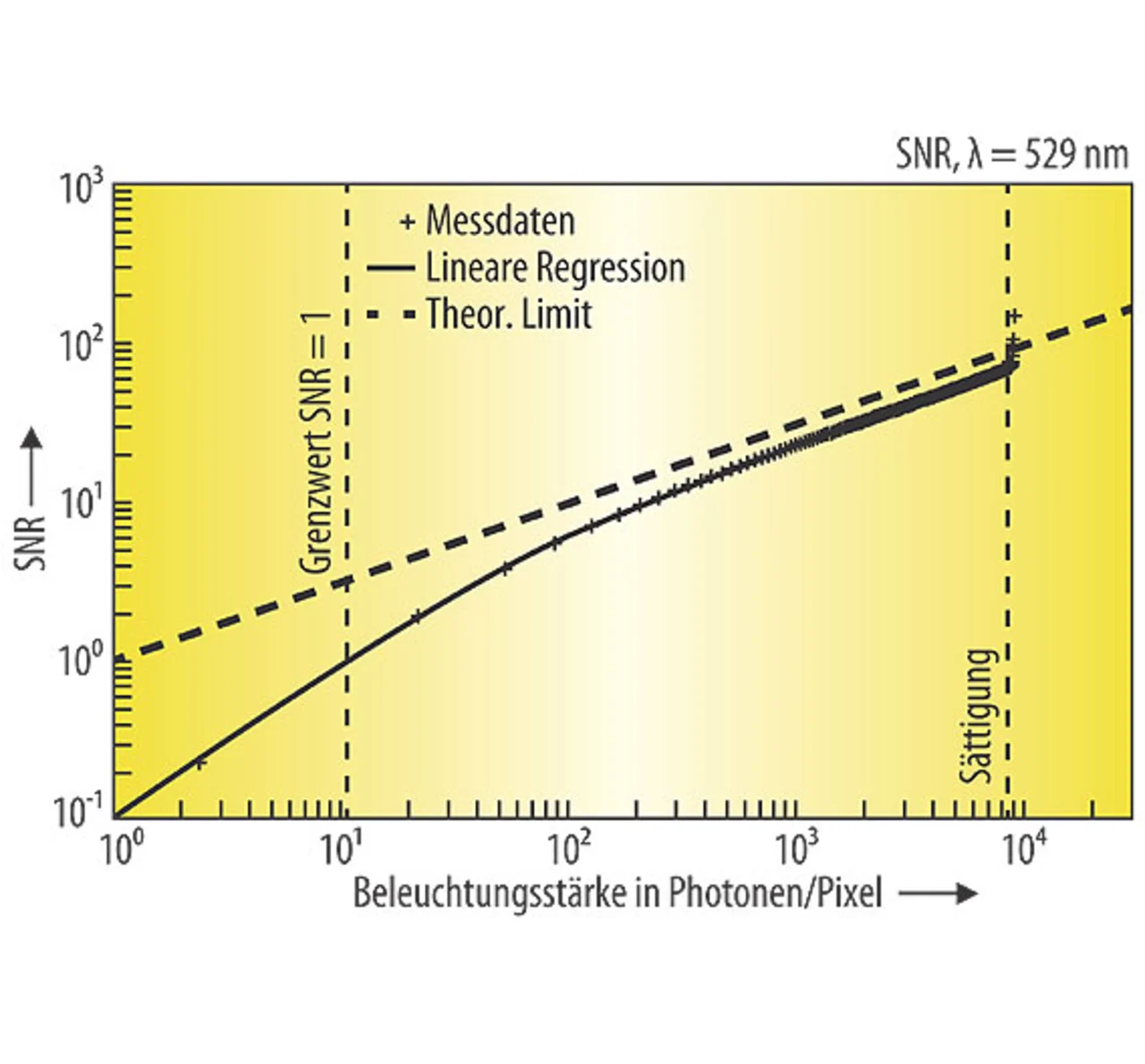
Es ist leicht möglich, die Werte für den bestmöglichen Sensor anzugeben: Dieser hat eine Quantenausbeute von Eins und kein Dunkelrauschen und ist damit nach Gleichung (10)

Bei viel Licht ist ein realer Sensor im SNR nur um den Faktor η(λ)1/2 geringer; bei wenig Licht hängt die Verschlechterung vom Dunkelrauschen ab und das SNR ist gegenüber einem idealen Sensor um den Faktor (η(λ) · μp1/2) / σd wesentlich geringer.
Aus der SNR-Kurve lassen sich alle weiteren sekundären Parameter ableiten, die mittlere Eigenschaften des Bildsensors beschreiben. Als Beispiel sind hier die Sättigungskapazität, die Empfindlichkeitsschwelle und der Signalumfang (DR) beschrieben. In der Praxis kann die sogenannte „full-well capacity“ , d.h. wie viele Ladungsträger ein Bildsensor maximal speichern kann, nicht gemessen werden, da das Bildsignal vorher durch den Spannungsbereich des A/D-Wandlers begrenzt wird. Daher wird eine Sättigungskapazität μp.sat gemessen. Man nimmt dafür den digitalen Grauwert, bei dem die Verteilung um diesen Grauwert noch nicht nach oben abgeschnitten wird. Als zuverlässiges Maß dafür hat sich der mittlere Grauwert μy mit der maximalen Varianz σy ergeben. Die Grauwertvarianz steigt ja linear mit dem Grauwert an und fällt dann scharf ab, wenn die Grauwertverteilung abgeschnitten wird (Bilder 3 und 5). Die Sättigungskapazität ist daher ein praktisches Maß für die maximale Photonenzahl, die ein Sensor pro Pixel messen kann. Aus der Umkehrfunktion zu Gleichung (10) ergibt sich die minimale Photonenzahl, die ein Bildsensor messen kann, die Empfindlichkeitsschwelle μp.min (absolute sensitivity threshold). Diese ist definiert durch die Photonenzahl (Bestrahlung), bei der das SNR Eins ist. Diese ergibt sich aus Gl. (10) zu

Der Signalumfang (dynamic range DR) ist das Verhältnis von Sättigungskapazität zur Empfindlichkeitsschwelle:

und wird im 1288-Standard als direktes Verhältnis in dB-Wert (20 log10 DR) und in Bits (log2 DR) angegeben. Die Parameter können auch graphisch aus der doppelt-logarithmischen SNR-Kurve abgelesen werden (Bild 8).
- Der Standard EMVA 1288
- Lineares Kameramodell
- SNR und abgeleitete Parameter
- Dunkelstrom



