Oszilloskope
Zeit fürs Upgrade?
Beim Kauf eines Oszilloskops zum Testen neuer Designs gilt der erste Blick der Bandbreite, der zweite dem Preisschild. Bedauerlicherweise sind diese beiden Maßzahlen linear miteinander korreliert. Wiee lässt sich bestimmen, wie viel Bandbreite für die aktuellen Entwicklungsprojekte ausreicht und wann es Zeit für ein Oszilloskop-Upgrade ist?
Die meisten heutigen Embedded-Designs sind Mixed-Signal-Designs, die sowohl analoge als auch digitale Signale umfassen. Die erforderliche Bandbreite eines Oszilloskops ergibt sich meist aus der Maximalgeschwindigkeit der digitalen Signale der CPU des Systems (Taktfrequenz und Flankenzeiten). Oft ist auch die zeitliche Spezifikation des Speichers zu berücksichtigen. Am häufigsten kommt heute DDR-Speicher zum Einsatz, eine Speicherbauart, die sowohl auf der ansteigenden als auch der abfallenden Taktflanke Daten überträgt.
Angenommen, das letzte Designprojekt eines Embedded Systems war mit DDR1-Speicher aufgebaut, und zwar mit Speichertransferraten um die 200 MBit/s. Um die wesentlichen Zeitparameter von CPU und Speichersubsystem zu erfassen und zu verifizieren, arbeitete man mit einem 500-MHz-Oszilloskop, das für diesen Anwendungszweck auch genau genug war. Das nächste Projekt arbeitet aber mit schnellerem DDR2-Speicher. Braucht man dafür ein Oszilloskop mit größerer Bandbreite? Wenn ja, wie groß sollte diese Bandbreite sein?
Augendiagramm eines DDR2-667-Datensignals
Jobangebote+ passend zum Thema
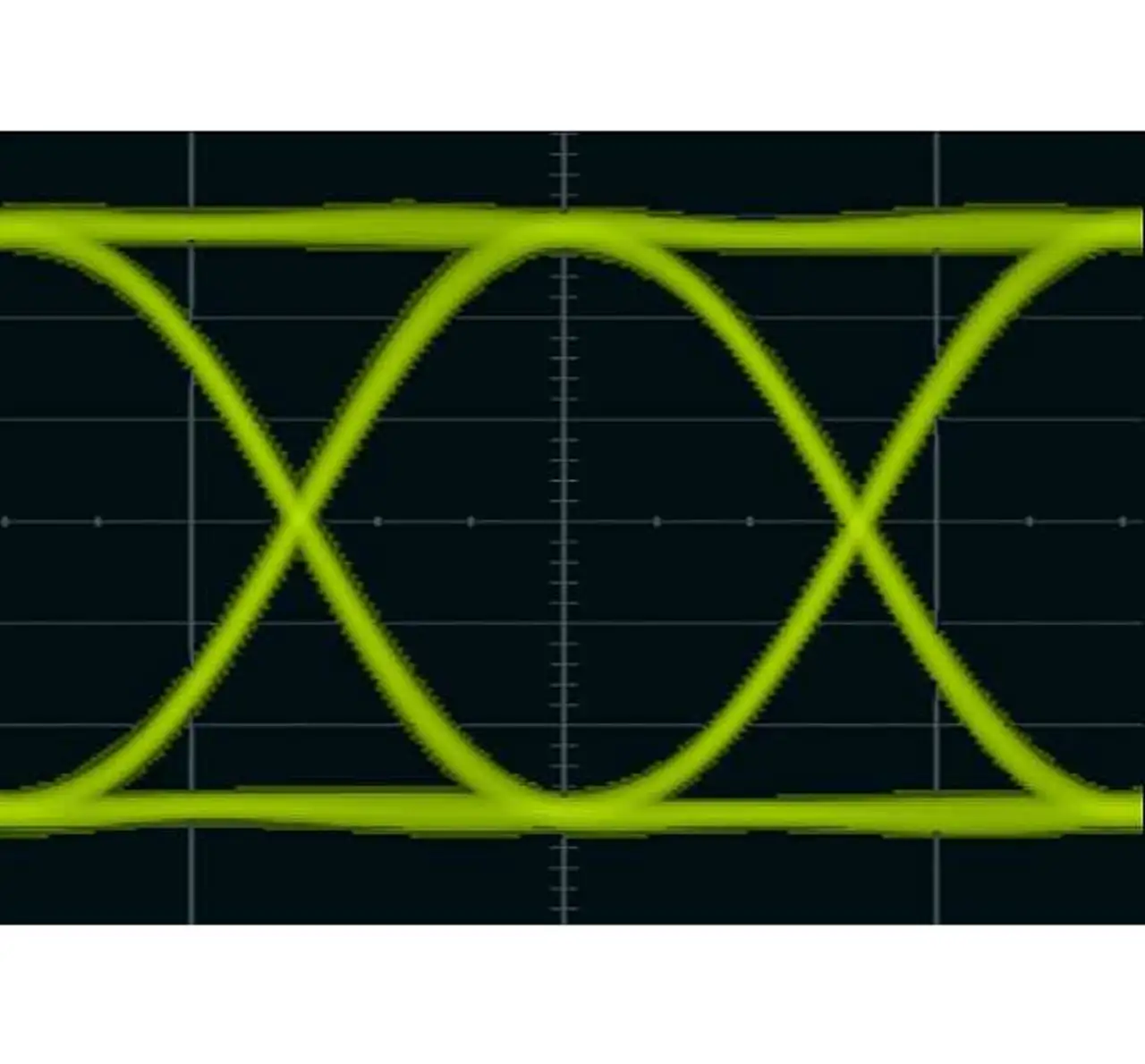
Eine gängige Messung an Schreib- und Lesesignalen von DDR-Speicher ist die Erfassung eines Augendiagramms. Augendiagramme auf einem Oszilloskop liefern ein Bild der Signalqualität, indem sie »0«- und »1«-Bits überlagern und anzeigen, wann Daten gültig sind. Bild 1 zeigt ein Beispiel für ein Augendiagramm eines Datensignals eines DDR2-667-Speichers, gemessen mit einem Oszilloskop »MSOX3054A« von Agilent mit einer Bandbreite von 500 MHz. Die Schreib/Lesefrequenz eines DDR2-667-Speichers beträgt 667 MHz, dabei werden sowohl auf der ansteigenden als auch auf der abfallenden Flanke des Taktes Daten übertragen.
Das Taktsignal selbst hat also 333 MHz. Obwohl die maximal spezifizierte Datenrate dieses Speichertyps 667 MBit/s beträgt, liegt die Schrittgeschwindigkeit der Daten auch nur bei 333 MHz (nämlich bei einem Datenmuster 1-0-1-0-1 ...). Man könnte daher annehmen, dass für einen Takt von 333 MHz und eine Schrittgeschwindigkeit der Daten von 333 MHz für genaue Messungen ein Oszilloskop mit 500 MHz Bandbreite ausreicht.
In Bild 1 ist jedoch zu erkennen, dass ein 500-MHz-Oszilloskop aus den Rechteckimpulsen der Daten so etwas wie Sinuskurven macht. Ein 500-MHz-Oszilloskop kann in diesem Fall nicht viel mehr als die Grundfrequenz darstellen (also die 1. Harmonische).
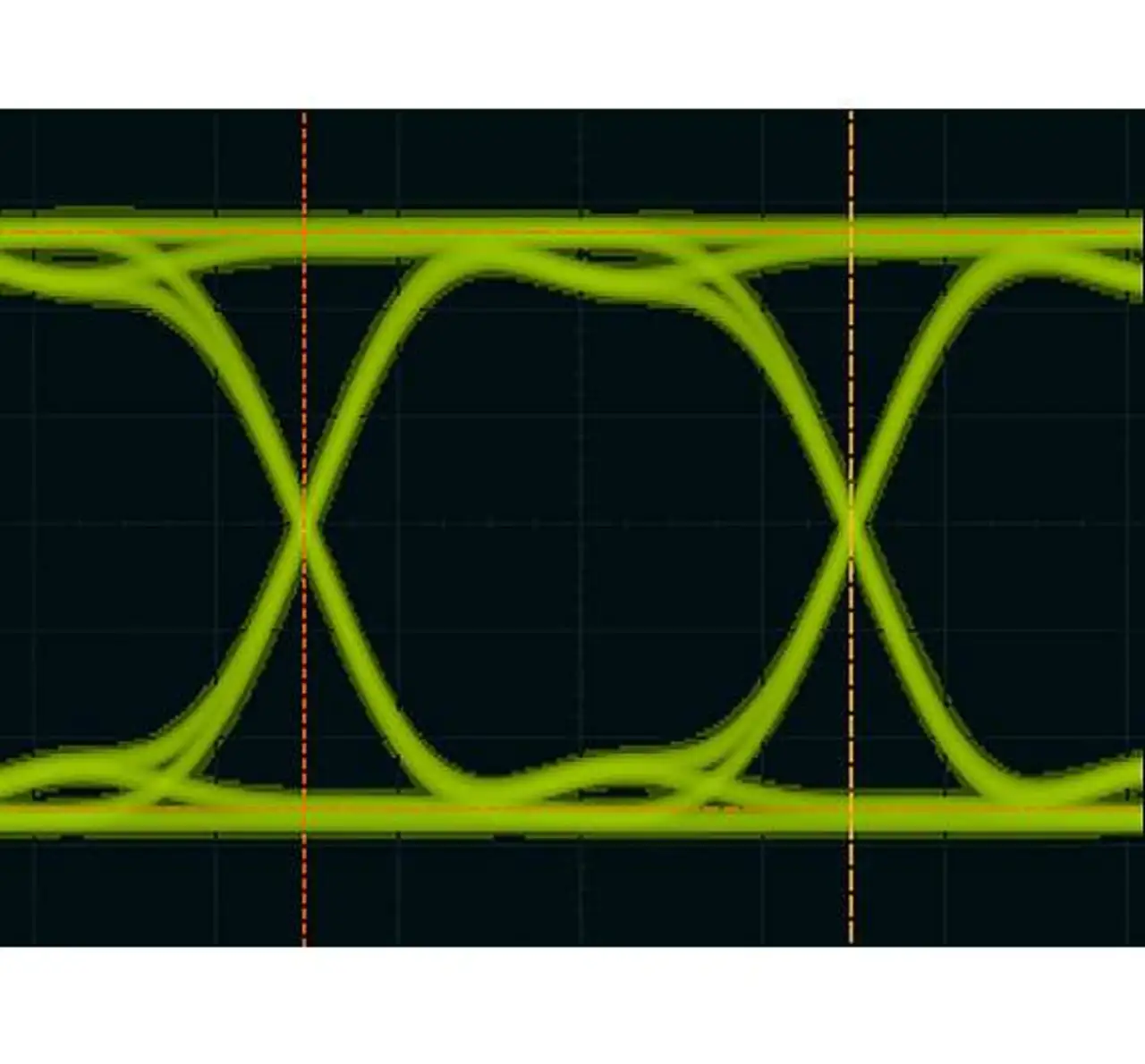
Aus diesem Grund sehen die Signale so sinus-ähnlich aus. Ein 500-MHz-Oszilloskop reicht für solche Signale somit nicht. Bild 2 zeigt ein Augendiagramm desselben DDR2-667-Datensignals, dieses Mal aber mit dem neuen Oszilloskop »MSOX3104A« desselben Herstellers erfasst, das eine spezifizierte Bandbreite von 1 GHz aufweist. Man sieht unmittelbar, dass die Darstellung des breitbandigeren Oszilloskops schärfer ist und mehr Details zeigt. Wenn also ein solches Signal zu messen ist, ist es Zeit für den Schritt hin zu 1 GHz Bandbreite.
Ermittlung der nötigen Bandbreite
In digitalen Anwendungen hängt die erforderliche Bandbreite des Oszilloskops von der schnellsten Signalflanke im Testobjekt ab, die zu messen ist. Wenn diese Größe erst einmal bekannt ist, lässt sich die Anstiegszeit in eine Frequenz umrechnen, die hier als fMAX bezeichnet ist. Dieser Wert darf allerdings nicht mit der fMAX verwechselt werden, die sich aus dem Nyquist-Theorem ergibt. Hier bietet sich der Begriff der »praktikablen Maximalfrequenz« an, weil schnelle Flanken theoretisch aus einem unendlichen Spektrum von Frequenzen bestehen. Allerdings tragen die höheren Harmonischen nur wenig zur Form einer schnellen Flanke bei.
Aus einer bekannten fMAX lässt sich also die erforderliche Bandbreite bestimmen. Wie bestimmt man nun aber die schnellste Flanke? Offenbar handelt es sich hier um ein Henne-Ei-Problem. Digitalschaltungen in heutigen Designs haben typischerweise eine Zeitspezifikation für ihre Ein- und Ausgänge. Diese spezifizierten Anstiegszeiten (RT, Rise Time) orientieren sich traditionell an 10% und 90% des Nennpegels. Hat man erst einmal die schnellsten Anstiegszeiten in einem Design ermittelt, errechnet sich fMAX nach einer der folgenden einfachen Formeln:

Für manche Bauteile ist eine maximale Slew-Rate (SR) spezifiziert (und nicht eine bestimmte Anstiegszeit). Das gilt etwa für die meisten DDR-Speicher. In diesem Fall lässt sich die Anstiegszeit von 20% bis 80% nach folgender Formel näherungsweise berechnen:

Ist fMAX erst einmal ermittelt, kann ein Oszilloskop mit dieser Bandbreite dazu dienen, Signale mit dieser Frequenz mit hinreichender Genauigkeit zu erfassen (also mit vielleicht 20% Fehler) und ihre Anstiegszeiten zu messen. Wer allerdings Anstiegszeiten mit 5% Genauigkeit messen möchte, braucht ein Oszilloskop mit einer spezifizierten Bandbreite, die um den Faktor 1,5 bis 2 über fMAX liegt. Dies zeigt das folgende einfache Beispiel:
Angenommen, der Entwickler hat die schnellste Anstiegszeit im System mit 800 ps ermittelt (20%- bis 80%-Schwelle). fMAX beträgt dann 0,4/800 ps = 500 MHz. Wenn das Messgerätebudget eng ist und 20% Messfehler tolerabel sind, kann ein Oszilloskop mit 500 MHz Bandbreite diese Messung durchführen. Anders gesagt: Will man eine Anstiegszeit von 800 ps messen, misst dieses Oszilloskop irgendwas im Bereich von 1 ns. Braucht man höhere Genauigkeit, ist ein 1-GHz-Oszilloskop die bessere Wahl. Neuere Messinstrumente, etwa aus der Oszilloskopfamilie »3000 X« von Agilent, bieten die Möglichkeit des Upgrades. So lässt sich die Bandbreite beispielsweise von 100-MHz-Geräten nachträglich auf 1 GHz erweitern. Die Leistung dieser Oszilloskope wächst somit mit den Messanforderungen mit.
Über die Autoren:
Johnnie Hancock ist Marketing Engineer, Peter Kasenbacher ist Product Line Manager EMEA für Oszilloskope, beide bei Agilent.