Effiziente Abbildung von Audio-Algorithmen in Programmierbarer Logik und ASICs
Rock ’n’ Roll im FPGA #####
Fortsetzung des Artikels von Teil 5
Rock ’n’ Roll im FPGA

Jobangebote+ passend zum Thema
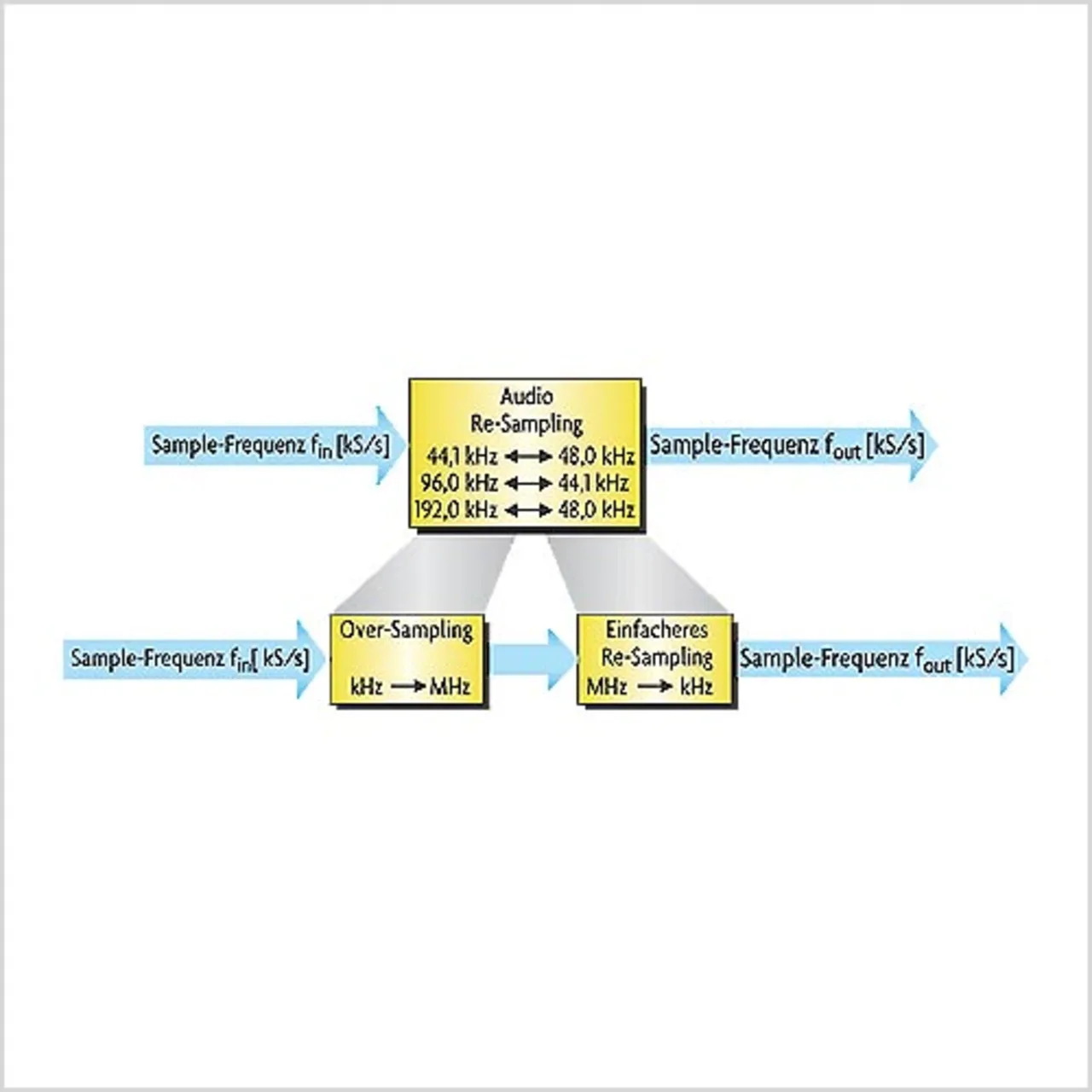
Der Algorithmus beinhaltet zwei Schritte
Um Signale mit unterschiedlichen Sample-Rates verarbeiten zu können, muss eine Konvertierung vorgenommen werden. An dieser Stelle sei nochmals daran erinnert, dass Audiosignale üblicherweise Sample-Rates von 44,1 kHz (CD Sample Rate) oder 48 kHz (DAT) aufweisen. Zur Konvertierung der Frequenzen (Asynchrones Re-Sampling) wird mit einer Polyphase-FIR-Filter-Struktur gearbeitet. Der Algorithmus beinhaltet zwei Schritte (Bild 2). Im ersten Schritt erfolgt das Oversampling der Frequenzen. Der zweite Schritt – lineare Interpolation – ist notwendig, um aus einer beliebigen Frequenz eine beliebige andere Frequenz zu generieren. Die beiden Frequenzen sind zueinander asynchron. Das Re-Sampling des Signals in einem einzigen Schritt würde erheblich mehr Ressourcen benötigen, da ein solches Filter entsprechend komplex ausfällt. Aus einer solchen Implementierung können mehrere Millionen Multiplikationen resultieren. Eine derartige Beschreibung ist nicht effizient und muss vermieden werden. Wird für den zweiten Schritt eine lineare Interpolation implementiert, resultieren daraus wesentlich einfachere Strukturen.
Der erste Schritt, das Oversampling, muss ebenfalls in einer möglichst effizienten Art und Weise beschrieben werden. Nur so kann man eine ressourcenschonende Abbildung im FPGA ermöglichen. Die Anzahl der insgesamt benötigten Rechenoperationen kann weiter drastisch reduziert werden, wenn dieser Schaltungsteil in mehreren, kaskadierten Stufen anstatt einer einzigen Berechnung durchgeführt wird. Bei der Implementierung des Algorithmus ist bereits darauf zu achten, welche Zielarchitektur (DSP, FPGA) die Berechnung durchführen wird. FPGAs sind – anders als Digitale Signalprozessoren – bei der Implementierung vieler Einzelmultiplikationen durch ihre Ressourcen limitiert. Mit der Ordnung des Filters steigt linear auch die Anzahl der benötigten Multiplizierer. Aus jedem „Tap“ des Filters resultiert die Nutzung eines DSPBlocks oder 18×18-Multiplizierers. Bei einer Kaskadierung der Re-Sampling-Stufen muss jedes einzelne Filter sehr viel weniger komplexe Funktionen erfüllen.
In der Theorie resultiert dementsprechend eine optimale Implementierung des Filters aus so vielen einzelnen Stufen wie möglich. Die mathematische Herleitung der Reduzierung von Rechenoperationen ist in der entsprechenden Fachliteratur ausführlich dargestellt und soll nicht Inhalt dieses Artikels sein. In der Praxis zeigt sich jedoch, dass die Kaskadierung der Re-Sampling Stufen durchaus notwendig ist, aber die Anzahl der Kaskaden begrenzt werden muss. Werden zu viele kaskadierte Stufen eingeführt, steigt die Zahl der benötigten Ressourcen wieder an, da bei der Implementierung zusätzliche Logik eingeführt wird. Wird als Zielarchitektur ein FPGA genutzt, hat sich die Zahl „2“ für die Einzelschritte des Oversampling als optimal erwiesen. Die gesamte Schaltung besteht dementsprechend aus zwei relativ einfachen Filtern für das Oversampling und einer einfachen linearen Interpolation. Diese Struktur lässt sich effizient auf ein FPGA abbilden.
- Rock ’n’ Roll im FPGA #####
- Rock ’n’ Roll im FPGA
- Rock ’n’ Roll im FPGA
- Rock ’n’ Roll im FPGA
- Rock ’n’ Roll im FPGA
- Rock ’n’ Roll im FPGA
- Rock ’n’ Roll im FPGA