EMV-Simulation mit LTspice
Verbesserung der Signalintegrität
Fortsetzung des Artikels von Teil 1
Bewertung der Konformität über den Toleranzbereich
Die in den Beispielschaltungen verwendeten Bauelemente weisen große Toleranzen auf, und mithilfe von Berechnungen lässt sich überprüfen, ob diese Toleranzen problematisch sein werden. Wenn eine Schaltung allerdings Hunderte von Bauteilen enthält, sind manuelle Verfahren mit Stift und Papier oder auch mit einem Tabellenkalkulationsprogramm sehr zeitaufwändig, und wichtige Parameter werden dabei möglicherweise nicht erfasst. Einige Bauelemente können durchaus mit geringerer Toleranz verfügbar sein, aber wenn sämtliche Bauteile mit geringer Toleranz beschafft werden sollen, können sich Kosten- und Verfügbarkeitsprobleme einstellen. Hinzu kommt, dass Alterungs- und Temperatureinflüsse dann immer noch unberücksichtigt bleiben.
Jobangebote+ passend zum Thema
Spice bzw. LTspice haben jedoch beeindruckende Fähigkeiten mit, um Schaltungen über ihre Toleranzen zu validieren.
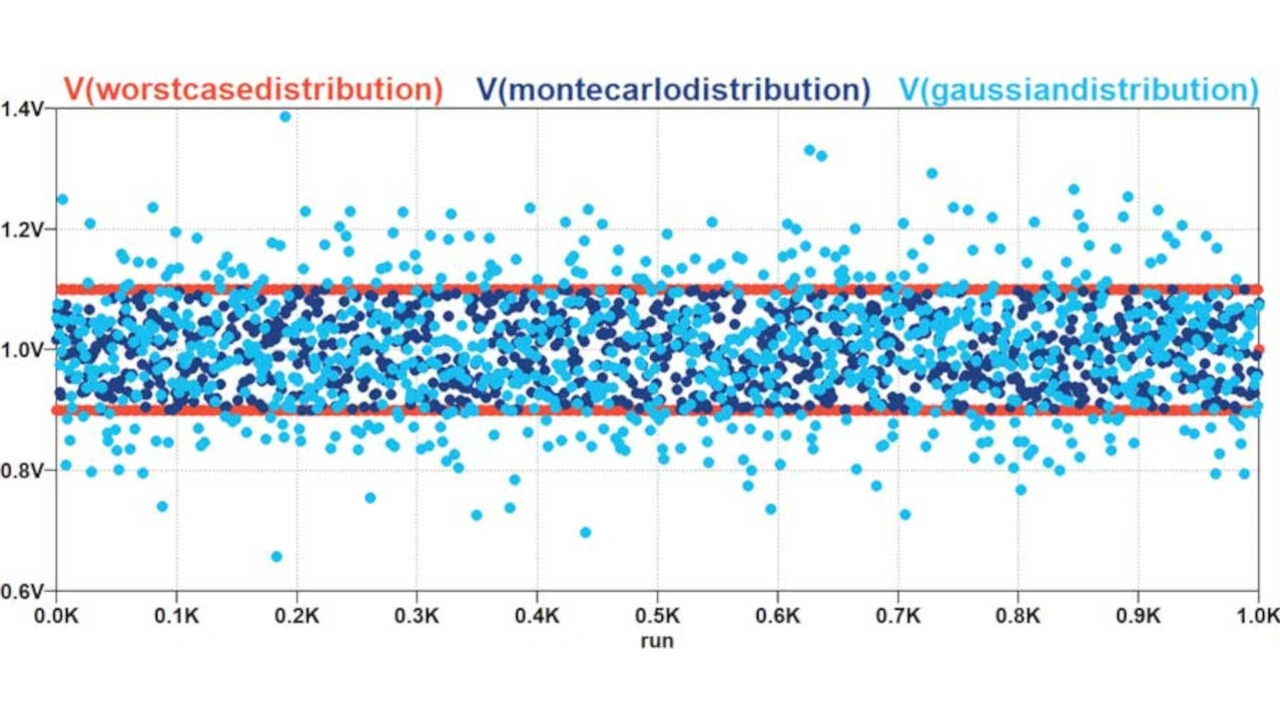
In den folgenden Abschnitten werden Techniken zur Toleranzanalyse nach dem Monte-Carlo-Verfahren und der Gaußschen Normalverteilung ebenso beschrieben wie die in LTspice enthaltene Worst-Case-Analyse (Bild 20).
Gemeinsame Prüfschaltung für Gaußsche Normalverteilung, Monte Carlo und Worst Case
Um die Relevanz und Gründlichkeit in einem realen Anwendungsfall vergleichen zu können, wird das nachfolgend beschriebene Beispiel auf Basis der Arbeit von Graber [3] genutzt. Es handelt sich dabei um eine Simulationsschaltung für die Bit-Übertragungsschicht (MDI) des Single-Pair-Ethernet-Standards (SPE) 10BASE-T1L (10SPE).
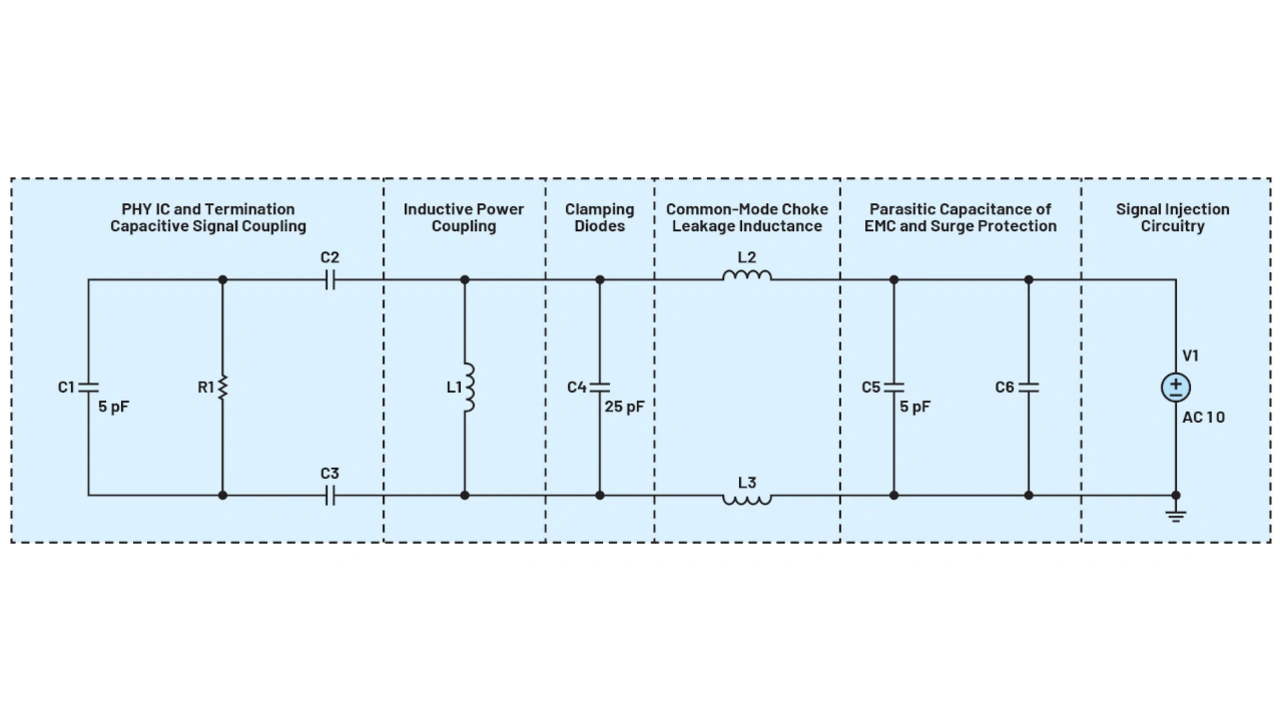
Die in Bild 21 gezeigte Simulationsschaltung enthält einen Abschlusswiderstand von 100 Ω ±10 % für den 10BASE-T1L Ethernet PHY/MAC-PHY des Typs ADIN1110 oder ADIN1100 von Analog Devices.
Modelliert werden die Signalkopplungs-Kapazität, die Induktivitäten zur Stromversorgungs-Kopplung, die Gleichtaktdrossel und weitere EMI-Schutzbausteine. Für einige Bauteile sind der empfohlene Wert und der Toleranzbereich angegeben.
Die Syntax für die Rückflussdämpfungs-Darstellung lautet wie folgt:
Monte-Carlo-Simulation
Eine Monte-Carlo-Simulation verwendet einen zufällig gewählten Wert aus dem Toleranzbereich jedes spezifizierten Bauteils der Simulationsschaltung. Alle Werte innerhalb des Toleranzbereichs der Bauelemente haben die gleiche Wahrscheinlichkeit, in der Schaltungssimulation verwendet zu werden.
| Bauelement | Bereich | Syntax des Bauteilwerts (Monte Carlo) |
|---|---|---|
| R1 | 90 Ω bis 110 Ω | {mc(100, ToIA)} |
| C2, C3 | 200 nF bis 600 nF | {mc(400 nF, ToIB)} |
| L1 | 500 μH bis 1500 µH | {mc(1000 µH, ToIC)} |
| L2, L3 | 0 nH bis 500 nH | {mc(250 nH, ToID)} |
| C6 | 0 pF bis 200pF | {mc(100 pF, ToIE)} |
Tabelle 1. Definition von Bauteilwerten und Toleranzen mithilfe der Monte-Carlo-Methode. (Quelle: Analog Devices)
LTspice enthält eine komfortable Monte-Carlo-Funktion mit einfacher Syntax. Im Fall eines 100-Ω-Widerstands mit 10 % Toleranz lautet diese beispielsweise:
{mc(100R, ToIA)}
.param ToIA = 0.10
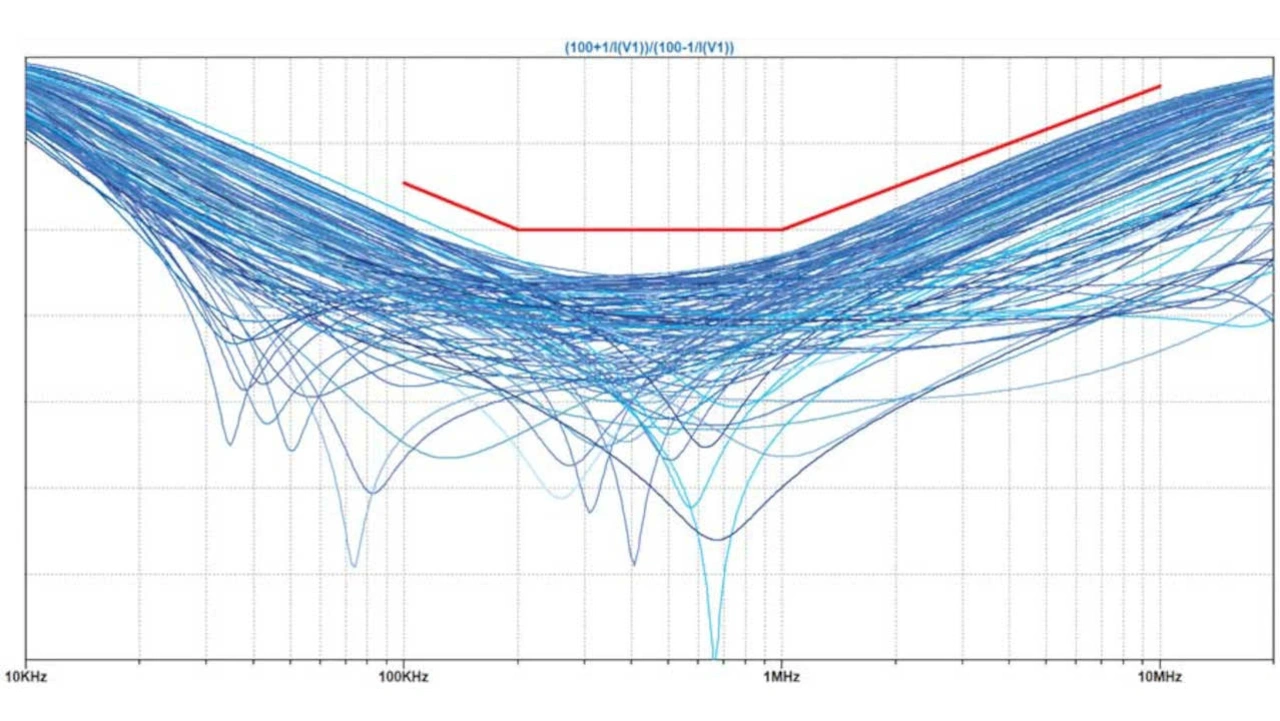
Die in Bild 21 beschriebene Schaltung [3] eignet sich zur Simulation der Rückflussdämpfung, die ein Maß für alle wahrscheinlich auftretenden Signalreflexionen ist. Hervorgerufen wird die Rückflussdämpfung durch Impedanz-Fehlanpassungen an verschiedenen Punkten einer Kabelverbindung. Sie wird in Dezibel angegeben und ist von besonderer Relevanz für die hohen Datenraten und langen Kabelverbindungen (1.700 m) von 10BASE-T1L.

In die Darstellung muss jetzt nur noch die Grenzlinie für die MDI-Rückflussdämpfung (rote Linie in Bild 22) eingefügt werden. Im Plot-Settings-Menü wird dazu auf die Schaltfläche „Save Plot Settings“ geklickt.
Die .PLT-Datei wird mit einem herkömmlichen Texteditor geöffnet, um die Syntax für die Grenzlinie aus der Excel-Datei (Bild 23) einzufügen.
Damit Entwickler in ihren Simulationen identische Werte erhalten, müssen sie mit der rechten Maustaste auf den Signalverlauf und klicken auf die Schaltfläche „Don’t Plot Phase“.
Zusammenfassung der Monte-Carlo-Simulation
Die Monte-Carlo-Simulation ist eine sinnvolle Möglichkeit, die Konformität einer Elektronikschaltung über ihren Toleranzbereich zu bewerten. Mit großer Wahrscheinlichkeit wird sie den Anforderungen der meisten Entwickler gerecht, ohne die Anzahl der Simulationsdurchgänge ausufern zu lassen.
Worst-Case-Simulation
Die Worst-Case-Simulation ist keine eingebaute Funktion von LTspice, jedoch ist die Implementierung von Funktionen möglich, die eine Worst-Case-Simulation ergeben. Genaueres hierzu findet sich bei Joseph Spencer und Gabino Alonso [4].
Zur Ausführung von Simulationen nach dem Worst-Case-Szenario werden die beiden Funktionen .func binary(run,index) und .func wc(nom,tol,index) benötigt, die als SPICE-Direktiven in den LTspice-Schaltplan eingefügt werden müssen.
.func binary(run,index) floor(run/(2**index))-2*floor(run/(2**(index+1)))
.func wc(nom,tol,index) if(run==numruns,nom,if(binary(run,index),nom*(1+ tol),nom*(1-tol)))
Um diese Funktionen zu nutzen, sind verschiedene Maßnahmen erforderlich:
- Mithilfe von numruns ist die Anzahl der Simulationsdurchläufe anzugeben, die notwendig ist, um die Maximal-, Minimal- und Nominalwerte eines jeden Bauteils gemäß einer Worst-Case-Analyse abzudecken. Die Anzahl der Durchläufe beträgt 2N+1, wobei N die Zahl der verschiedenen mit den Bauteiltoleranzen zusammenhängenden Indizes angibt. In Bild 21 ergeben sich 129 Durchläufe (einschließlich Durchlauf 0), sodass die Syntax wie folgt lautet:
.param numruns = 129 - Anstelle eines regulären Bauteilwerts ist der folgende Ausdruck anzugeben:
{wc(100R, 0.1, 0)}
Darin ist 100R der Nennwert, 0.1 die Toleranz – in diesem Fall ±10 % – und 0 der Index des zu variierenden Parameters. Das nächste zu variierende Bauteil erhält den Index 1.
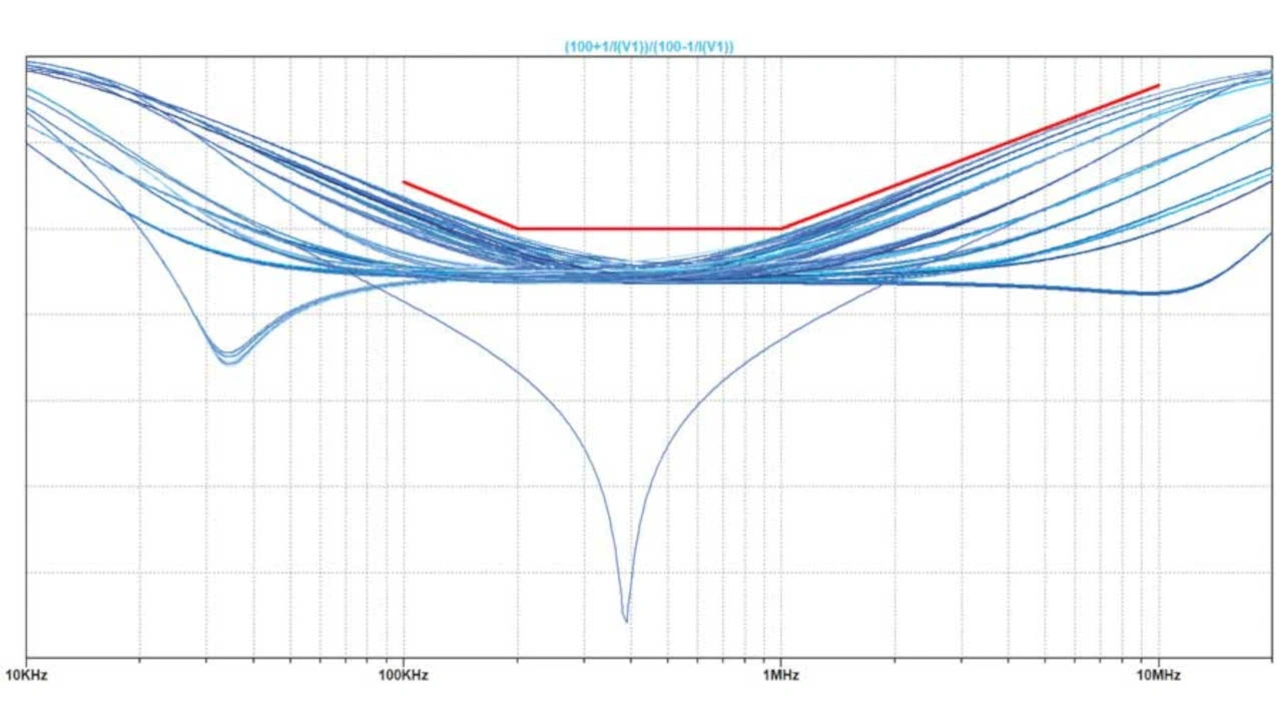
Die in Bild 21 gezeigte Simulationsschaltung wird nun anstelle statischer Bauteilwerte mit den Ausdrücken aus Tabelle 2 abgearbeitet.
Die Ergebnisse sind in Bild 24 zu sehen. Die Grenzlinie für die MDI-Rückflussdämpfung wird durch Editieren der Plot-Settings-Datei in der weiter oben beschriebenen Weise hinzugefügt.
|
Bauelement |
Bereich |
Syntax des Bauteilwerts (Worst Case) |
|---|---|---|
| R1 | 90 Ω bis 110 Ω | {wc(100, TolA, 0)} |
| C2 | 200 nF bis 600 nF | {wc(400 nF, TolB, 1)} |
| C3 | 200 nF bis 600 nF | {wc(400 nF, TolB, 2)} |
| L1 |
500 μH bis 1500 µH |
{wc(1000 µH , TolC, 3)} |
| L2 | 0 nH bis 500 nH | {wc(250 nH, TolD, 4)} |
| L3 | 0 nH bis 500 nH | {wc(250 nH, TolD, 5)} |
| C6 | 0 nH bis 500 nH | {wc(250 nH, TolD, 5)} |
Tabelle 2. Definition von Bauteilwerten und Toleranzen mithilfe der Worst-Case-Methode. (Quelle: Analog Devices)
Zusammenfassung der Worst-Case-Analyse
Bei Steve Knudtsen [5] findet sich eine knappe Übersicht über die Vorteile und Grenzen der Worst-Case-Analyse beim Systementwurf. Häufig angewandt wird diese Art der Analyse, wenn die Bauteilparameter bis an ihre maximale Toleranzgrenze ausgereizt werden. Zu den Nachteilen des Verfahrens gehören Ergebnisse, die nicht den üblicherweise beobachteten Resultaten entsprechen. Um ein System beobachten zu können, das tatsächlich das Worst-Case-Verhalten an den Tag legt, müsste eine sehr große Anzahl von Systemen gebaut werden. Soll ein System für Worst-Case-Bedingungen ausgelegt werden, kann die Verwendung sehr teurer Bauelemente erforderlich sein. Die Durchführung einer Worst-Case-Analyse im Verbund mit einer Monte-Carlo-Simulation kann jedoch wertvolle Erkenntnisse über das System liefern.
Die Worst-Case-Analyse eignet sich optimal für eine grobe Validierung des Verhaltens, wenn die Simulationen sehr lang dauern und das nominelle Verhalten bereits validiert wurde.
Gaußsche Simulation
Anpassungen nach dem Standardabweichungs-Parameter σ der Gaußschen Normalverteilung lassen sich mit den Ausdrücken in Tabelle 3 vornehmen.
| Verwendeter Ausdruck | Anteil der in den Toleranzbereich fallenden Werte |
|---|---|
| {nom*(1+gauss(tol/1))} | 68,2% (1σ) |
| {nom*(1+gauss(tol/2))} | 95,4% (2σ) |
| {nom*(1+gauss(tol/3))} | 99,7% (3σ) |
| {nom*(1+gauss(tol/4))} | 99,99% (4σ) |
Tabelle 3. Definition von Bauteilwerten und Toleranzen mit der Gaußschen Normalverteilungs-Methode. (Quelle: Analog Devices)
In grafischer Form sieht dies wie folgt aus:
Zum Erstellen eines 100-Ω-Widerstands mit einer Toleranz von ±10 % und einer 4σ betragenden Wahrscheinlichkeit, dass der Wert in den Toleranzbereich fällt, ist beispielsweise die folgende Syntax zu benutzen:
{100R*(1+gauss(ToIA/4))}
.param ToIA = 0.10
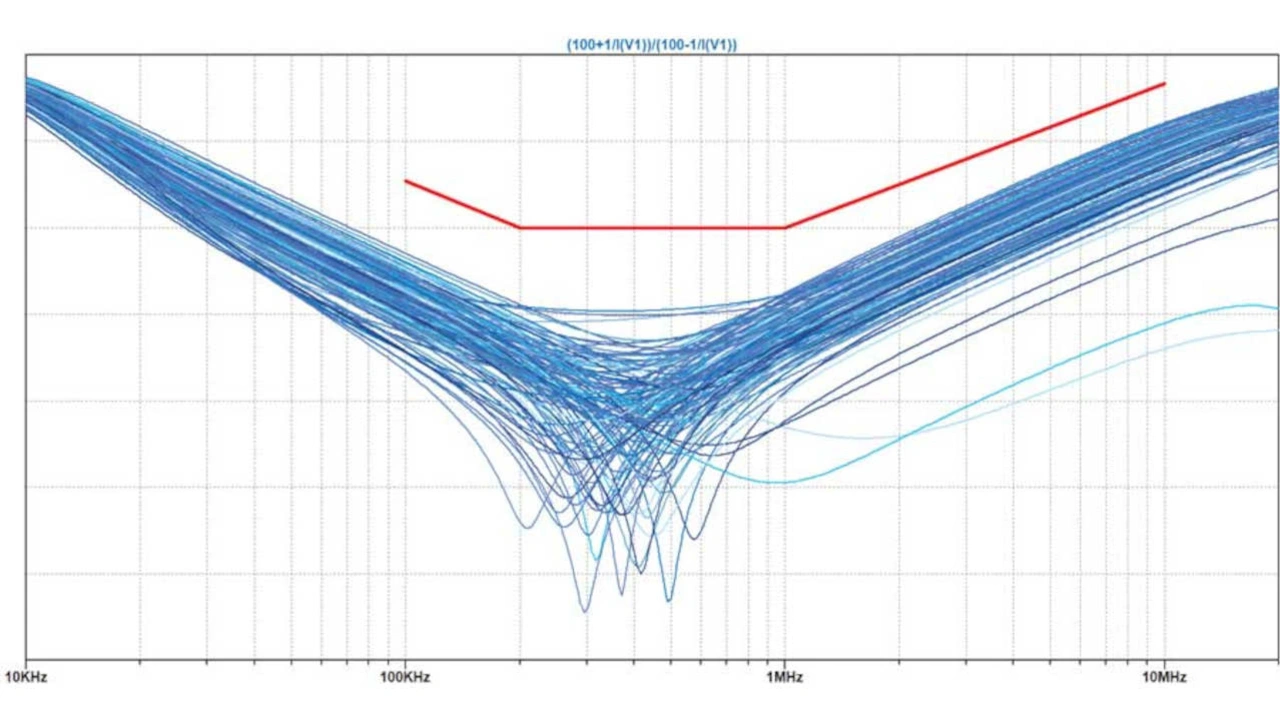
Bild 26 gibt die Ergebnisse von 128 Durchläufen der in Bild 19 gezeigten Simulation wieder, basierend auf einer Gaußschen Normalverteilung der Parameter mit 4σ.
Zusammenfassung der Gaußschen Simulation
Die Gaußsche Normalverteilung ist oftmals die sinnvollste Möglichkeit, die Variationen einer Elektronikschaltung zu simulieren, denn die Streuung der Parameter nach der Gaußschen Normalverteilung ist nach wie vor die folgerichtigste Art, die Auswirkungen von Toleranzen zu untersuchen. Dies hat jedoch seinen Preis, denn für eine wirklich gründliche Analyse sind sehr viele Simulationsdurchläufe erforderlich. Diese Verteilung schließt zudem auch Werte außerhalb des Toleranzbereichs ein und lässt damit den Sortierungs- und Binning-Prozess der Bauteilhersteller außen vor.
- Verbesserung der Signalintegrität
- Bewertung der Konformität über den Toleranzbereich
- Anwendung auf eine 10BASE-T1L-Verbindung
- Literatur
- Programme