Eigenschaften von Schwingquarzen
Siliziumoxid als Taktgeber
Fortsetzung des Artikels von Teil 2
Die Quarzschnitte im Einzelnen
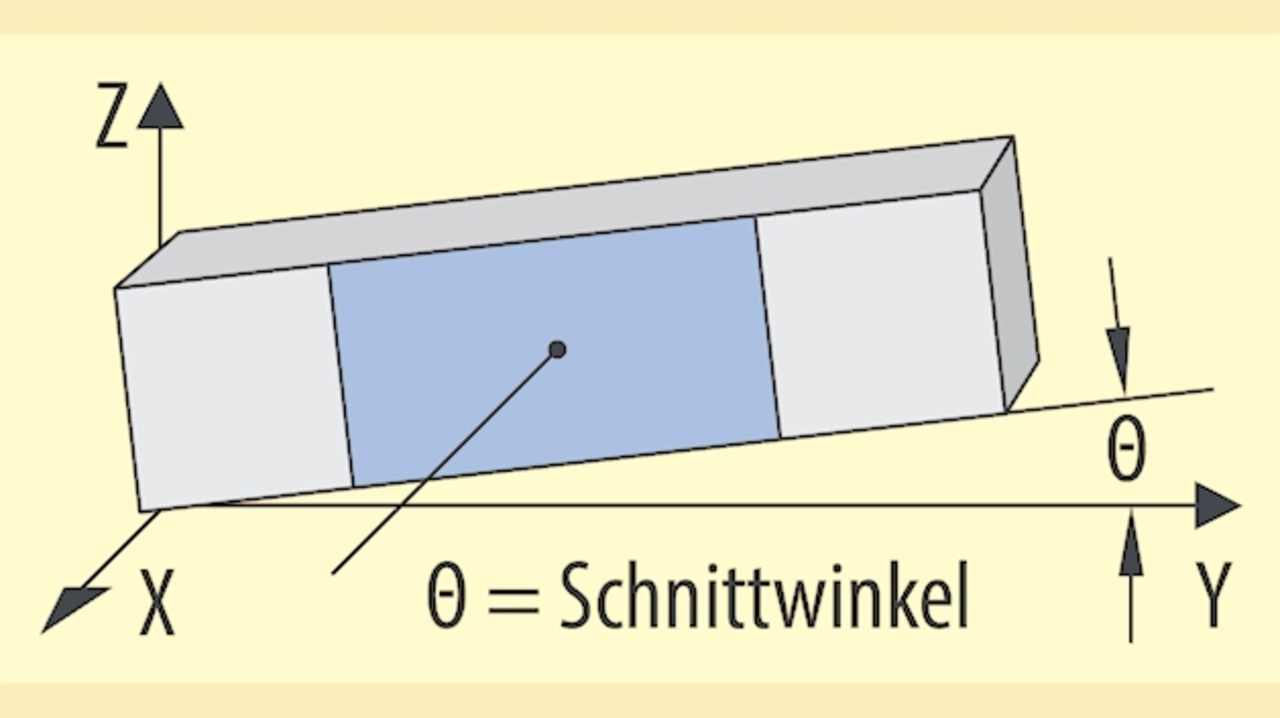
Zur Erzielung bestimmter Eigenschaften – meist eines minimalen Temperaturganges der Resonanzfrequenz und gleichzeitig einer guten elektrischen Anregbarkeit der gewünschten Schwingungsform über den Piezoeffekt – ergeben sich optimale Winkel (Schnittwinkel), unter denen die Schwingkörper (Resonatoren) aus dem Quarzkristall herausgeschnitten werden – siehe Bild 6.
Jobangebote+ passend zum Thema
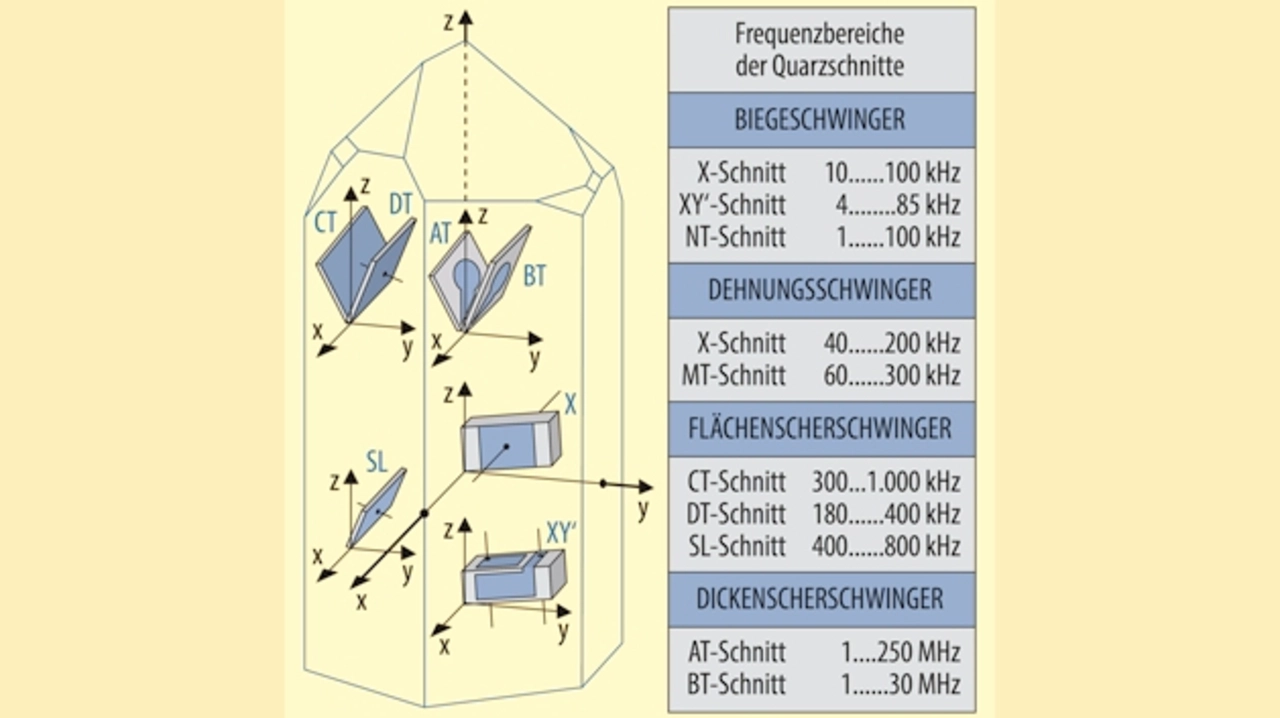
Die Bezeichnung der Schnitte entstand aus der alphabetischen Aufzählung der Schnittwinkel, die zu einem minimalen Temperaturkoeffizienten bei Raumtemperatur führten. Der Buchstabe „T“ steht für temperaturkompensiert. Eine andere Regel bezeichnet die Schnitte nach der kristallografischen Achse, die normal oder annähernd normal zur Hauptoberfläche des Schwingers steht. Es gibt noch Spezialschnitte, z.B. mit geringer Verkopplung zu anderen Schwingungsmoden (AC-Schnitt) oder mit besonders geringer Frequenzänderung bei mechanischen Beanspruchungen (SC-Schnitt = stress compensated).
Der Dehnungsschwinger
Dehnungsschwinger oder Longitudinalschwinger (Bild 7) sind plattenförmige Schwinger, die in Richtung ihrer längeren Abmessung (in Y-Richtung) schwingen, also durch das in X- Richtung angelegte elektrische Wechselfeld in Richtung der Y-Achse elongieren.
Zur Bestimmung der Eigenresonanz wird im Allgemeinen die Differenzialgleichung md2x/dt2 + cdx/dt + kx = 0 gelöst.
Anschaulicher betrachtet kann man hier von einer akustischen Welle ausgehen, die im Zentrum des Schwingers erzeugt wird. Diese Welle schreitet in ihrer Ausbreitungsrichtung mit der Schallgeschwindigkeit ν = √(1/(ρ·S) fort – im Fall der Längendehnung in Längsrichtung des Resonators. An den Enden des Resonators erfolgt eine Totalreflexion. Durch Überlagerung der hin- und rücklaufenden Welle entsteht im Resonanzfall eine stehende Welle, und zwar dann, wenn die Resonatorlänge ein ganzes Vielfaches der halben Wellenlänge ist.
Längendehnungsschwinger werden hauptsächlich für den Einsatz in Quarzfiltern hergestellt. Zudem werden Dehnungsschwinger aber auch als Mikroresonatoren in Hybrid-Schaltkreisen integriert.
Der Biegungsschwinger
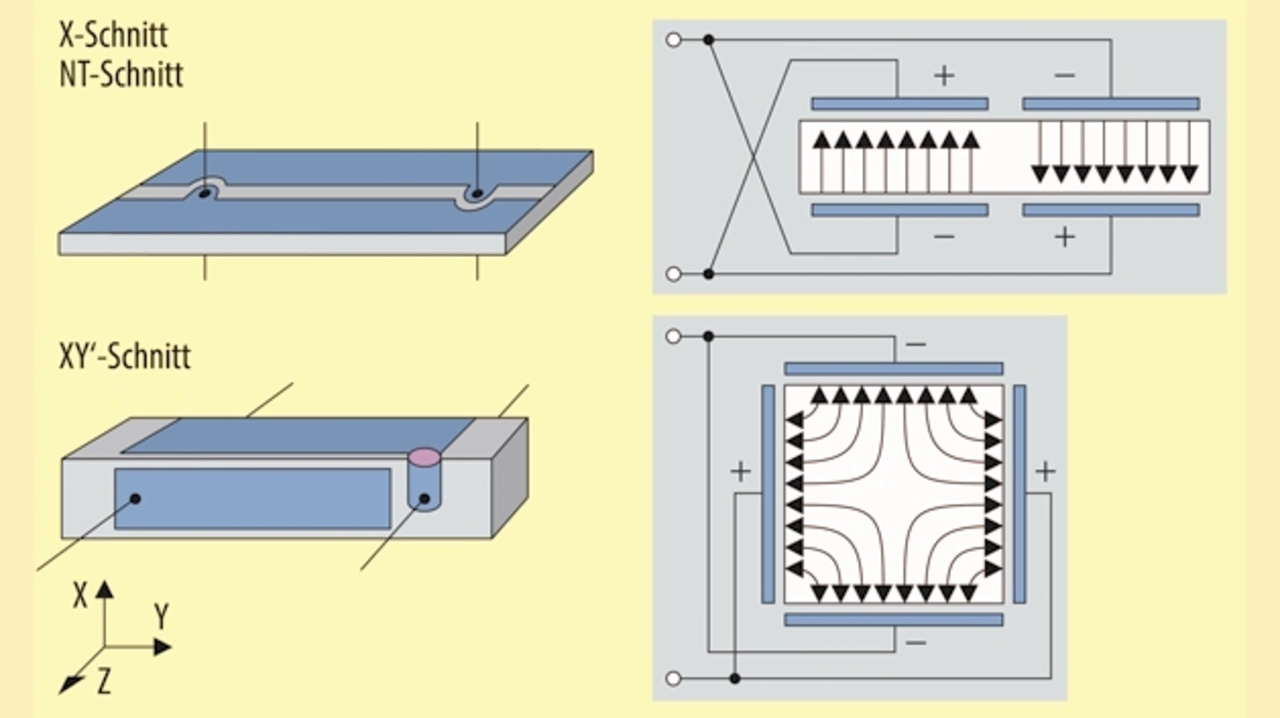
Biegungsschwingungen können erregt werden, indem X-Schnitt-Dehnungsschwinger (Bild 8) mit zwei gegenphasig angeschlossenen Elektroden versehen werden, so dass zwei entgegengesetzte Felder in X-Richtung auftreten. Die hierdurch erzwungene Biegung in Z-Richtung hat allerdings einen ungünstigen Temperaturgang der Resonanzfrequenz. Dieser Temperaturgang kann durch eine zusätzliche, zweite Drehung des Schnittes um die Y-Achse kompensiert werden (NT-Schnitt). Zu besseren Ergebnissen gelangt man mit dem allerdings hochohmigeren XY-Schnitt. Bei diesem Schnitt wird durch die Querfelderregung des quadratischen Stabes eine Biegung in X-Richtung mit den besseren Temperatureigenschaften erzwungen.
Stimmgabelquarze
Die bekannte Form der Stimmgabel mit Stiel stammt von dem englischen Gardetrompeter John Shore. In der Musik hat die Stimmgabel ihre große Bedeutung dank ihrer hohen Schwingungsgüte (Schwingungsdauer nach dem Anschlagen) und der guten Frequenzkonstanz.
Im einfachsten Fall wird die Gabel wie ein X-Schnitt-Biegeschwinger aus dem Kristall geschnitten. Es tritt damit auch der gleiche Nachteil auf – der des ungünstigen Temperaturganges der Frequenz. Durch geeignete Formgebung kann der Gabelstiel entkoppelt werden, sodass die Gabel am Fuß dämpfungsarm montiert werden kann.
Literatur
[1] Neubig, B.; Briese, W.: Das große Quarzkochbuch. Franzis-Verlag (ausverkauft)
[2] www.axtal.de/Deutsch/TechnInfo/Quarzkochbuch
- Siliziumoxid als Taktgeber
- Die kristallografischen Achsen
- Die Quarzschnitte im Einzelnen
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Coftech / Quarze & Oszillatoren
Taktgeber unserer digitalen Welt
Quarze und Oszillatoren
Kongress vermittelt Aktuelles zu Forschung und Anwendung
Oszillator für IoT-Funksensorknoten
Effizienter Schnellstart
Schukat
5.000 Quadratmeter mehr
Training for Professionals
Quarze und Oszillatoren – Aus der Praxis, für die Praxis
Quarze, Oszillatoren und Resonatoren
Frequenzgeber für jedes Anforderungsprofil
Quarzoszillatoren von Axtal
OCXO: Extrem rauscharme Variante
