Eigenschaften von Schwingquarzen
Siliziumoxid als Taktgeber
Fortsetzung des Artikels von Teil 1
Die kristallografischen Achsen
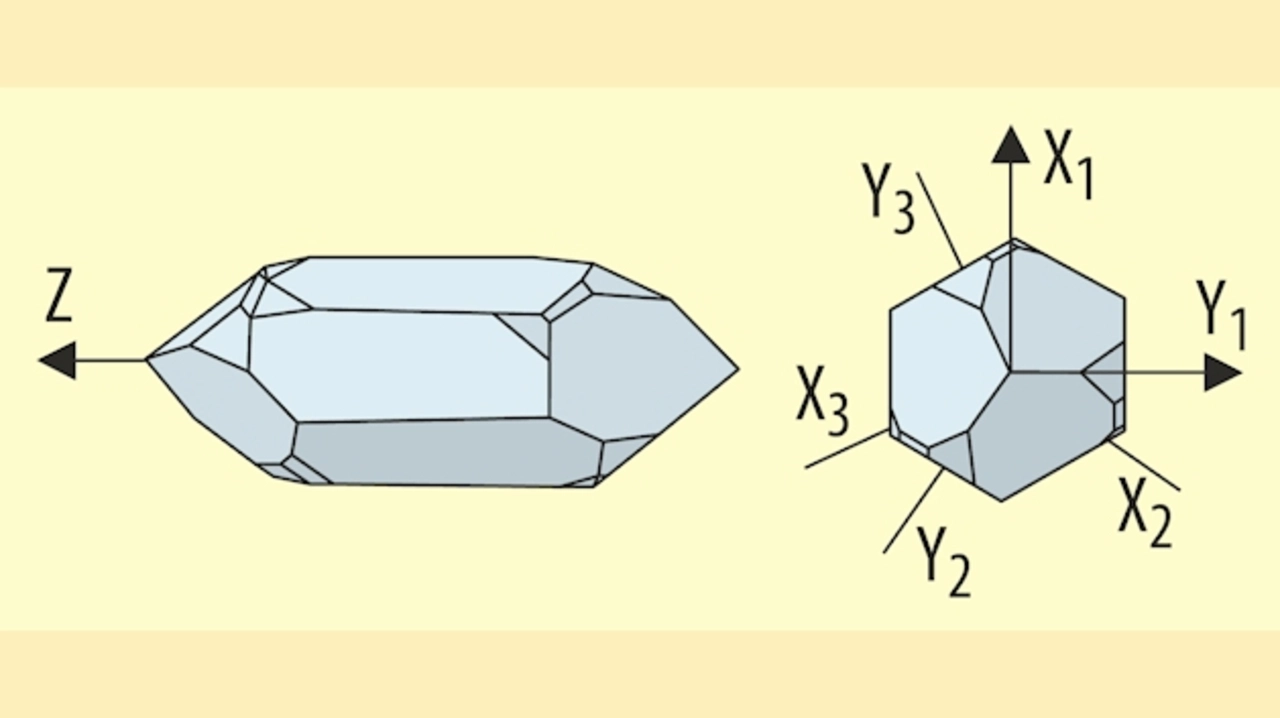
Ausgehend von der Gestalt eines natürlichen – im Querschnitt sechseckigen – Quarzkristalls und der in der Kristallografie üblichen Festlegung der senkrecht aufeinanderstehenden Koordinaten X, Y und Z lässt sich als Z-Achse die durch die Spitze des Kristalls gehende gedachte Achse (Bild 2) definieren. Die Z-Achse wird auch optische Achse genannt, weil in ihrer Richtung die optische Erscheinung der Doppelbrechung zu beobachten ist. Die senkrecht hierzu stehende und durch eine Ecke des hexagonalen Prismas gehende X-Achse wird auch elektrische Achse genannt, weil durch Deformation des Kristalls in dieser Richtung eine elektrische Ladung auftritt (direkter Piezoeffekt). Die Y-Achse steht senkrecht zu den beiden anderen Achsen und geht damit durch eine Fläche des Kristalls (Bild 3).
Jobangebote+ passend zum Thema
Bei Anlegen einer elektrischen Ladung in Richtung der X-Achse tritt eine Elongation in Richtung der Y-Achse auf (indirekter Piezoeffekt). Die Y-Achse wird auch die mechanische Achse genannt.
Der piezoelektrische Effekt
Das Wort Piezo stammt aus dem griechischen „pizein“. Es bedeutet drücken oder pressen. Piezoelektrisch heißt also elektrische Ladung durch mechanischen Druck. Durch mechanische Deformation bestimmter Kristalle entsteht auf deren Oberflächen eine elektrische Ladung. Diese Erscheinung nennt man den direkten piezoelektrischen Effekt. Umgekehrt nennt man die Entstehung einer Deformation des Kristalles aufgrund einer elektrischen Ladung den umgekehrten piezoelektrischen Effekt. Beide Effekte sind streng proportional. Voraussetzung für die piezoelektrische Eigenschaft eines Kristalls ist das Vorhandensein einer polaren Achse.
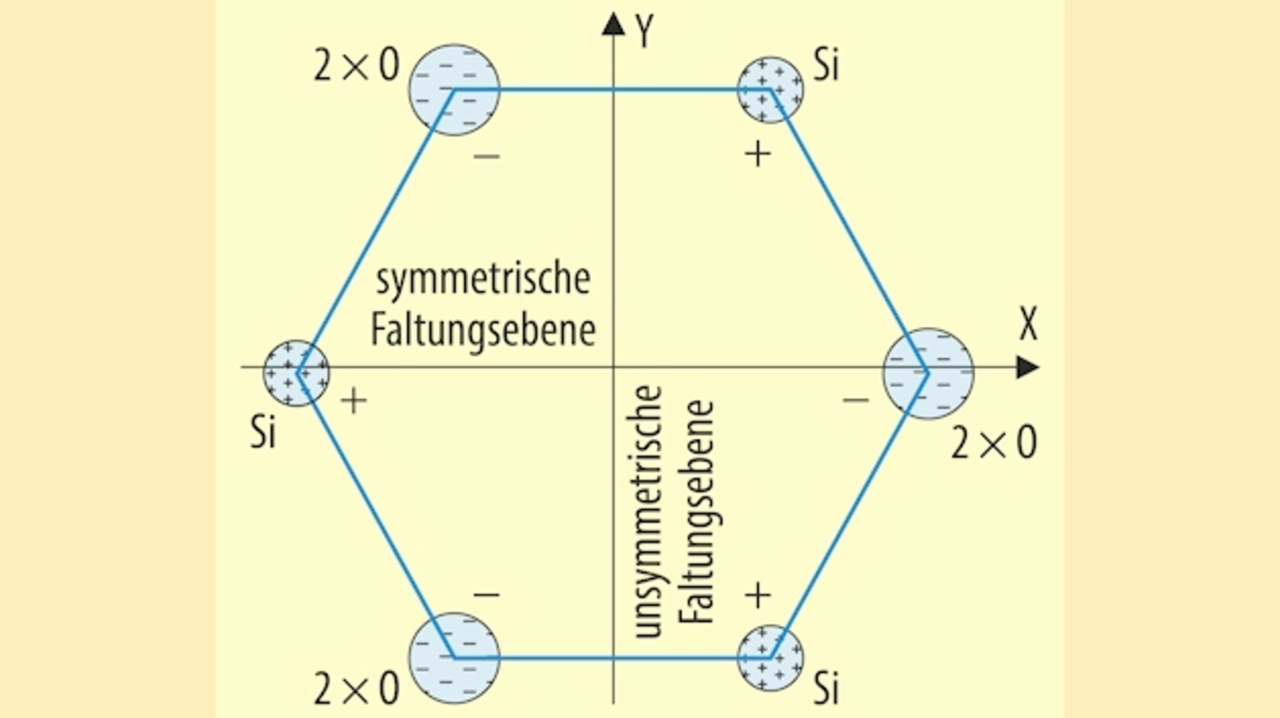
In der Kristallografie nennt man eine Kristallachse polar, wenn bei Drehung um diese Achse die Strukturzelle nicht deckungsgleich ist. Man spricht auch von einer unsymmetrischen Faltungsebene. Beim Quarz ist die X-Achse die polare Achse. In Bild 3 ist die Strukturzelle von Quarz vereinfacht dargestellt. Die kleinen Kreise stellen hierbei die positiv geladenen Si-Ionen dar, die größeren Kreise die negativ geladenen O-Ionen des SiO2-Kristallgitters. Verformt man den Kristall durch Druck in Richtung der X-Achse, verschieben sich die positiven und negativen Ionen gegeneinander. Es entsteht eine elektrische Polarisation in Richtung der X-Achse. Die Folge ist eine elektrische Ladung auf den entsprechenden Oberflächen des Kristalls – in diesem Fall auf den X-Flächen.
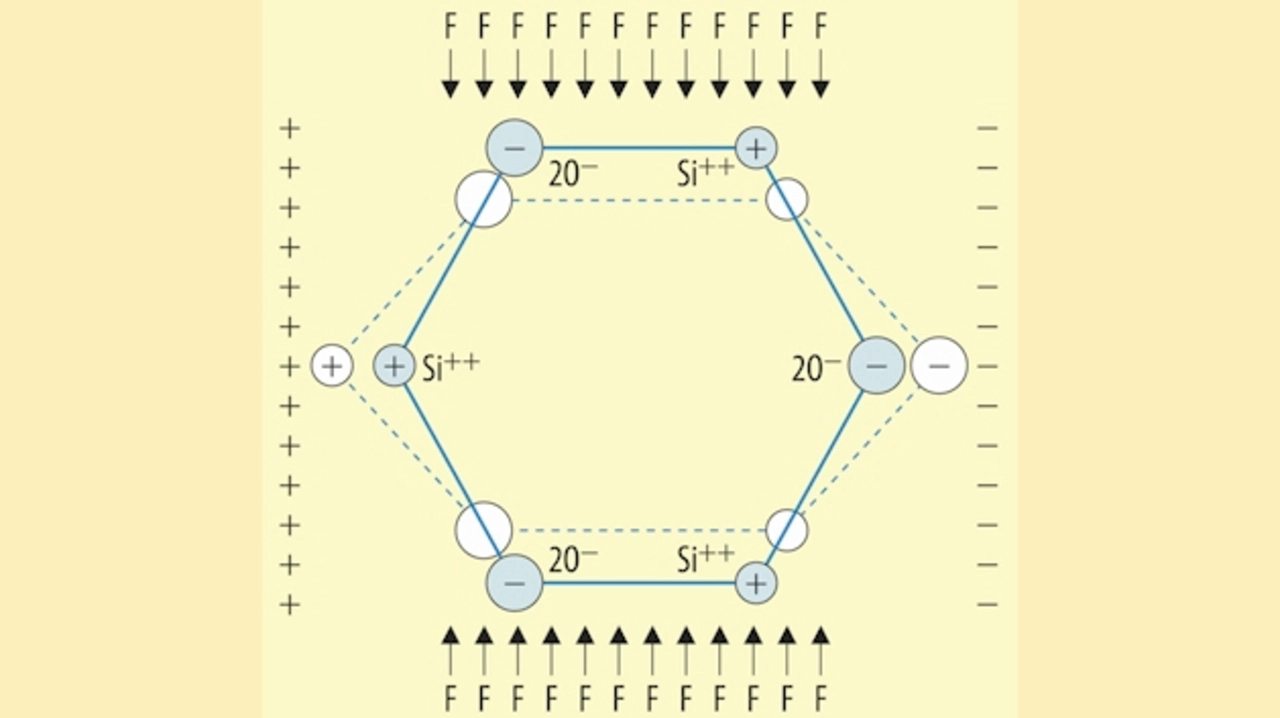
In Richtung der Y-Achse kann keine Polarisation erfolgen, weil diese Achse eine symmetrische Faltungsebene darstellt. Bei Druck- oder Zugbeanspruchung in Richtung der Y-Achse („F“ in Bild 4) entsteht jedoch ebenfalls in X-Richtung eine Polarisation. Dieser Vorgang wird der transversale Piezoeffekt genannt. Die Y-Achse wird dementsprechend auch die mechanische Achse genannt. Die geschilderten piezoelektrischen Wirkungen sind reversibel. Das heißt, unter Einwirkung eines elektrischen Feldes in Richtung der X-Achse deformiert sich der Kristall in Richtung der Y-Achse. Man nennt dies auch den indirekten Piezoeffekt.
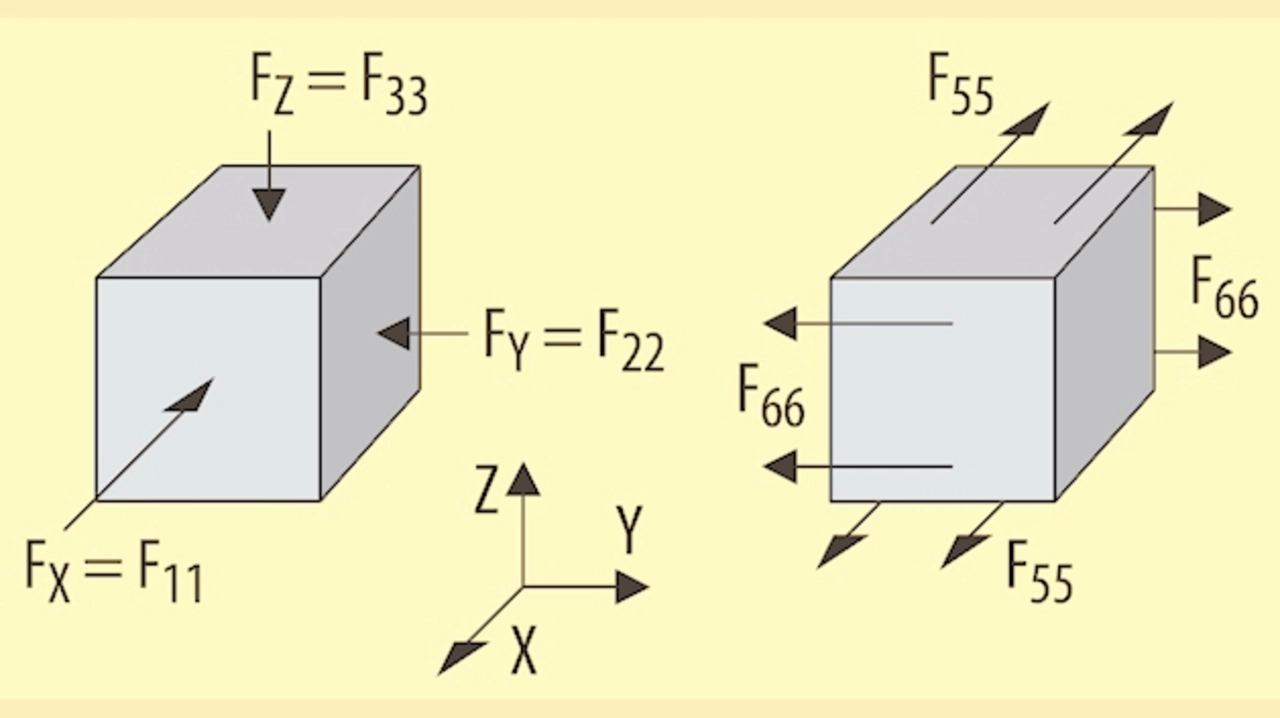
Bedingt durch seine Kristallstruktur gibt es beim Quarzkristall drei völlig gleichwertige X-Achsen, die unter einem Winkel von 120° zueinander stehen. Zu jeder X-Achse gehört jeweils eine Y-Achse (Bild 2). Die Werte der piezoelektrischen und mechanischen Parameter sind von der Richtung ihrer Wirkung in Bezug auf die Kristallachsen abhängig. Die richtungsabhängigen Komponenten werden deshalb sinngemäß indiziert, entweder mit der Bezeichnung der Achse oder bei den Druckkomponenten durch Zählung 1, 2, 3 für die Richtungen X, Y, Z. Die Zählung der Scherkomponenten (Schubspannungen) erfolgt entsprechend mit den Indizes 4, 5, 6. Flächen werden mit der Bezeichnung der Achse indiziert, die senkrecht zu der betreffenden Fläche steht (Bild 5).
Vorausgesetzt, dass in gleicher oder in anderer Richtung keine weiteren Kräfte herrschen, lässt sich für den longitudinalen direkten Piezoeffekt folgende mathematische Gleichung erstellen:
Qx = d11 · Fx = d11 · F11
- Siliziumoxid als Taktgeber
- Die kristallografischen Achsen
- Die Quarzschnitte im Einzelnen