Passive Sensoren
Drahtlos versorgt und abgefragt
Fortsetzung des Artikels von Teil 1
Dimensionierung der induktiven Kopplung
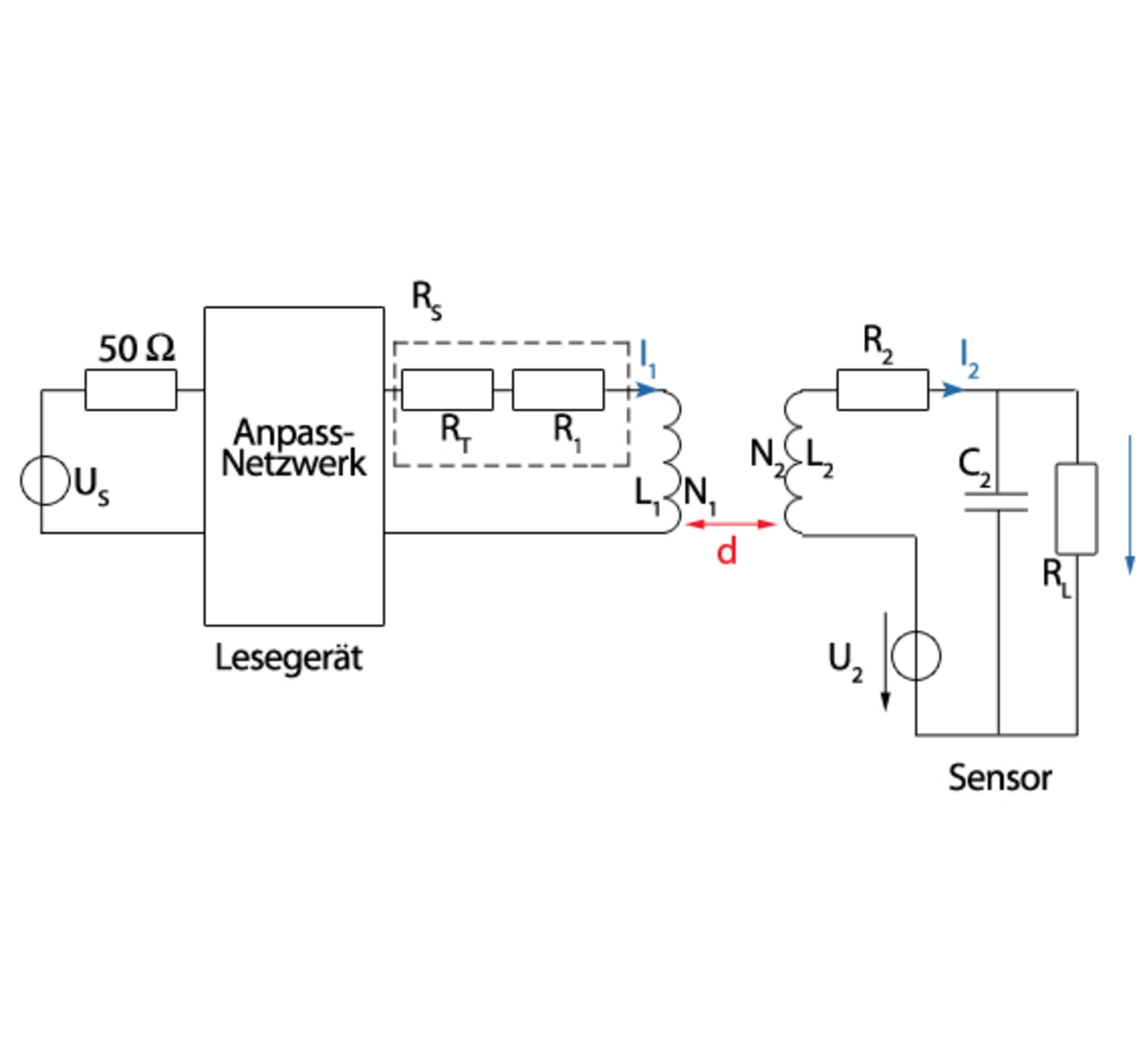
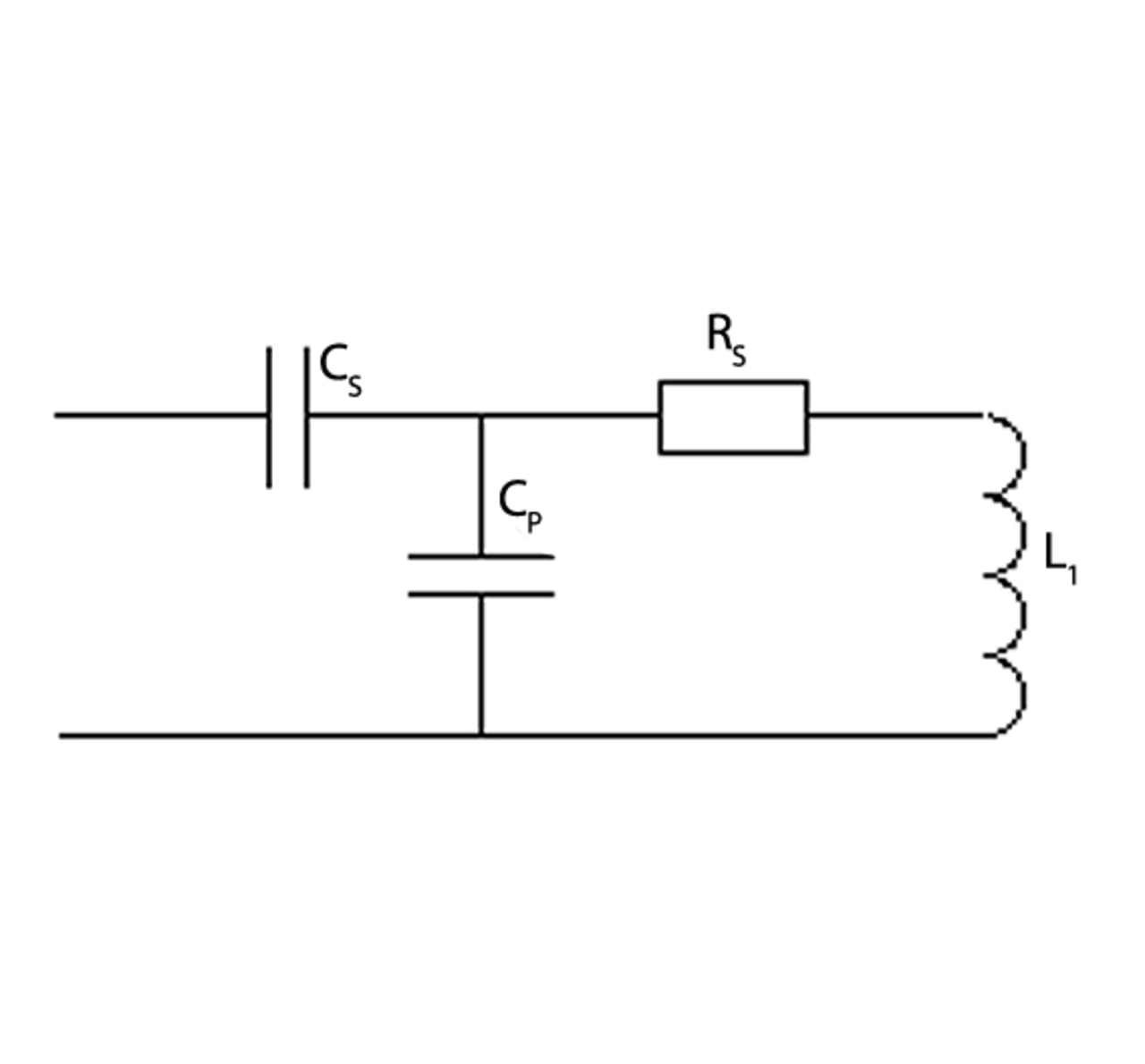
Die grösste Schwierigkeit beim Systementwurf bereitet die effiziente Leistungskopplung über eine vorgegebene Distanz. Der Kopplungskoeffizient beträgt für größere Spaltbreiten zwischen den beiden Systemteilen schnell nur noch wenige Prozent [Fink]. Daran lässt sich leider bei gegebener Geometrie nichts ändern. Einzig bei der Senderstufe kann auf einen hohen Wirkungsgrad hingearbeitet werden und ein Klasse-E-Verstärker eingesetzt werden. Aus der Erfahrung mit Transformern erwartet man eine stattliche Anzahl Windungen als Optimum, um genügend Spannung auf der Sekundärseite zu erzeugen. Induktive Kopplungen bei HF werden aber ganz anders ausgelegt. Man bedient sich der Technik der Resonanzkreise. Die Versorgungsquelle US (Klasse E Endstufe) in Bild 2 besitzt einen Ausgangswiderstand von 50 Ω. Die primäre Spule (Induktivität L1) mit N1 Windungen und Verlustwiderstand R1 (f(Querschnitt, Länge, Skintiefe)) wird mit Hilfe eines Anpassnetzwerkes bei der Resonanzfrequenz 13,56 MHz auf 50 Ω angepasst.
Im Sensor wird die Empfangsspule (Induktivität L2) mit C2 in Parallelresonanz abgestimmt. Es zeigt sich, dass dann die Spannung UL über der Last dem Produkt der induzierten Spannung U2 mal der Schwingkreisgüte Q2 entspricht. Die induzierte Spannung durch das Magnetfeld H(x) und die Gegeninduktivität M(x) sind proportional zu N2.Es gelten folgende Beziehungen:
(1) 
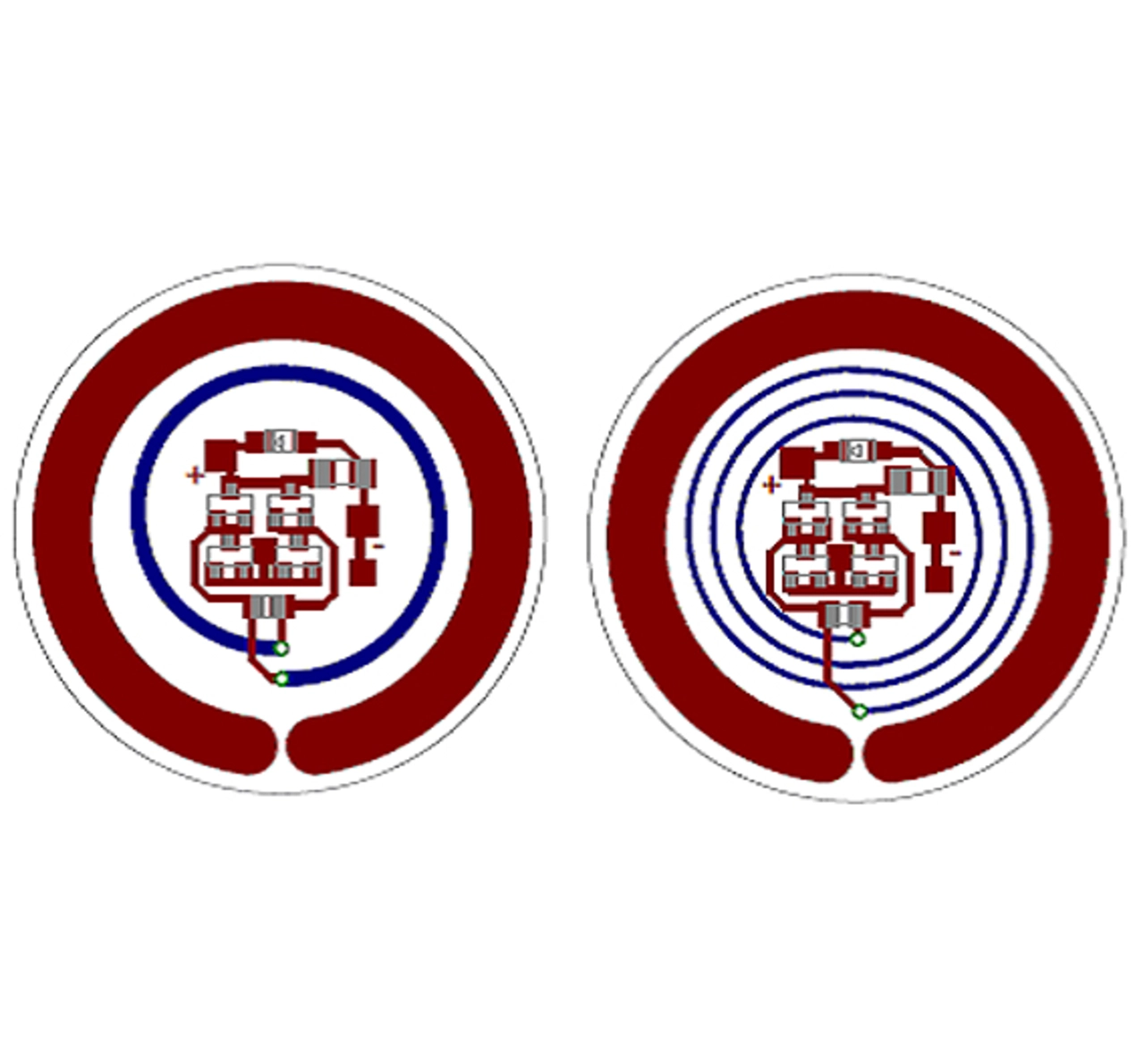
In (1) entspricht A2 der Fläche der Spule L2 und N2 deren Windungszahl. Um die Übersicht zu wahren gehe man im Folgenden von einer vorgegeben Baugröße für die Applikation aus (Bild 3, Radius 10 mm), so dass UL nur durch N2 und Q2 beeinflussbar ist. R2 stellt die Verluste der Induktivität L2 dar welche ungefähr proportional zu N2 sind.
Wie soll nun L2 dimensioniert werden, wie viele Windungen sollen es sein?
Die Antwort ist viel Schwieriger als man denkt.
RL ist durch den Verbraucher gegeben, ebenso C2 für die Erzeugung der Resonanz sobald L2 einmal fixiert ist. Es treten gewissermaßen 2 Güteanteile im Sensorkreis auf: Einer aus L2 und R2 in Serie (QR2 ) und einer aus L2 und RL parallel (QRL).
Es gilt ungefähr (siehe auch Kasten Serie-Parallel-Wandlung im Schwingkreis):
(2) 
Möchte man den unnützen Verlust in R2 minimieren und Q2 groß werden lassen, so dass UL in (1) groß wird, dann muss interessanterweise neben R2 auch L2 klein gemacht werden. Andrerseits soll die Gegeninduktivität M(x) welche proportional zur Windungszahl N2 ist groß sein um U2 groß zu machen.
Für niederohmige Lasten wird die Güte hauptsächlich durch RL bestimmt:
(3) 
Da L2 proportional zum Quadrat von N2 ist, dominiert Q2 den Einfluss von M(x). Für niederohmige Lasten RL soll also N2 minimal werden, d.h. theoretisch nur eine einzige Windung betragen. In der Praxis ist aber R2 nicht beliebig klein realisierbar und beginnt nach (2) auf Q2 Einfluss zu nehmen, insbesondere wenn L2 sehr klein wird. Für eine Einzelwindung mit Radius 10 mm werden gerade noch 
40 nH gemessen mit einem Q2 von 30. Es ist dann bei kleinen Geometrien N2 = 2 oder 3 oft die optimalere Lösung.
Wird die Koppelstrecke in Metall eingebettet, so ist auch mit den Wirbelstromverlusten zu rechnen. In diesem Fall steigt R2 unabhängig von L2. L2 muss nun für ein ansprechendes Q2 ebenfalls erhöht werden.
Man kann auch theoretisch zeigen [Theodoridis], dass N2 dem aufgerundeten Wert von (4) entsprechen soll um maximale Spannung an RL zu erhalten:
(4) 
Hierbei sind für R20 und L20 die Ersatzwerte für eine Einzelwindung der geplanten Spulenbaugröße einzusetzen. Im Größebeispiel nach Bild 3 misst man: L20 
40 nH, R20 0.14 Ω. Für RL = 300 Ω ergibt sich N2 = 2. Dies scheint im Einklang mit obigen Überlegungen.
Könnte man nun einfach mit einer kleineren Baugröße etwas verbessern?
Nein, denn die Abnahme von R20 und L20 (hier beide proportional zum Spulenradius (siehe Tabelle Abhängigkeiten, Seite 3)) wird mehr als kompensiert durch die verringerte Gegeninduktivität M(x). Diese nimmt proportional zur Spulenfläche A2 ab. Nur eine größere und damit oft unpraktische Baugröße würde die Reichweite verbessern.
Für RFID-Etiketten liegt übrigens RL im Bereich von 10 kΩ und mehr, so dass bei Kreditkartengröße N2 typisch 4 bis 6 wird.
- Drahtlos versorgt und abgefragt
- Dimensionierung der induktiven Kopplung
- Dimensionierung der induktiven Kopplung - Teil 2
- Design Klasse-E-Verstärker
Lesen Sie mehr zum Thema
