»ERES« und »HiRes«
Hohe Auflösung - aber wie?
Fortsetzung des Artikels von Teil 2
Entscheidend: Es wird immer interpoliert
Tabelle 2a zeigt die Bandbreitenbegrenzung einer HiRes-Erfassung in Abhängigkeit der Filterlänge. Diese Tabelle ist auf der Tektronix-Internetseite zu finden.
Jobangebote+ passend zum Thema
| Abtastrate |
Auflösung | 3-dB-Bandbreitenlimit (0,44 × Abtastrate) |
|---|---|---|
| 2,5 GS/s |
8,5 bit |
1,1 GHz* |
| 1 GS/s |
9 bit |
440 MHz |
| 250 MS/s |
10 bit |
110 MHz |
| 50 MS/s |
11 bit |
22 MHz |
| 10 MS/s |
12 bit |
4,4 MHz |
| 2,5 MS/s |
13 bit |
1,1 MHz |
| 1 MS/s |
14 bit |
440 kHz |
| 250 kS/s |
15 bit |
110 kHz |
| 25 kS/s |
>15 bit |
11 kHz |
| 250 S/s |
>15 bit |
110 Hz |
| 25 S/s |
>15 bit |
11 Hz |
| 2,5 S7s |
>15 bit |
1,1 Hz |
| **Dies ist die Filterbandbreite. Die Bandbreite des Oszilloskops entspricht der analogen Bandbreite des Eingangsverstärkers und ist hier 1 GHz. |
||
Tabelle 2a. Zusammenhang zwischen Abtastrate, Auflösung und Bandbreite beim HiRes-Modus.
Tabelle 2b stellt die in Tabelle 2a gegebenen Informationen in einer Art und Weise dar, dass diese einfacher mit Tabelle 1 zu vergleichen ist. Die Unterschiede in der Bandbreitenbegrenzung für verschiedene Filterlängen und zusätzliche vertikale Auflösung (Bits) sind dabei gut zu erkennen. Die in Tabelle 2a zu sehenden HiRes-Beispiele sind mit einem 8-Bit-Oszilloskop mit 5 GS/s gemessen.
| Erhöhung d. Auflösung [bit] | 3-dB-Bandbreite [GHz] | 3-dB-Bandbreite [× Nyquistfr.] | Filterlänge [Samples] |
|---|---|---|---|
| 0,5 |
1,0 |
0,4 |
2 |
| 1 |
0,44 |
0,176 |
5 |
| 2 |
0,11 |
0,044 |
20 |
| 3 |
0,022 |
0,0088 | 100 |
Tabelle 2b. Verringerung der Bandbreite bei Verwendung eines HiRes-Filters bei einem Oszilloskop mit einer Abtastrate von 5 GS/s (Nyquistfrequenz: 2,5 GHz).
Es gibt noch einen weit wichtigeren Effekt, den der Anwender bei der Verwendung des HiRes-Modus beachten sollte. Alle Oszilloskope schätzen den Signalverlauf zwischen zwei im Speicher erfassten Werten (entweder A/D-Wandler-Werte oder gefilterte/verarbeitete Werte) mit Hilfe eines Interpolations-Algorithmus, um auf dem Bildschirm eine durchgehende Signalform anzeigen zu können. Sowohl LeCroy wie auch Tektronix-Oszilloskope ermöglichen es dem Benutzer, zwischen einer linearen oder Sinus(x)/x-Interpolation zu wählen. In LeCroy-Oszilloskopen ist die lineare Methode als Standard eingestellt, während es bei Tektronix die Sinus-x/x Interpolation ist.
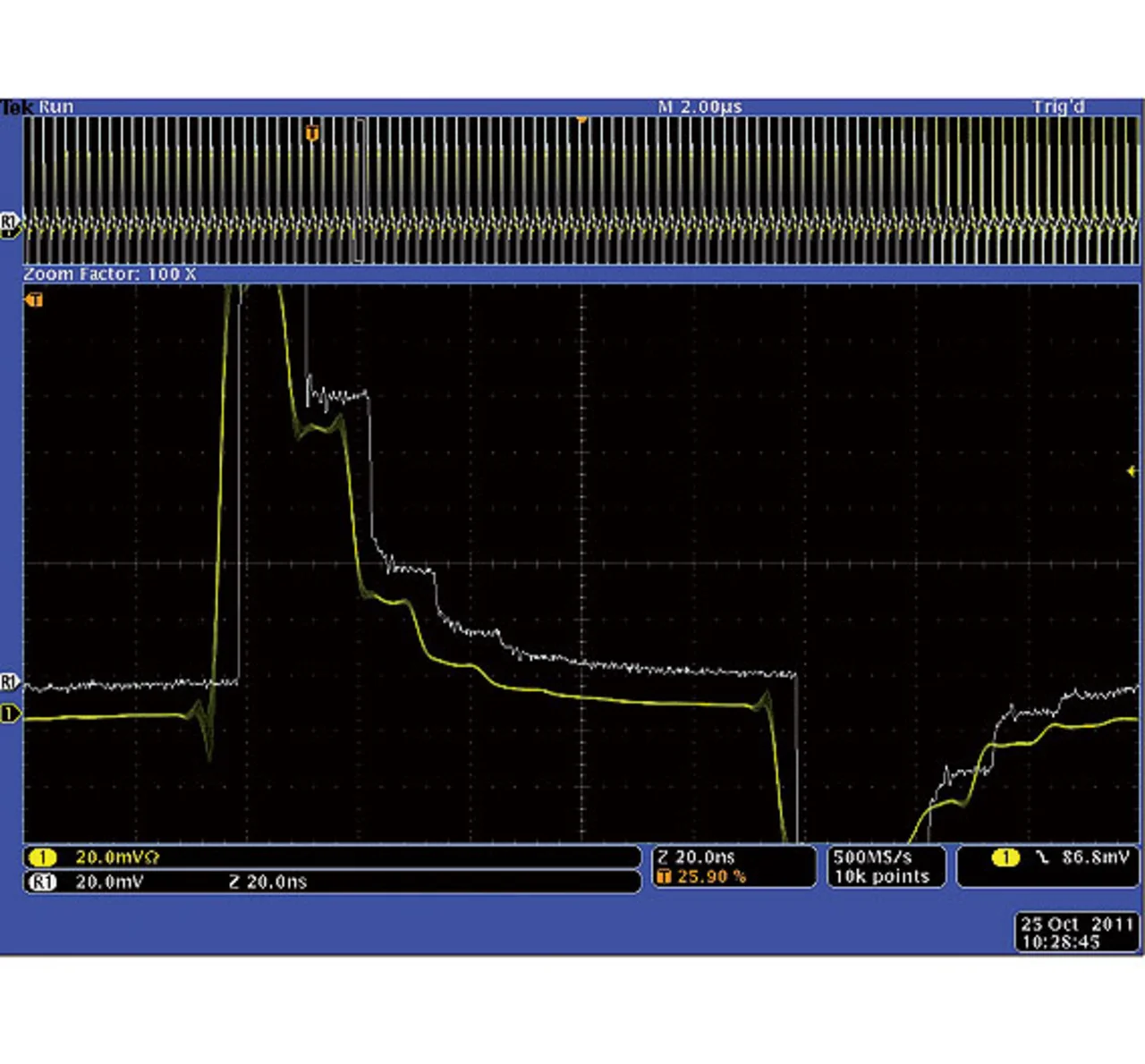
Ein mathematischer Effekt namens „Gibb Ears“ tritt dann auf, wenn auf eine unterabgetastete Flanke zur Interpolation zwischen den Erfassungspunkten die Sinus(x)/x-Methode angewendet wird. Das Oszilloskop fügt bei diesem Effekt im Vergleich zum realen Signal Vor- bzw. Überschwinger in das angezeigte Signal ein.
In der weißen Kurve in Bild 4 ist ein Signal zu sehen, das mit 5 GS/s, also der maximalen Abtastrate ohne den Einsatz von HiRes, erfasst wird. Das gelbe Signal hingegen ist das gleiche Signal wie das weiße, nur dass sich der Anwender hier mit der HiRes-Methode für eine erhöhte vertikale Auflösung entschieden hat, indem er durch eine Anpassung der Speichertiefe die Abtastrate auf 500 MS/s eingestellt hat. Zu beachten sind hier die Vor- bzw. Überschwinger im angezeigten Signal vor jeder Flanke.
Man könnte nun denken, dass reelle Überschwinger im Signal vorhanden sind, obwohl der tatsächliche Signalverlauf eigentlich optimal ist. Die Überschwinger kommen eben durch den mathematischen Effekt zustande, den die Sinus(x)/x-Interpolation auf unterabgetastete Signale mit sich bringt.
Wenn eine Flanke mit 10 Abtastpunkten erfasst wird, ist der Kurvenverlauf sehr präzise beschrieben, auch wenn eine Sinus(x)/x-Interpolation durchgeführt wird. Wenn aber zusätzlich eine Filtermethode wie “Box Car” angewendet wird und damit die zehn Erfassungspunkte z.B. um den Faktor 10 reduziert werden, ist plötzlich eine unterabgetastete Flanke vorhanden, die unweigerlich zu dem „Gibbs Ears“-Effekt führt. Generell kann gesagt werden, dass es dann mit der Sinus (x)/x-Interpolation zum „Gibbs Ears“-Effekt kommt, wenn eine Flanke weniger als zwei Abtastpunkte besitzt.
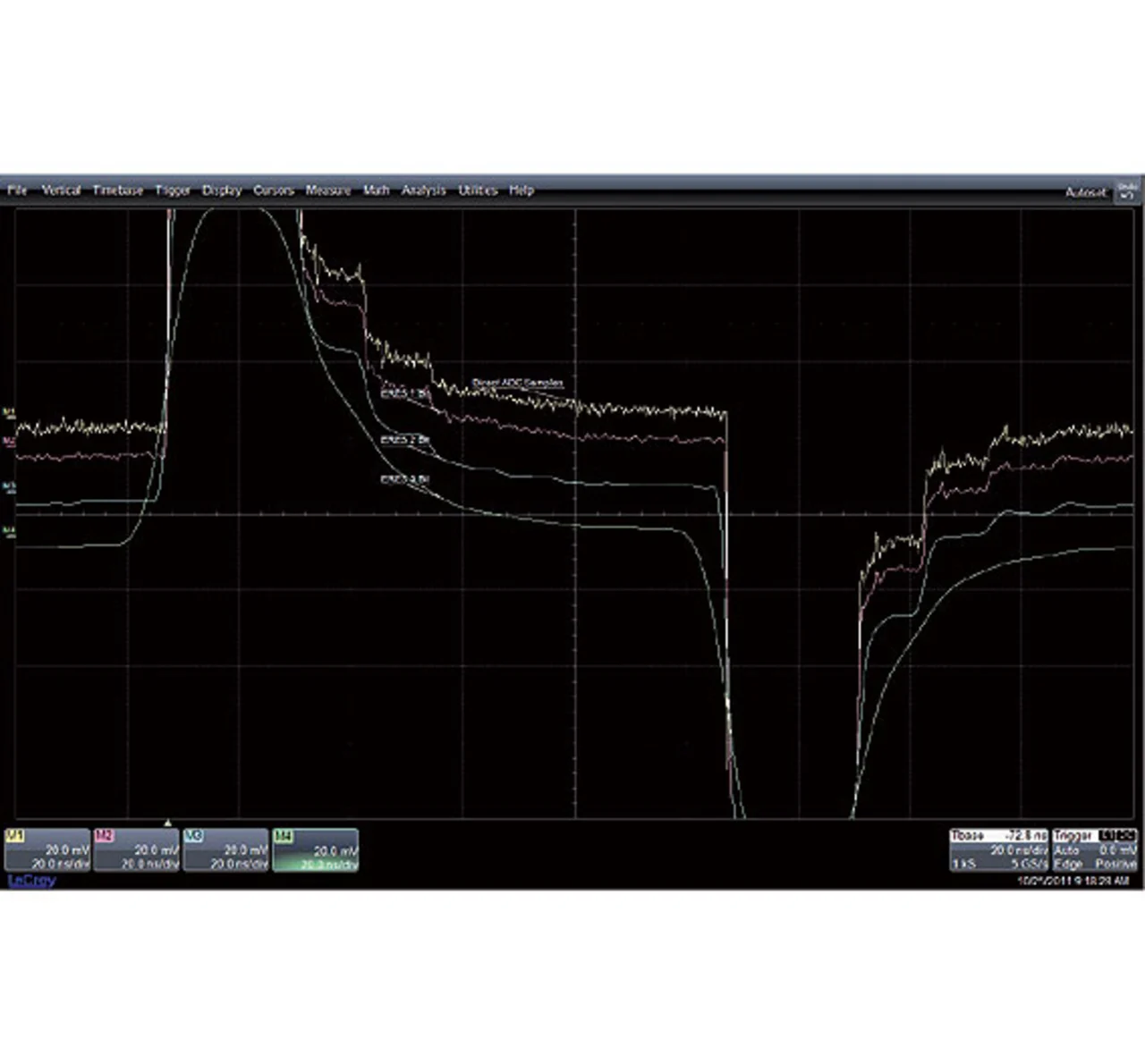
Im Gegensatz dazu wird bei der ERES-Methode jeder Erfassungspunkt durch einen neu berechneten Punkt ersetzt. So kommt es hier lediglich zu einer minimalen Reduzierung der Abtastpunkte um die Länge des eingestellten Filters. Jeweils die halbe Filterlänge wird am Anfang und am Ende der Erfassung abgeschnitten.
In Bild 5 sind neben dem originalen Signal noch drei mit ERES gefilterte Signale (mit unterschiedlicher Filterlänge) dargestellt. Die durch den Filter eingebrachten zusätzlichen Bits (1, 2 und 3 Bit) an Auflösung entsprechen einer Filterlänge von 5, 25 und 106 Punkten. Bei keiner der gefilterten Signale ist der „Gibbs Ears“-Effekt zu sehen.
- Hohe Auflösung - aber wie?
- Wie funktioniert HiRes?
- Entscheidend: Es wird immer interpoliert
- Erweiterte Anwendungen der Signalfilterung