»ERES« und »HiRes«
Hohe Auflösung - aber wie?
Um eine höhere Amplitudenauflösung der dargestellten Signale zu erzielen, verwenden moderne Oszilloskope spezielle Filter-Mathematik-Algorithmen. Hier ein vergleichender Blick auf zwei im Markt eingeführte Verfahren.
Sowohl die “ERES“- (Enhanced Resolution) Mathematikfunktion von LeCroy wie auch der “HiRes“- (High Resolution) Erfassungsmodus von Tektronix sind FIR-Filter (Finite Impulse Response). Ihre Funktion besteht darin, hochfrequente Anteile der Signale sowie hochfrequente Anteile von Rauschen aus dem Signal zu entfernen.
Abgesehen von dieser grundlegenden Ähnlichkeit der beiden Verfahren sind diese völlig unterschiedlich sowohl auf mathematischer als auch auf operativer Ebene.
Wie funktioniert ERES?
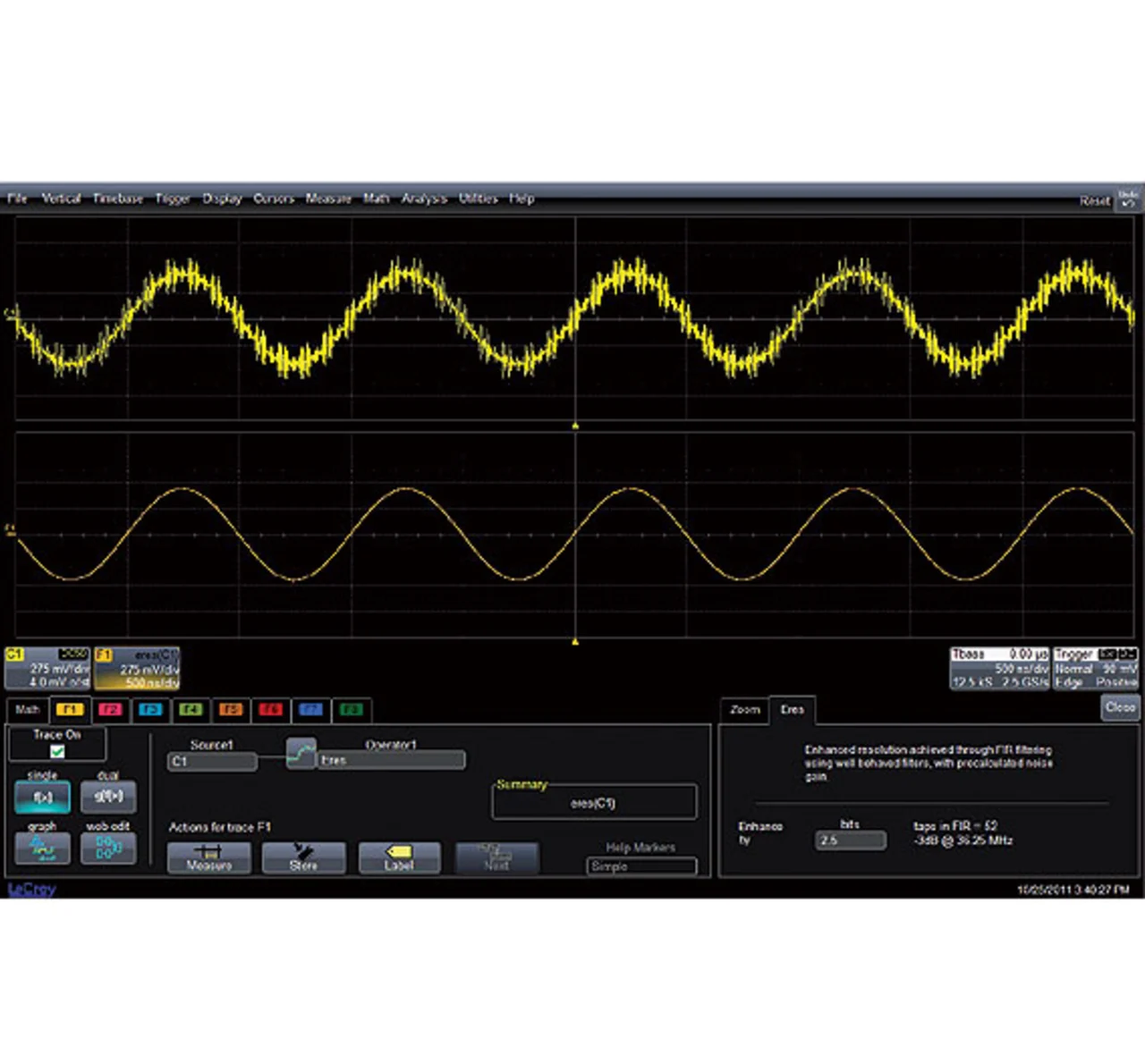
ERES ist eine „Post-Acquisition“-Funktion, die in vielen LeCroy-Oszilloskopen verfügbar ist. Der Anwender kann dabei die Stärke der Filterung in mehreren Stufen einstellen. In dem Beispiel in Bild 1a und 1b ist links unten im Dialogfeld ersichtlich, dass der Anwender eine Filterung eingestellt hat, die eine zusätzliche vertikale Auflösung von 2,5 Bits bietet. Die Einstellmöglichkeit für den Anwender sind 0,5 bis 3 Bits mehr Auflösung.
Jobangebote+ passend zum Thema
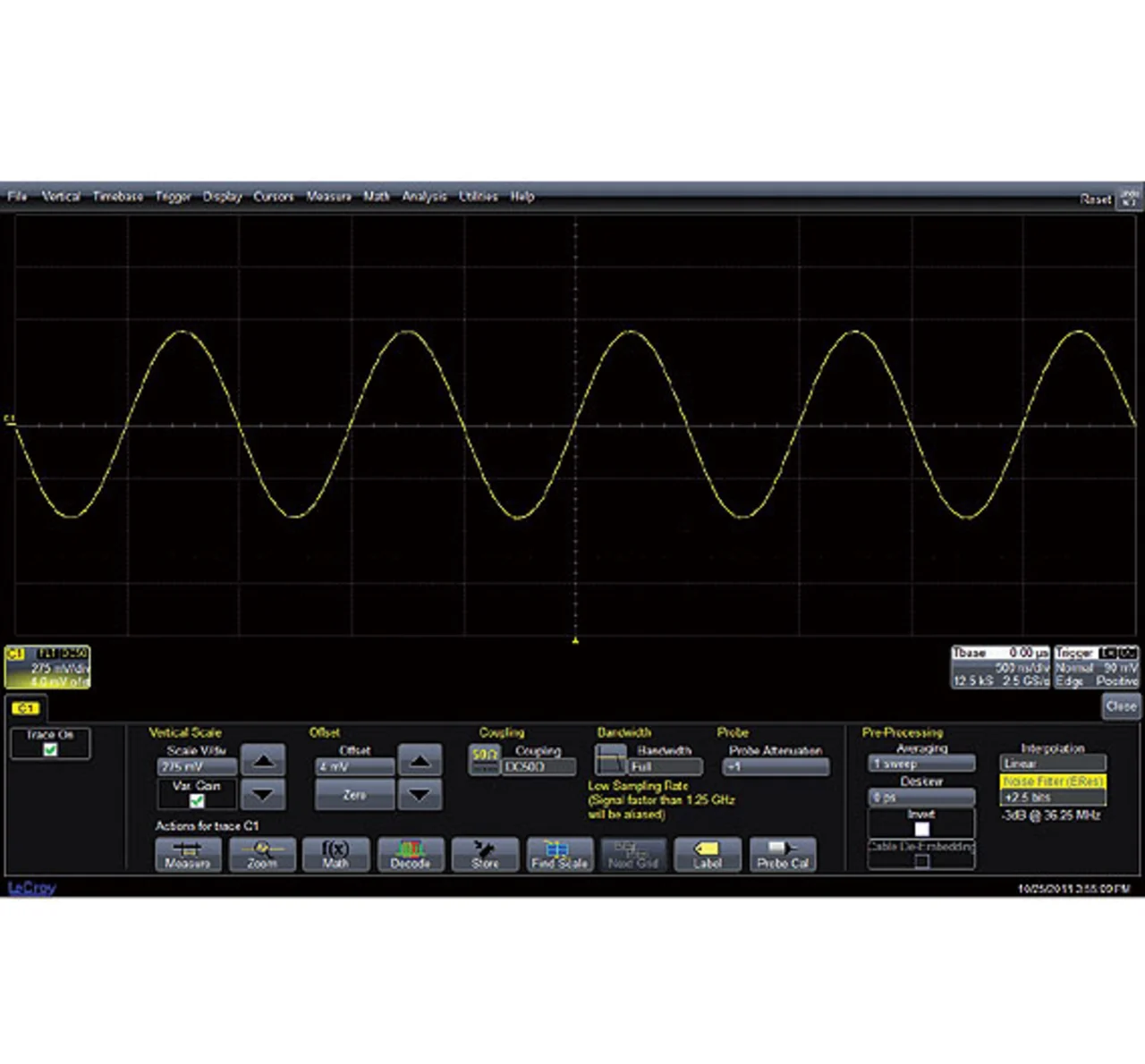
Natürlich hat der Gewinn von zusätzlicher Auflösung einen Nachteil an anderer Stelle. Der Nachteil ist im Dialogfeld ersichtlich. ERES filtert das Signal so, dass die Bandbreite des Signals kleiner ist als die Bandbreite der eigentlichen Erfassung. Das Dialogfeld zeigt eine 3-dB-Bandbreite von 36,25 MHz. Dies ist 0,029-mal die Bandbreite der ursprünglichen Erfassung.
Die ursprüngliche Erfassung wurde mit 2,5 GS/s durchgeführt (ersichtlich im Zeitbasis-Feld im unteren rechten Eck in Bild 1a), wofür das Nyquist-Theorem besagt, dass das Oszillokop Signale bis 1,25 GHz erfassen kann. Die Filterung durch die ERES-Funktion reduziert nun diese Bandbreite zugunsten einer besseren vertikalen Auflösung. Kürzere ERES-Filter reduzieren die Bandbreite geringer, ermöglichen aber auch nur eine geringere Biterhöhung.
Tabelle 1 zeigt die Einstellmöglichkeiten der LeCroy-ERES-Mathematik-Funktion sowie den Zusammenhang zwischen Filterlänge, Auflösung und Bandbreitenbegrenzung.
| Erhöhung, Auflösung [Bits] | 3-dB-Bandbreite [× Nyquist] | Filter Länge [Samples] |
|---|---|---|
| 0,5 |
0,5 |
2 |
| 1 |
0,241 |
5 |
| 1,5 |
0,121 |
11 |
| 2 |
0,058 |
25 |
| 2,5 |
0,029 |
52 |
| 3 |
0,016 |
106 |
Tabelle 1. Die Enhanced-Resolution-Filter-Parameter.
Ein kritischer Punkt bei jeder Filterung ist die mathematische Form des verwendeten Filters. ERES berechnet eine neue Funktion, in der jeder Wert in der neuen Funktion aus einem gewichteten Mittelwert von mehreren Punkten der ursprünglichen Kurve berechnet wird.
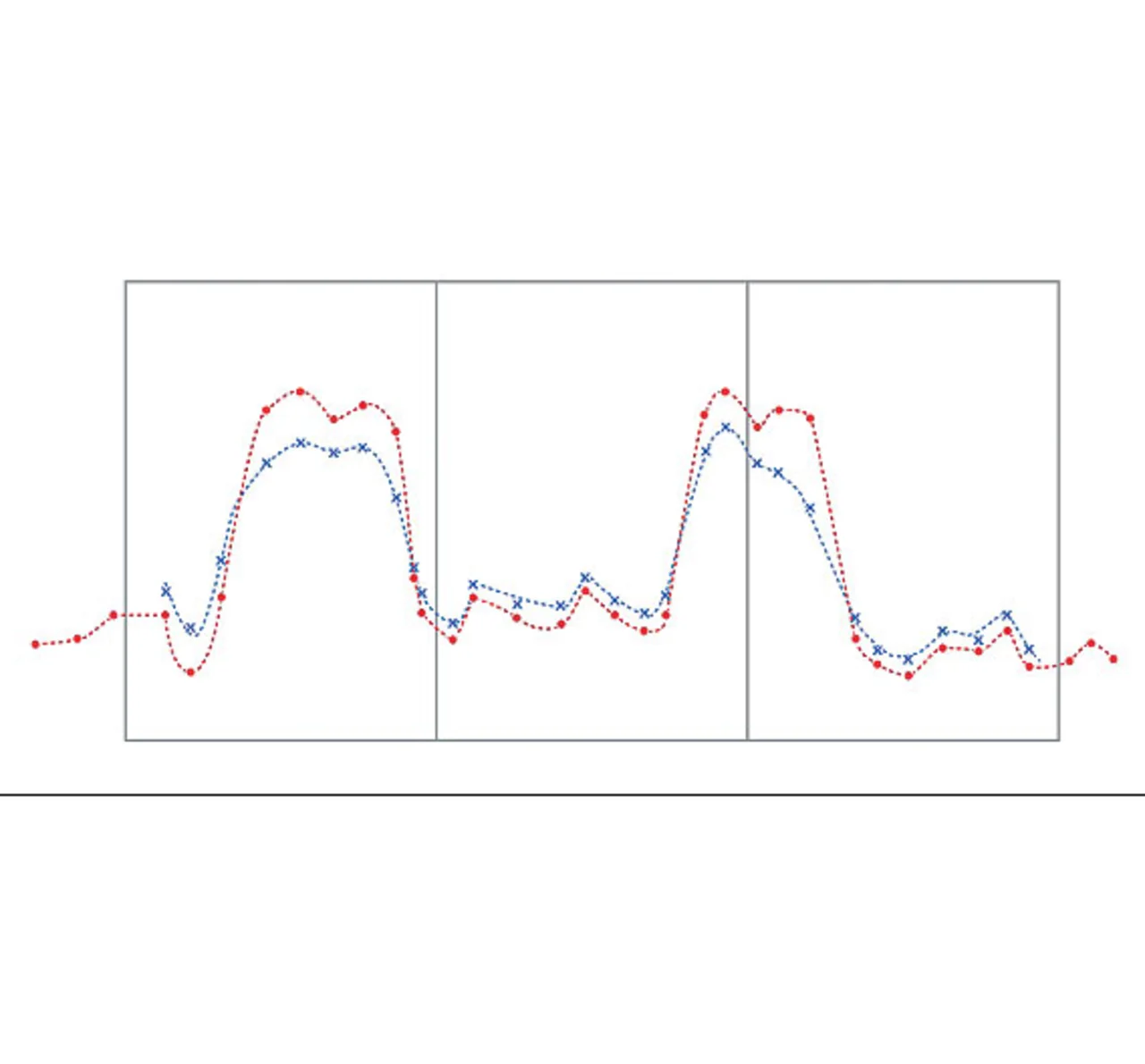
Jeder Sample in dieser neuen Mathematikfunktion wird berechnet aus dem ursprünglichen Abtastwert plus den Samples vor und nach diesem Zeitpunkt, wobei diesen Samples eine geringere Gewichtung gegeben wird. Für die Samples +2 und -2 relativ zum Abtastzeitpunkt wird eine noch geringere Gewichtung gegeben. Dies wird mit abklingender Gewichtung bis zur vollständigen Länge des Filters durchgeführt (Bild 2).
Im Wesentlichen wird den Samples nahe dem ursprünglichen Abtastzeitpunkt eine größere Gewichtung, den Samples weiter davon entfernt eine geringere Gewichtung gegeben. Mathematisch ist jeder neue Punkt eine Summe der Abtastwerte von -N/2 bis +N/2 des A/D-Wandlers, die mit einer glockenförmigen Gewichtung (wobei N die Länge des Filters ist) gewichtet sind. Die neue Mathematikfunktion hat die gleiche Anzahl von Punkten wie die ursprüngliche Funktion, mit der Ausnahme, dass am Anfang und Ende einige Werte für die Filterfunktion wegen fehlendender Punkte nicht berechnet werden können. Somit hat die neue Funktion genau N weniger Punkte als das Original.
Für eine Erfassung mit 100.000 Punkten und einer Erhöhung der Auflösung um 2 Bits entspricht die Filterlänge 25 (Tabelle 1). Somit hat die resultierende ERES-Mathematikfunktion 99.975 Punkte. Normalerweise ist diese Reduzierung der Datenlänge zu kurz, um für die Anwender sichtbar oder störend zu sein.
Abschließend ist über die LeCroy-Implementierung von ERES zu bemerken, dass die einstellbaren ERES-Filter Linear-Phase-FIR-Filter sind, die auf eine schnelle Berechnung, gute Sprung-antwort und minimale Reduzierung der Bandbreite optimiert sind. Der lineare Phasengang bedeutet, dass die Filter nicht die Phasenbeziehung der verschiedenen Frequenzinhalte der Signale verändern, selbst wenn der Frequenzbereich der beiden Funktionen unterschiedlich ist.
Da die Mathematik als eine Post-Processing-Funktion realisiert ist, kann der Benutzer sowohl das ursprüngliche vom A/D-Wandler abgetastete Signal wie auch das ERES-gefilterte Signal darstellen. Falls gewünscht, könnte der Benutzer auch das ursprüngliche Signal und eine Auswahl an verschiedenen Signalen mit unterschiedlicher Filterung darstellen.
- Hohe Auflösung - aber wie?
- Wie funktioniert HiRes?
- Entscheidend: Es wird immer interpoliert
- Erweiterte Anwendungen der Signalfilterung