Startseite > Kommunikation > Wireless > Grundlagen, Ergebnisse und ein Blick auf die Algorithmik

Indoor-Lokalisierung mit Bluetooth 5.1

Grundlagen, Ergebnisse und ein Blick auf die Algorithmik

25. April 2022, 6:00 Uhr | Von Gerrit Maus und Prof. Dr. Dieter Brückmann

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Bestimmung des Einfallswinkels

Um die Qualität und die Möglichkeiten verschiedener Algorithmen zur Bestimmung des Einfallswinkels, d. h. zur Berechnung des AoA, zu demonstrieren, wird im folgenden Beispiel der Einfallswinkel aus Sicht der rechten Station in Bild 4 für eine exemplarische Objektposition berechnet, wie sie ebenfalls im Bild 4 eingezeichnet ist. Aussagekräftige Statistiken zur Qualität der vorgestellten Algorithmen folgen im Absatz »Einfluss des verwendeten Algorithmus«.

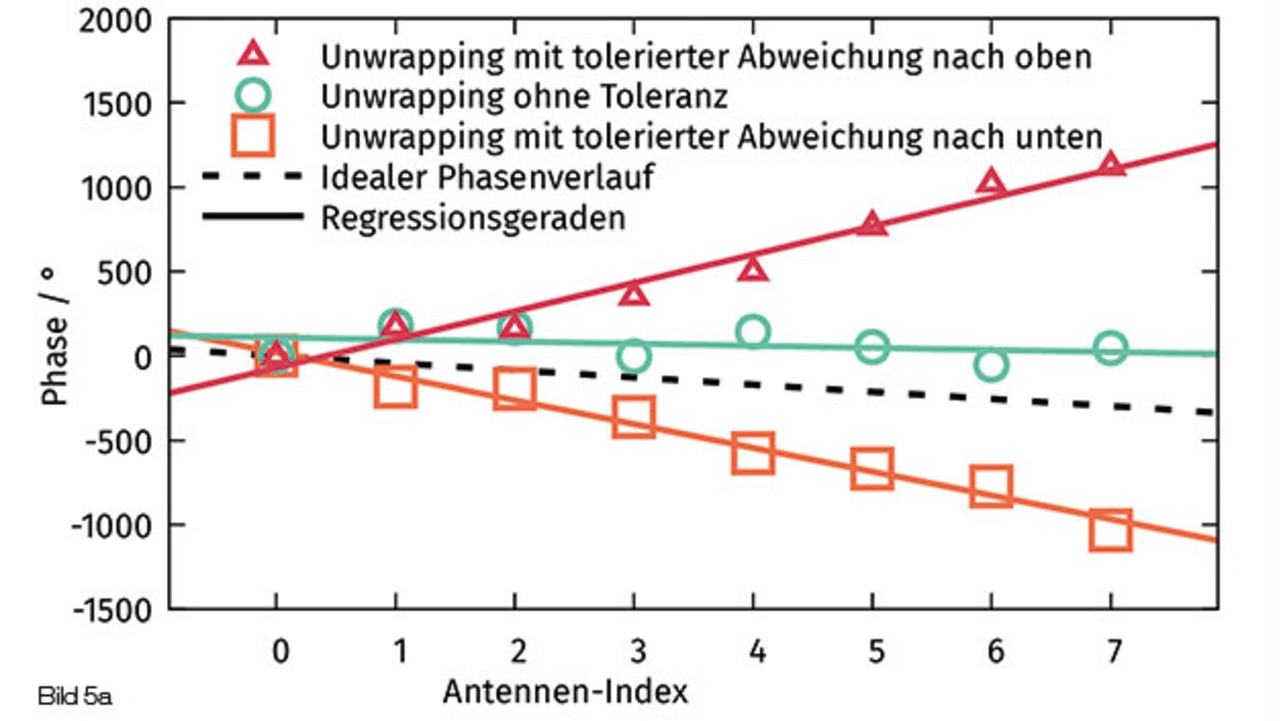
Im einfachsten Fall kann die oben genannte Beziehung zwischen dem Einfallswinkel θ und der Phasendifferenz Δφ genutzt werden, um den Einfallswinkel zu berechnen. Eine Schwierigkeit ergibt sich hierbei aus der richtigen Interpretation der Phasenwerte im gültigen Bereich zwischen z. B. –180 ° und +180 ° bei gleichzeitigem Auftreten von Messunsicherheiten. Die mittlere Datenreihe in Bild 5a zeigt die im obigen Beispiel auf dem ersten Bluetooth-Advertising-Kanal (Trägerfrequenz 2.402 MHz) gemessenen Phasenwerte. Durch das »Abwickeln« der Phasenwerte wird die Beschränkung auf den Bereich ±180 ° aufgehoben, hierzu wurden ganzzahlige Vielfache von 360 ° addiert, sodass sich zwischen zwei aufeinander folgenden Werten eine minimale Differenz ergibt. Dieses Verfahren wird oft auch als »Unwrapping« bezeichnet.

In Gegenwart von Messunsicherheiten trifft diese Interpretation des Gesamt-phasenverlaufs aber häufig nicht zu, insbesondere wenn der tatsächliche Winkel in der Nähe von –90 ° oder +90 ° liegt. Bild 5a zeigt daher noch zwei andere mögliche Interpretationen des Gesamtphasenverlaufs, bei denen eine Abwicklungsabweichung nach unten (hin zu kleineren Phasenwerten) bzw. nach oben (hin zu größeren Phasenwerten) toleriert bzw. forciert wurde, wobei sich die gezeigten Messwerte für jede Antenne lediglich um Vielfache von 360 ° unterscheiden. Diese Interpretationsschwierig-keiten werden dadurch noch verstärkt, dass in der Praxis, insbesondere in Innenräumen, das empfangene Signal den Empfänger typischerweise aus mehreren Richtungen erreicht und so das einfache Modell, was obiger Gleichung für Δφ zugrunde liegt, nicht mehr zutreffend ist.

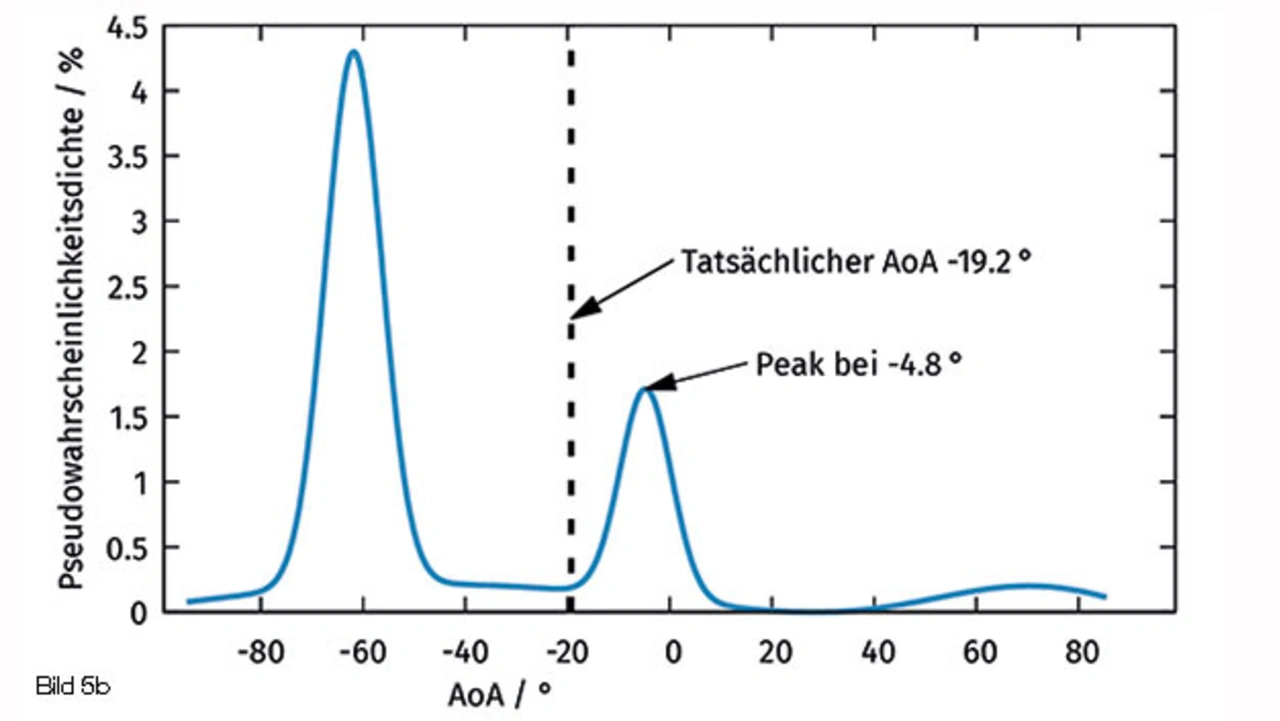
Die sich aus den verschiedenen Interpretationsmöglichkeiten ergebenden Einfallswinkel werden hier durch lineare Regression (Geradenfit) bestimmt. Zur Weiterverarbeitung bietet sich die Berechnung einer Pseudowahrscheinlichkeitsdichteverteilung an, wie sie im Bild 5b zu sehen ist. Hierbei gehen die über lineare Regression bestimmten Einfallswinkel als Gaußverteilung in eine kombinierte Wahrscheinlichkeitsdichte ein, wobei die einzelnen Maxima im Kurvenverlauf gemäß der Qualität der vorherigen Regression (Summe der Fehlerquadrate) gewichtet und gemäß der bestimmten Standardabweichung in der Breite skaliert werden.

Aus den Bildern 5a und 5b ist zu erkennen, dass der tatsächliche Einfallswinkel (–19,2 °) durch eine höchste Wahrscheinlichkeitsdichte bei –61,8 ° stark unterschätzt wurde. Tatsächlich liegt die sekundäre Schätzung mit –4,8 ° besser. Werden die auf diese Weise bestimmten Wahrscheinlichkeitsdichten aller vier Basisstationen zusammengeführt, ergibt sich eine Karte des Testbereichs, die jedem Punkt eine Gesamtwahrscheinlichkeit zuordnet. Der Punkt mit höchster Gesamtwahrscheinlichkeit stellt dann das Resultat des Lokalisierungsprozesses dar, d. h. die geschätzte Position des Objekts. In diesem Beispiel ergab sich zunächst ein Lokalisierungsfehler von 536 cm, der durch Mittelung der Ergebnisse aller drei Bluetooth-Advertising-Kanäle (Trägerfrequenzen 2402, 2426 und 2480 MHz) auf 159 cm verbessert werden konnte.

Ein genauerer Blick auf die im Bild 4 exemplarisch eingezeichneten Ausbreitungspfade kann das unbefriedigende Ergebnis dieses einfachen Ansatzes durchaus erklären. Unter einem Winkel von etwa –60 ° trifft das an der Fensterfront (unten) reflektierte bzw. gestreute Signal auf das Antennen-Array der betrachteten Basisstation. Kann dieser Signalanteil nicht vernachlässigt werden, so ist das obige Modell für Δφ, das nur von einem einzigen Einfallswinkel ausgeht, nicht mehr zutreffend und wird zu fehlerhaften Resultaten führen.

Um die Einfallswinkel in einer solchen Situation bestimmen zu können, wird ein anderer algorithmischer Ansatz benötigt. Eine Möglichkeit besteht in der Verwendung des sogenannten MUSIC-Algorithmus (Multiple Signal Classification) [5]. Hierfür wird zunächst, ähnlich wie oben, ein Modell aufgestellt, das die Abhängigkeit der Messwerte für die einzelnen Antennen von den möglichen Einfallswinkeln beschreibt. Auf Grundlage dieses Modells werden dann die Amplituden- und Phasenmesswerte mittels Eigenwerttheorie auf Bestandteile aller möglichen Einfallswinkel geprüft. Das Ergebnis ist eine Pseudowahrscheinlichkeitsdichteverteilung, wie sie für obiges Beispiel im Bild 6 zu sehen ist.

Auch hier ist der Einfluss des an der Fensterfront reflektierten Signals sichtbar: Die höchste Wahrscheinlichkeitsdichte liegt bei –63,8 °. Ein ausgeprägtes Maximum befindet sich allerdings bei –16,3 °, was dem tatsächlichen Einfallswinkel von –19,2 ° recht nahe kommt. Tatsächlich funktioniert die Ortung des Objekts nach Betrachtung aller vier Wahrscheinlichkeitsdichten deutlich besser als zuvor: Der Lokalisierungsfehler liegt nun im ersten Anlauf bei lediglich 122 cm. Nach Mittelung über alle drei Bluetooth-Advertising-Kanäle ergibt sich eine Lokalisierungsabweichung von nur noch 27 cm.

Ein weiterer Schritt zur Verbesserung der Lokalisierungsqualität liegt in der frühen Berücksichtigung der verschiedenen Bluetooth-Kanäle. In den bisher diskutierten Ansätzen wurden die Informationen aus den verschiedenen Kanälen erst zum Schluss bei der Mittelung der Ergebnisse genutzt. Tatsächlich lässt sich das dem MUSIC-Algorithmus zugrundeliegende Modell aber auch um die Abhängigkeit von der Trägerfrequenz erweitern – und es zeigt sich, dass die Berücksichtigung dieser Kanaldiversität in diesem frühen Stadium vorteilhaft für die Lokalisierungsqualität ist. Dieser Ansatz nennt sich JADE-MUSIC (Joint Angle and Delay Estimation – Multiple Signal Classification) und wird in der für Bluetooth-Systeme modifizierten Form ausführlich in [6] diskutiert.

In Bild 7a ist die Ausgabe dieses JADE-MUSIC-Algorithmus für obiges Beispiel zu sehen. Neben einer AoA-Achse steht nun noch eine weitere Achse zur Verfügung, die die relative Pfadlänge in Bezug auf die Direktverbindung angibt [6]. Gut zu erkennen ist der Einfluss der Direktverbindung, d. h. der Sichtlinie, bei einem Einfallswinkel von etwa –20 ° und einer relativen Pfadlänge von etwa 0. Besonders interessant ist zudem das kleinere Maximum vorne links im Bild bei einem Einfallswinkel von etwa –60 ° und einer relativen Pfadlänge von etwa 3,5 m. Sowohl Winkel als auch Pfadlängendifferenz passen in guter Übereinstimmung zu den im Bild 4 eingezeichneten Signalreflektionen an der Fensterfront.

Nach einer Projektion auf die AoA-Achse, Bild 7b, lassen sich die Ergebnisse wie oben weiterverarbeiten. Nicht nur der Einfallswinkel wurde mit –18,8 ° deutlich genauer geschätzt als mit den bisher besprochenen Methoden. Auch der Lokalisierungsfehler ist mit 9 cm nun deutlich geringer als bisher. Hierfür sind lediglich die Messwerte der drei Bluetooth-Advertising-Kanäle in den Algorithmus eingeflossen, die auch oben schon zur Verfügung standen.