DSP-Algorithmen effizient implementieren – Teil 1 #####
Fortsetzung des Artikels von Teil 3
Phase 3: Anpassung des Algorithmus an den Prozessor
Auf Architekturen wie dem TigerSHARC und dem SHARC haben Divisionen keinen großen Einfluss auf die Gesamtleistung, stellen aber bei Festkomma-Prozessoren eine zeitraubende Prozedur dar. Ein weiteres Beispiel ist das Vorhandensein von Hardware-Beschleunigern auf dem Chip (z.B. FIR-Pipe oder Grafikbeschleuniger), welche dem Prozessorkern bestimmte Aufgaben abnehmen können. So kann ein Algorithmus, der vielleicht mehr Zyklen benötigen würde, dennoch die bessere Alternative sein, da sich bestimmte Teilaufgaben in die Beschleuniger auslagern lassen.
Ein typisches Beispiel für einen Zielkonflikt in dieser Phase ist die Nutzung von iterativen Näherungsverfahren, die eine Abwägung zwischen Genauigkeit und Zyklenzahl erfordert. Hier können die gewonnen Erkenntnisse aus Phase 1 verwendet werden, um diese Entscheidungen für die spezifische Aufgabe zu treffen.
Jobangebote+ passend zum Thema
Gerade für Festkomma-Architekturen (Fixed-Point-Architekturen) sollte der Algorithmus an den Prozessor angepasst werden, da sie bezüglich der Dynamik im Wertebereich, der Präzision der Werte und der Division gegenüber Gleitkomma-Architekturen wie dem SHARC stark eingeschränkt sind. Die Simulation von Gleitkomma-Operationen auf Festkomma-CPUs erfordert eine hohe Zahl an Zyklen, so dass es ratsam ist, bei zeitkritischen Passagen davon Abstand zu nehmen.
In dieser Phase findet auch schon eine erste Abschätzung statt, wie viele Zyklen der Algorithmus optimal brauchen würde. Dafür nimmt man an, man habe eine unbegrenzte Zahl an Registern, und spielt dieses Szenario für die einzelnen Funktionseinheiten durch. Das Ergebnis ist ein Orientierungswert für die spätere Implementierung.
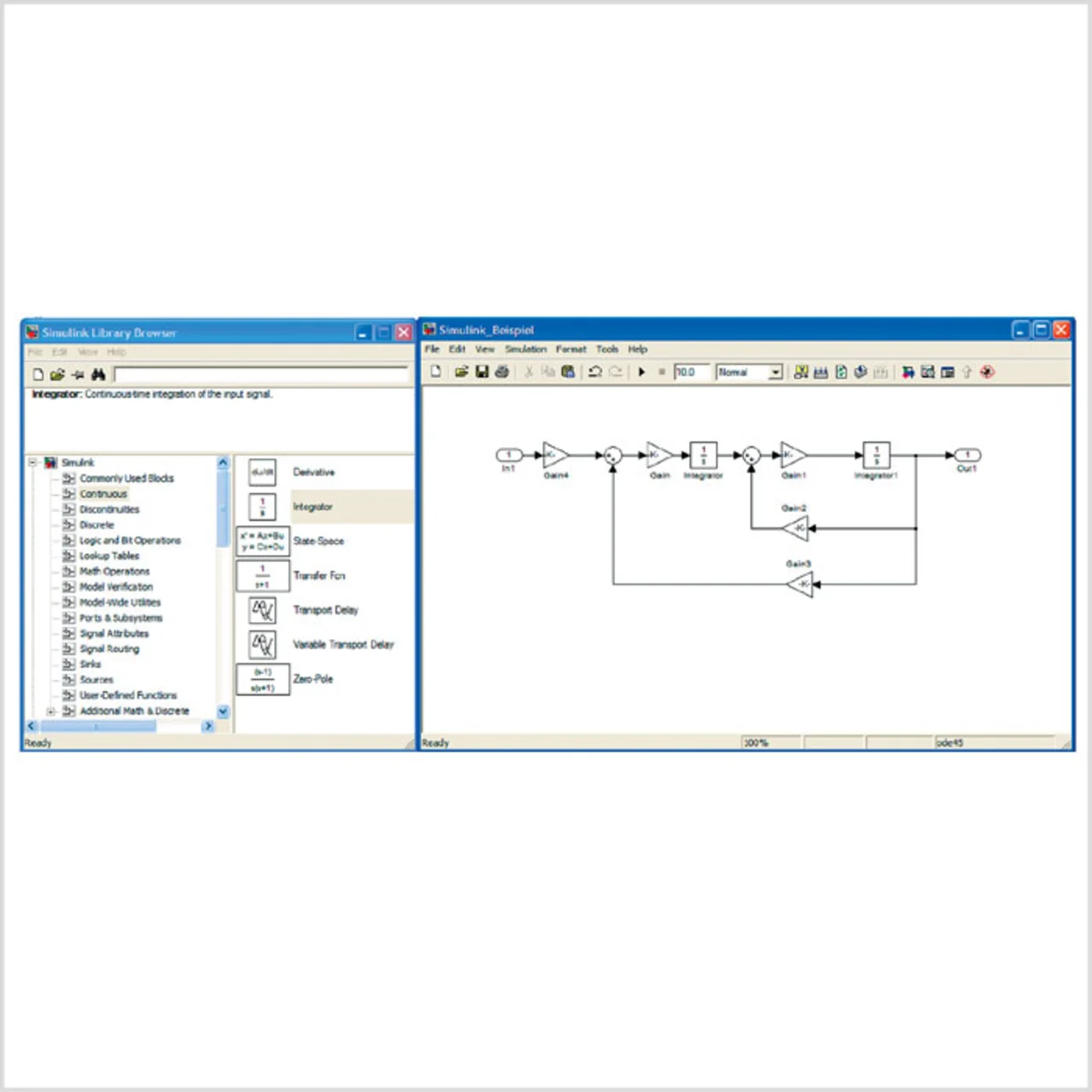
Am Ende dieser Phase kann eine abschließende Simulation auf einem Modellierungs-Tool wie Matlab/Simulink erfolgen, um das Verhalten des Algorithmus in seiner Umgebung zu simulieren und auf diese Weise die Auswirkungen der einzelnen getroffenen Entscheidungen zu evaluieren (Bild 3).
Phase 4: Systemoptimierungen
Das Design der Systemebene stellt einen großen Einflussfaktor bezüglich der Rechenleistung dar. Die Systemebene selbst lässt sich in unterschiedliche Abstraktionsgrade unterteilen:
- Die komplexe Systemebene, welche das gesamte System umfasst und sich zumeist als grobes Blockdiagramm und/oder Ablaufdiagramm darstellen lässt. In der Optimierung lassen sich hier Ansätze der Parallelisierung von unterschiedlichen Prozessen finden. Gerade bei Multiprozessor- oder Multicore-Anwendungen können die Funktionalitäten so auf die einzelnen Recheneinheiten verteilt werden, dass sich hier ein Leistungsgewinn erzielen lässt. Auch mit Hilfe externer Hardware-Beschleuniger kann auf dieser Ebene das System optimiert werden.
- Die Hardware-Ebene kann man als eine wichtige Rahmenbedingung für mögliche Leistungssteigerungen ansehen. So ermöglicht z.B. ein gutes Hardware-Design höhere Taktraten oder den Verzicht auf Waitstates bei Zugriff auf den externen Speicher bzw. auf Systemregister. Ebenso kann die Auswahl der externen Komponenten und Anbindungen (Schnittstellen) das System ausbremsen und sollte auf mögliche Alternativen geprüft werden.
- Die Prozessorebene beinhaltet wichtige Faktoren wie die Speicheraufteilung, das Speichermanagement, die Reaktion auf externe Ereignisse, die Benutzung von Hardware-Beschleunigern und den Systemtakt.
Die folgenden Abschnitte werden sich vorrangig mit der Systemoptimierung auf der Prozessorebene beschäftigen.
- DSP-Algorithmen effizient implementieren – Teil 1 #####
- DSP-Algorithmen effizient implementieren – Teil 1
- Phase 1: Die mathematische Modellierung des Problems
- Phase 3: Anpassung des Algorithmus an den Prozessor
- Bereitstellung von Programm-Code und Daten
- DSP-Algorithmen effizient implementieren – Teil 1