DSP-Algorithmen effizient implementieren – Teil 1 #####
Viele moderne Anwendungen stoßen an die Grenzen der Leistungsfähigkeit heutiger Prozessoren, oder der Kostendruck in einem anversierten Zielmarkt zwingt den Entwickler, auf ein günstigeres, weniger leistungsfähiges System umzusteigen. Um laufzeitkritische Anwendungen...
Viele moderne Anwendungen stoßen an die Grenzen der Leistungsfähigkeit heutiger Prozessoren, oder der Kostendruck in einem anversierten Zielmarkt zwingt den Entwickler, auf ein günstigeres, weniger leistungsfähiges System umzusteigen. Um laufzeitkritische Anwendungen dennoch auf einem solchen System zu implementieren, ist eine darauf hingerichtete Optimierung notwendig. Dieser zweiteilige Artikel stellt ein systematisches Vorgehen bei der leistungsorientierten Optimierung des Programm-Codes anhand der Signalprozessor-Familien von Analog Devices vor.
Jobangebote+ passend zum Thema
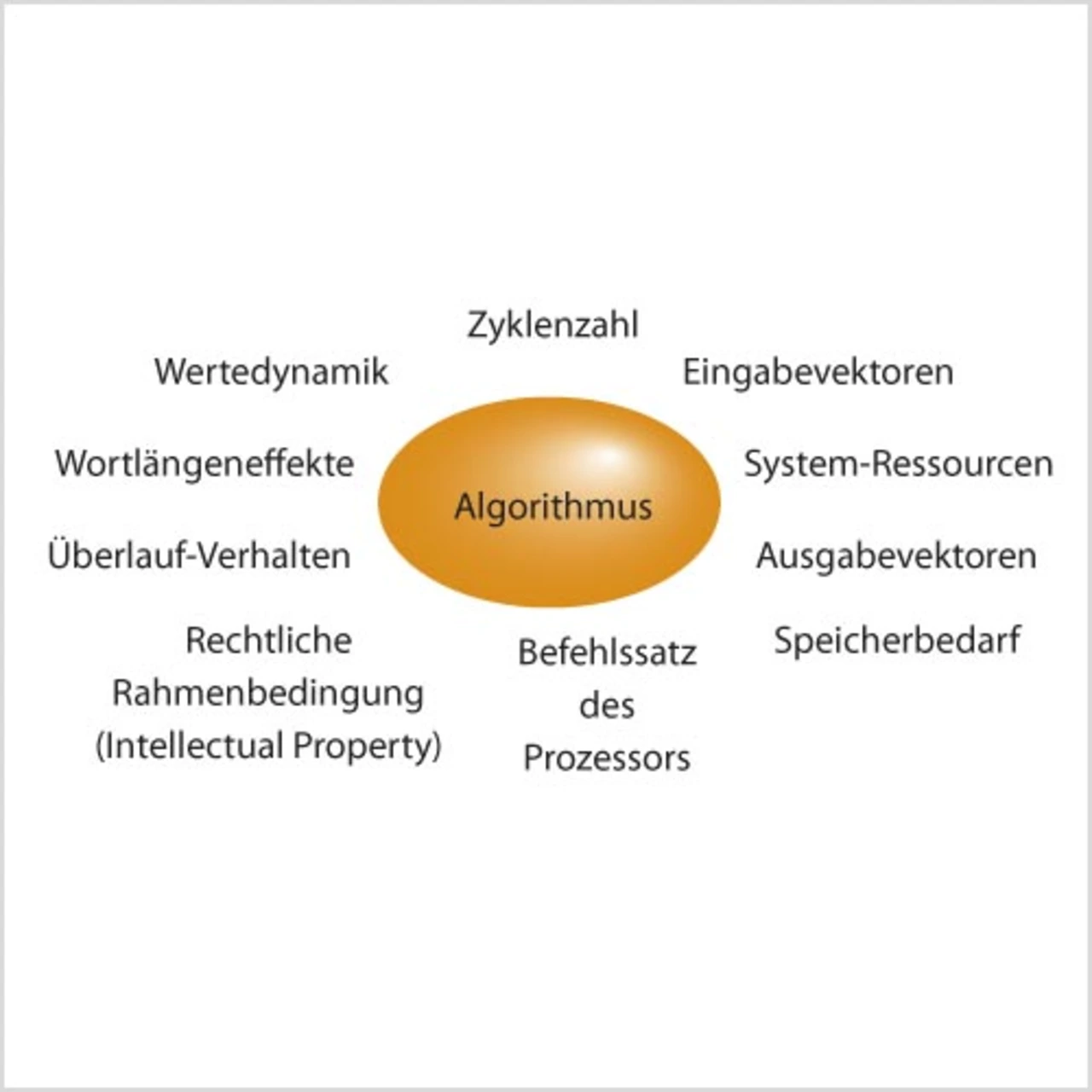
Es gibt zahlreiche Einflussfaktoren auf die Optimierung (Bild 1). Im Folgenden werden die einzelnen Phasen sowie die Vorund Nachteile der Laufzeit-Optimierung vorgestellt. Der zweite Teil des Artikels wird sich vorwiegend den einzelnen Phasen der Implementierung der Algorithmen auf dem Zielsystem widmen.
Digitale Signalprozessoren werden zumeist in Anwendungen eingesetzt, in denen die Bearbeitung einer Aufgabe in Echtzeit erfolgen muss. Diese Aufgaben sind zum größten Teil Algorithmen, welche sich naturgemäß nicht ohne Leistungseinbußen in ANSI-C (American National Standards Institute C) implementieren lassen, da C keine mathematische, an die DSP-Architektur angepasste Beschreibungssprache darstellt. Des weiteren bieten digitale Signalprozessoren zahlreiche Zusatzfunktionen, welche nicht in den Standard-Hochsprachen abgebildet sind. Moderne DSP-Architekturen weisen zudem ein hohes Maß an Parallelität auf, d.h., es können mehrere Funktionen gleichzeitig ausgeführt werden. Diese Komplexität erfordert ein besonderes Vorgehen bei Planung und Implementierung der Anwendungs-Software. Bei dem hier vorgestellten strukturierten, mehrstufigen Software-Entwicklungsprozess ist zu beachten, dass nicht bei jeder Entwicklung zwangsläufig alle Phasen durchlaufen werden müssen. So ist die mathematische Modellierung für viele Probleme schon vorhanden und muss nur noch an die entsprechende Hardware angepasst werden.
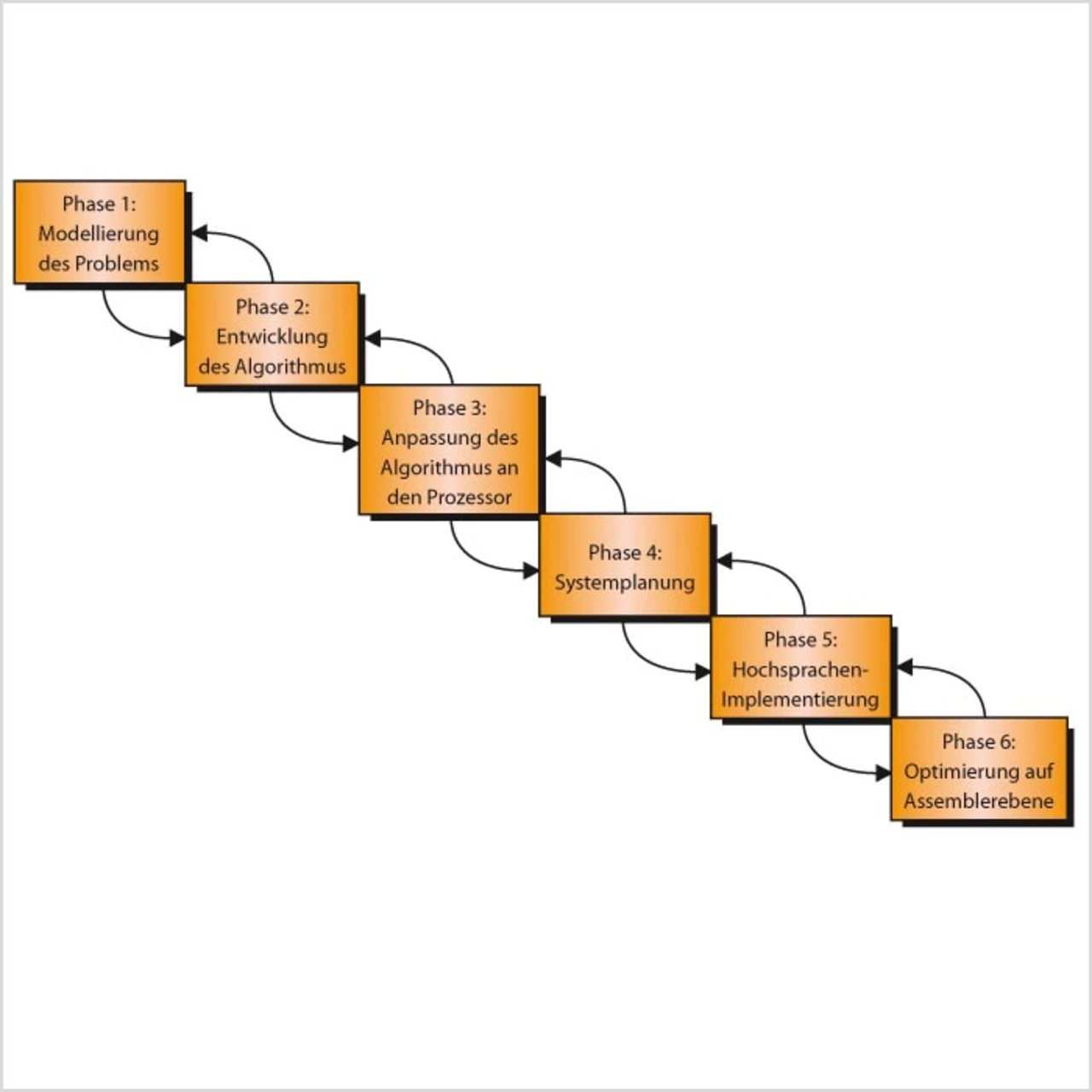
Grob lässt sich der Optimierungsprozess in sechs Phasen bzw. Stufen unterteilen (Bild 2). Eine Rückkehr zu vorigen Stufen sollte jederzeit möglich sein, wenn der gewählte Ansatz sich als unzureichend herausstellt.
Es beginnt mit der (zumeist mathematischen) Modellierung des Problems (Phase 1). Beispiele hierfür sind physikalische Modelle der Außenwelt für die klassische Signalverarbeitung oder die Regelungstechnik oder psychoakustische Modelle für die verlustbehaftete Audio- und Videokompression. Hierbei können schon die ersten Ansätze zur Vereinfachung des Problems gefunden und bestimmte Ein- und Ausgabevektoren ausgeschlossen werden. Aufbauend auf diesen Modellen, können die Algorithmen für die Problemstellung gewählt oder entwickelt werden (Phase 2). Durch die Modellierung des Algorithmus können Optimierungen durchgeführt werden (z.B. aufgrund von Symmetrien).
- DSP-Algorithmen effizient implementieren – Teil 1 #####
- DSP-Algorithmen effizient implementieren – Teil 1
- Phase 1: Die mathematische Modellierung des Problems
- Phase 3: Anpassung des Algorithmus an den Prozessor
- Bereitstellung von Programm-Code und Daten
- DSP-Algorithmen effizient implementieren – Teil 1