Rechnergestützter Entwurf und Simulation von optischen Verbindungen in Leiterplatten
CAD für optische Leiterplatten
Fortsetzung des Artikels von Teil 1
Literatur
| [1] | Schares, L.; Kash, J.A.; Doany, F E.; et al.: Terabus, Terabit/Second-Class Card-Level Optical Interconnect Technology. IEEE Journal of Selected Topics in Quantum Electronics, Vol. 12, 2006, Nr. 5, S. 1032 – 1044. |
| [2] | Schrage, J.; Bierhoff, Th.: Embedded Optical Waveguides for onboard interconnections. Frontiers in Optics, 87th OSA Annual Meeting, Tucson, Arizona, 2003. |
| [3] | Schröder, H.: NeGIT – New Generation Interconnection Technology. Elektronik 2006, H. 14, S. 32 – 35. |
| [4] | Happel, T.; Franke, M.; Nanai, H.; Schrage, J.: Demonstration of optical interconnection- and assembly technique for fully-embedded optical PCB at data rates of 10 GBps/ch. Electronic System Integration Technology Conference, Dresden, 2006. |
| [5] | Hiramatsu, S.; Mikawa, T.: Optical Design of Active Interposer for High-Speed Chip Level Optical Interconnects. IEEE Journal of Lightwave Technology, Vol. 24, 2006, Nr. 2, S. 927 – 934. |
| [6] | Schrage, J.; Sönmez, Y.; Happel, T.; et al.: WDM package enabling high-bandwidth optical intrasystem interconnects. SPIE Photonics West 2006, San Jose, 2006. |
| [7] | Bierhoff, Th.; Himmler, A.; Mrozynski, G.; et al.: Ray Tracing and ist Verification for the Analysis of Highly Multimode Optical Waveguides with Rough Surfaces, Teil 1. IEEE Transaction on Magnetics, Vol. 37, 2001, Nr. 5, S. 3307 – 3310. |
| [8] | Stübbe, O.; Wallrabenstein, A.; Bierhoff, Th.; et al.: Combined simulation of active and passive microoptical components. Microoptics Conference (MOC), Tokio, 2005. |
| [9] | Bierhoff, Th.; Sönmez, Y.; Schrage, J.; et al.: Fundamental limits of the bandwith-length product of board-integrated optical multimode waveguides due to intermode dispersion. Optics in Computing 2004, Engelberg, Schweiz, 2004. |
| [10] | Koshiba, M.: Optical Waveguide Theory by Finite Element Method. KTK Scientific Publisher, 1. Auflage, 1992. |
| [11] | Kawano, K.; Kitho, T.: Optical Waveguide Analysis – Solving Maxwell’s Equations and the Schrödinger Equation. 1. Auflage, Wiley, 1992. |
| [12] | Lehner, G.: Elektromagnetische Feldtheorie. 2. Auflage, Springer Verlag, 1994. |
| [13] | Bierhoff, Th.: Strahlenoptische Analyse der Wellenausbreitung und Modenkopplung in optisch hoch multimodalen Wellenleitern. 1. Auflage, Shaker Verlag, 2006. |
| [14] | Shannon, R.R.: The Art and Science of Optical Design. Cambridge University Press, 1997. |
| [15] | Lambda Research Corp., Ray-Tracing Software TracePro, www.lambdares.com. |
| [16] | Zemax Development Corp., Ray-Tracing Software Zemax, www.zemax.com. |
| [17] | Voges, E.; Petermann, K.: Optische Kommunikationstechnik. Springer Verlag, 2002. |
| [18] | Neyer, A.; Kopetz, S.; Rabe, E.: Lichtwellenleiter aus Silikon. Elektronik 2005, H. 9, S. 40 – 46. |
| [19] | Schubert, H.: FR4-kompatible optische Leiterplatte. Elektronik 2004, H. 12, S. 37 – 38. |
| [20] | Griese, E.: Optische SPICE-Modelle. Elektronik 2004, H. 6, S. 58 – 63. |
| [21] | Scheel, W.: Leiterplatte als High-Tech-Bauelement. Elektronik 2003, H. 9, S. 80 – 85. |
| [22] | Eifer, B.: Backplanes für Elektronen und Photonen. Elektronik 2003, H. 9, S. 86 – 89. |
| [23] | Gerdom, K.; Bussmann, R.: Elektrische Steckverbinder für optische Signale. Elektronik 2002, H. 21, S. 48 – 52. |
| [24] | Demmer, P.: Lichtleiter statt Leiterbahnen. Elektronik 2002, H. 13, S. 148 – 151. |
| [25] | Ishak, W.: Optische Systeme auf einem Chip. Elektronik 2002, H. 13, S. 158 – 164. |
| [26] | Schmale, I.: Parallele Optik im Aufwind. Elektronik 2002, H. 12, S. 62 – 67. |
| [27] | Lemme, H.: Optische Signale von Chip zu Chip. Elektronik 2001, H. 12, S. 42 – 48. |
 | Dr.-Ing. Thomas Bierhoff studierte Elektrotechnik an der Universität Paderborn und promovierte am Fachgebiet Theoretische Elektrotechnik über die numerische Simulation der Wellenausbreitung und Modenkopplung in optisch vielmodigen Wellenleitern mit rauhen Kerngrenzflächen. Seit 2004 ist er im Forschungs- und Entwicklungslabor C-LAB der Siemens IT Solutions and Services GmbH & Co. OHG tätig. Hier ist er verantwortlich für die Entwicklung von Entwurfsund Simulationswerkzeugen für optische Intra-Systemverbindungen in Leiterplatten. thomas.bierhoff@c-lab.de |
 | Dr.-Ing. Jürgen Schrage studierte Elektrotechnik und promovierte am Paderborner Heinz Nixdorf Institut über die Analyse von Crosstalk-Problemen in hochintegrierten digitalen Schaltungen. 1999 trat er bei Siemens ein und leitete seither u.a. die nationalen bzw. europäischen Verbund-Forschungsprojekte „OptoSys“ und „HOLMS“ über optische Intrasystem-Verbindungstechnik. Seit 2002 ist er Leiter des Arbeitsgebiets Optical Interconnection Technology im C-LAB, dem Innovation Center des Siemens-Bereichs IT Solutions and Services und der Universität Paderborn. juergen.schrage@c-lab.de |
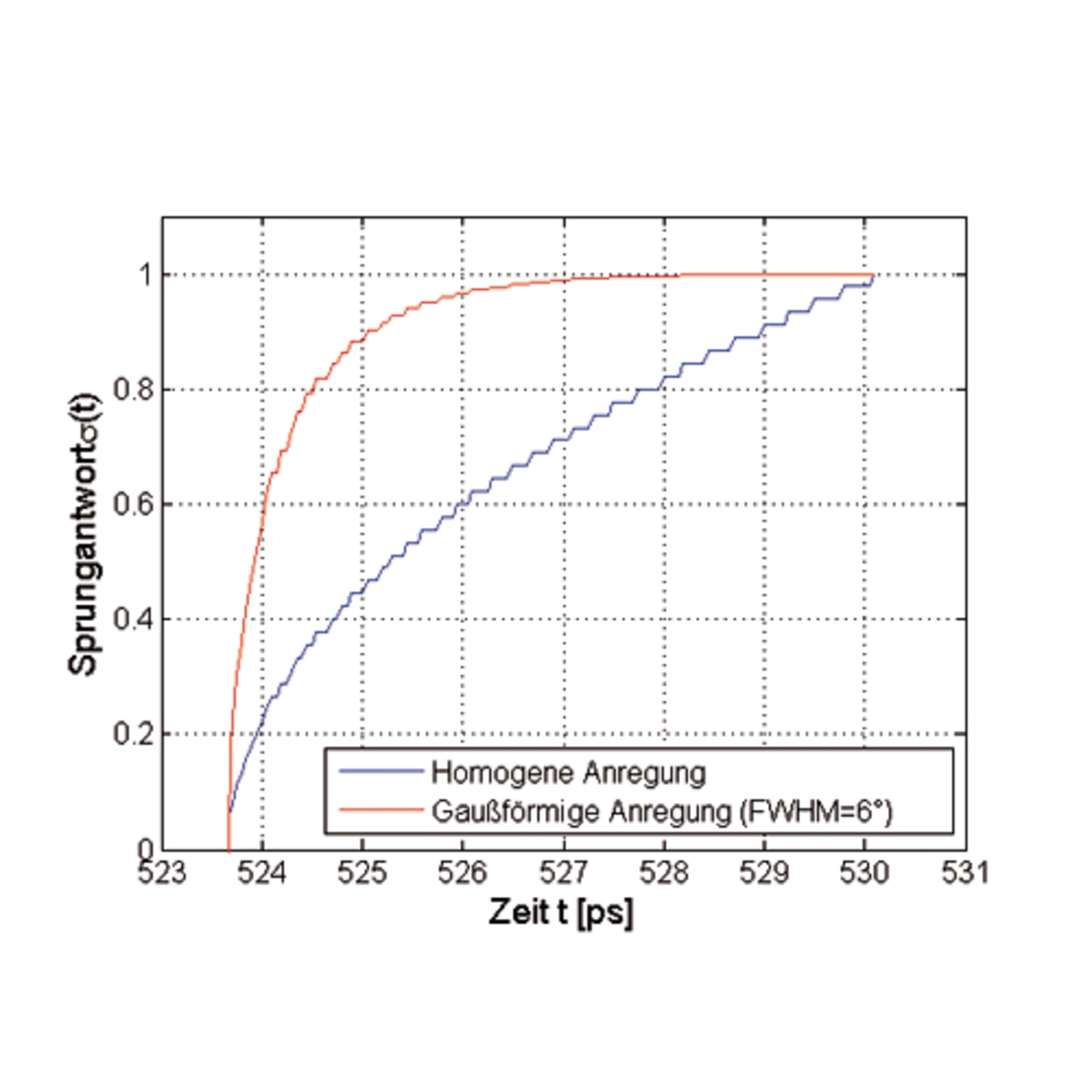
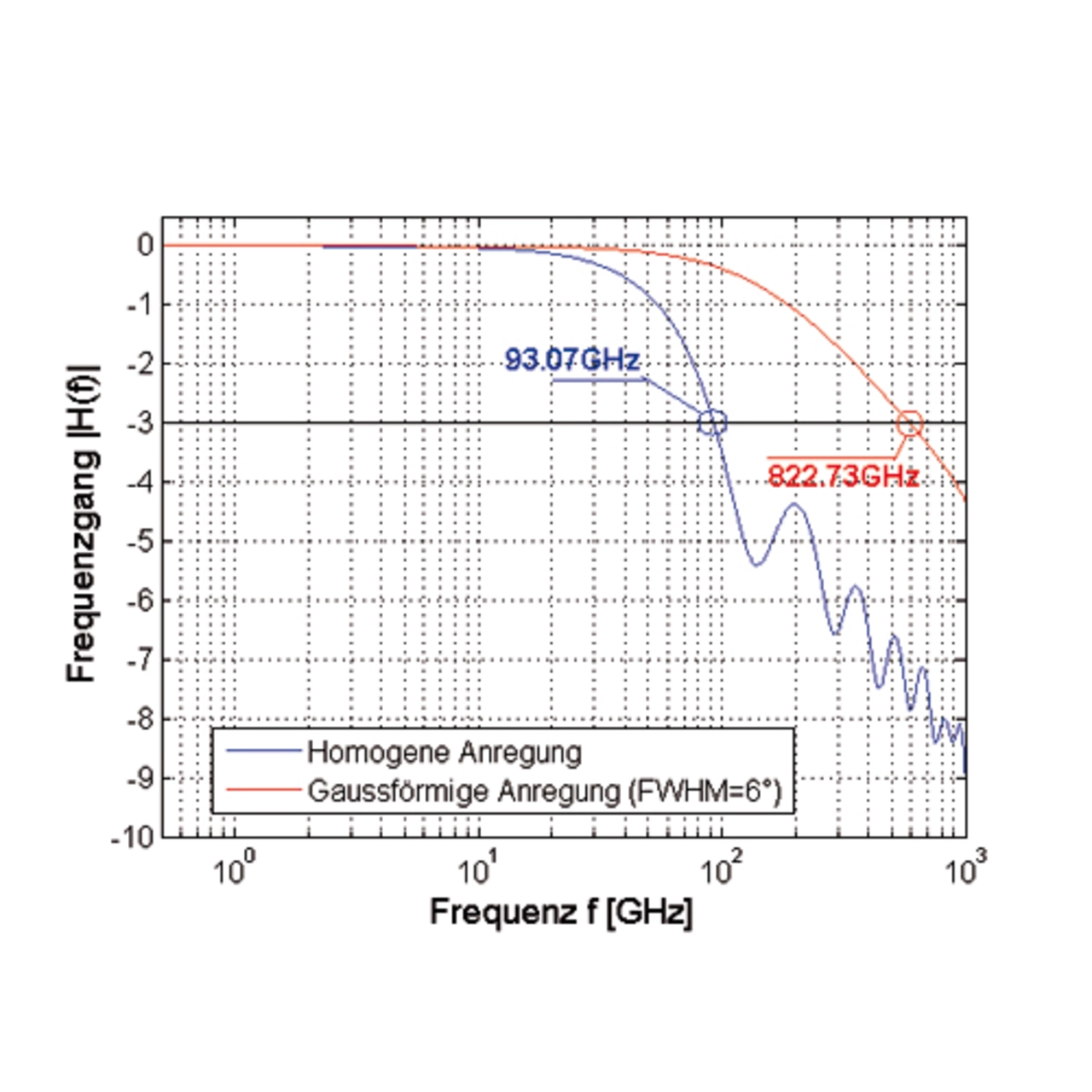
Aufgrund der großen transversalen Kernabmessungen planar integrierter Wellenleiter und ihrer großen numerischen Apertur von mehr als 0,2 wird ihr maximal erreichbares Bandbreitenlängenprodukt aufgrund der Intermodendispersion limitiert [17]. Um auch hier eine quantitative Aussage bezüglich der Übertragungsbandbreite machen zu können, wurden die transienten Übertragungseigenschaften eines geraden Wellenleiters mit einer numerischen Apertur von 0,25 simuliert und die resultierenden Sprungantworten ausgewertet. Dabei wurden zwei unterschiedliche räumliche Emissionspektren der optischen Quelle verwendet, die zum einen die numerische Apertur homogen und zum anderen gaußförmig mit einer Winkelbreite von 6° (FWHM) ausleuchten – Full Width Half Maximum (FWHM) repräsentiert die Winkelbreite des Fernfeldes eines räumlichen Emissionsspektrums einer optischen Quelle, bei der die emittierte Leistung auf die Hälfte abgesunken ist. Ersterer Fall entspricht einer Worst-case-Anregung hinsichtlich der Signalübertragung und dient der Vorhersage eines minimalen Bandbreitenlängenproduktes. Der zweite Fall bildet in guter Näherung die Anregung durch einen Einmodenlaser nach und stellt somit eine realistische Vorhersage des Bandbreitenprodukts dar. Die beiden Sprungantworten wurden nach einer Wellenleiterlänge von 10 cm durch optische Simulationen bestimmt und sind in Bild 10a dargestellt. Um aus diesen die Bandbreitenlängenprodukte extrahieren zu können, wurden sie nach der Zeit abgeleitet und die resultierenden Ergebnisse durch eine Fouriertransformation in den Frequenzbereich transformiert. Die hierdurch erhaltenen Übertragungsfunktionen sind in Bild 10b dargestellt.
Jobangebote+ passend zum Thema
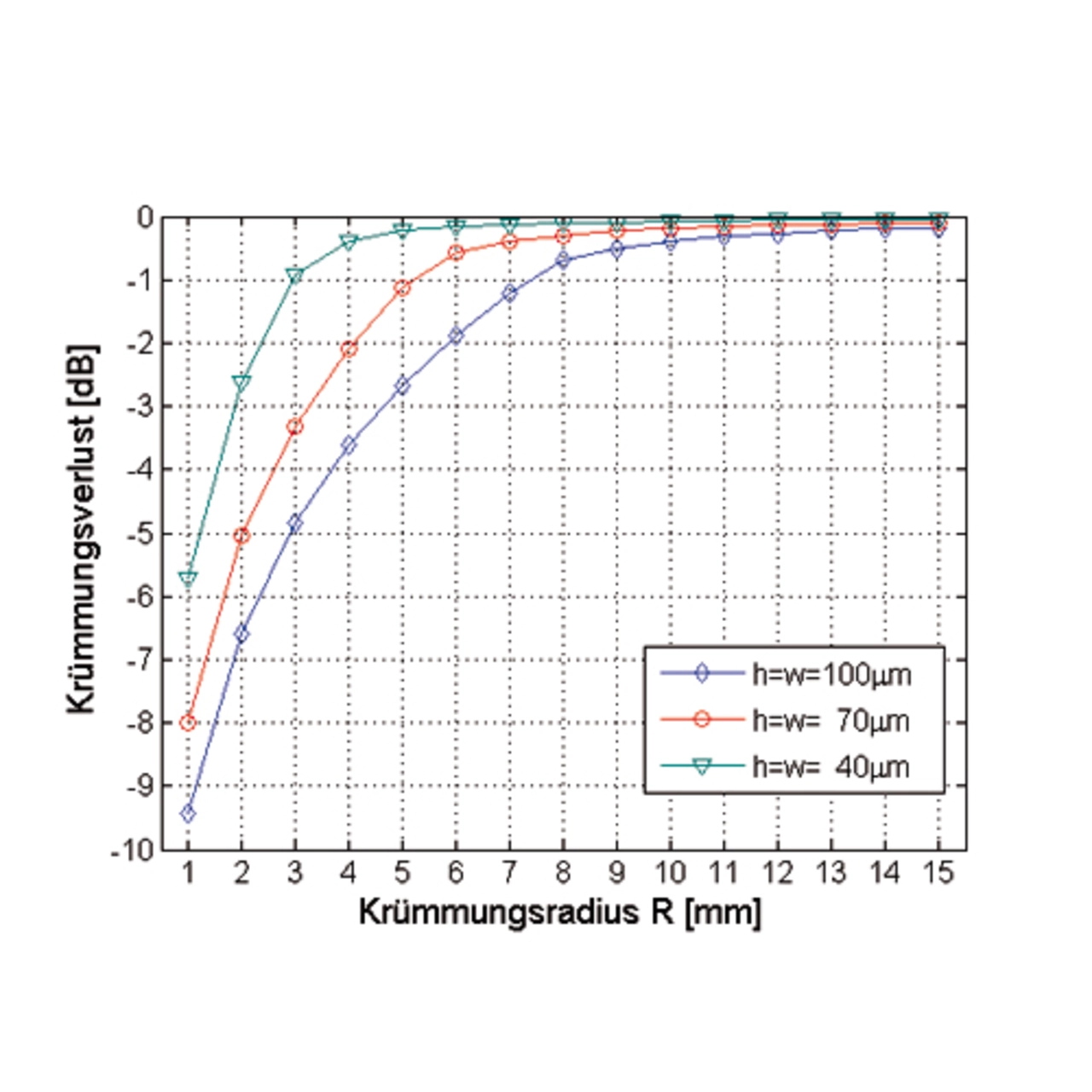
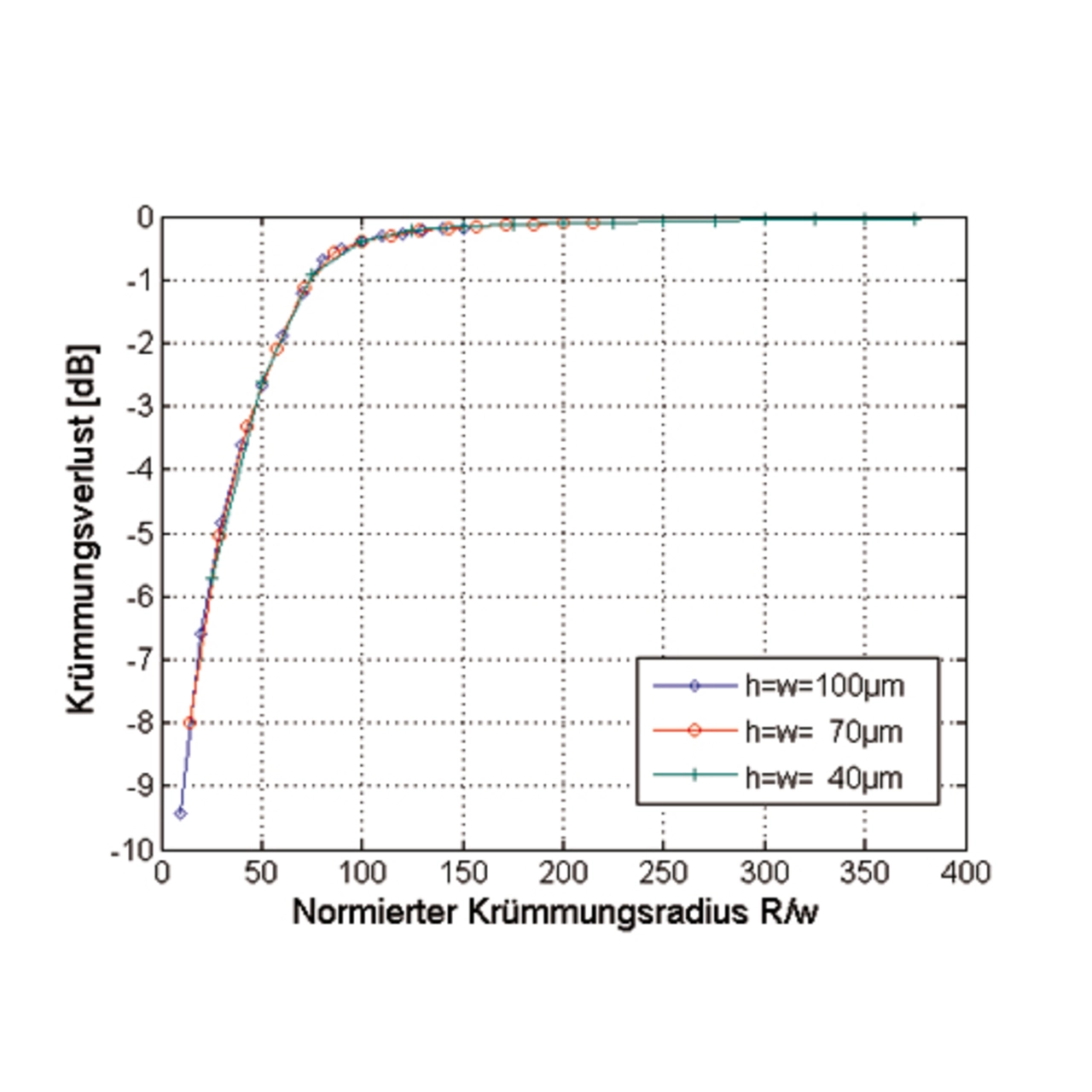
Durch Auswerten der 3-dB-Grenzfrequenz können dann die erreichbaren Bandbreitenlängenprodukte für eine Wellenleiterlänge von 0,1 m extrahiert werden. In [13] wird bewiesen, dass das Bandbreitenlängenprodukt für unterschiedliche Wellenleiterlängen konstant ist, so dass durch eine Extrapolation das Bandbreitenlängenprodukt auch für einen Meter angegeben werden kann. Diese durchgeführten Simulationen zeigen deutlich zwei wesentliche Eigenschaften planar integrierter optischer Wellenleiter auf. Zum einen weisen sie eine Bandbreitenbegrenzung auf und zum anderen wird diese Bandbreitenbegrenzung neben einer Reihe weiterer Parameter auch stark von dem anregenden räumlichen Emissionspektrum der Quelle beeinflusst.
So schwanken die hier numerisch berechneten Bandbreitenlängenprodukte für die beiden verwendeten Emissionspektren von 9,3 GHzm und 82,2 GHzm. Dies verdeutlicht sehr eindringlich die Notwendigkeit des ganzheitlichen Simulationsansatzes, der auch die Eigenschaften der optischen Quellen zu berücksichtigen hat.
- CAD für optische Leiterplatten
- Literatur
- CAD für optische Leiterplatten
- CAD für optische Leiterplatten
- CAD für optische Leiterplatten
- CAD für optische Leiterplatten
- Entwurf und Simulation optischer Verbindungen erfordern ganzheitliche Sichtweise