Feldorientierte Antriebssteuerung
Sensor regelt Motor
Fortsetzung des Artikels von Teil 2
Sensor regelt Motor
Weshalb FOR?
Die skalare Regelung des sechsschrittigen Kommutierungsprozesses, mit dem ursprünglich BLDC-Motoren auf der Basis von Hallsensor-Signalen (aber auch in sensorloser Technik) geregelt wurden, hat eine hohe Stelldynamik. Sie bestromt ein Wicklungspaar erst dann, wenn der Motor die nächste Stellung erreicht, und wechselt dann zum nächsten Kommutierungsschritt.
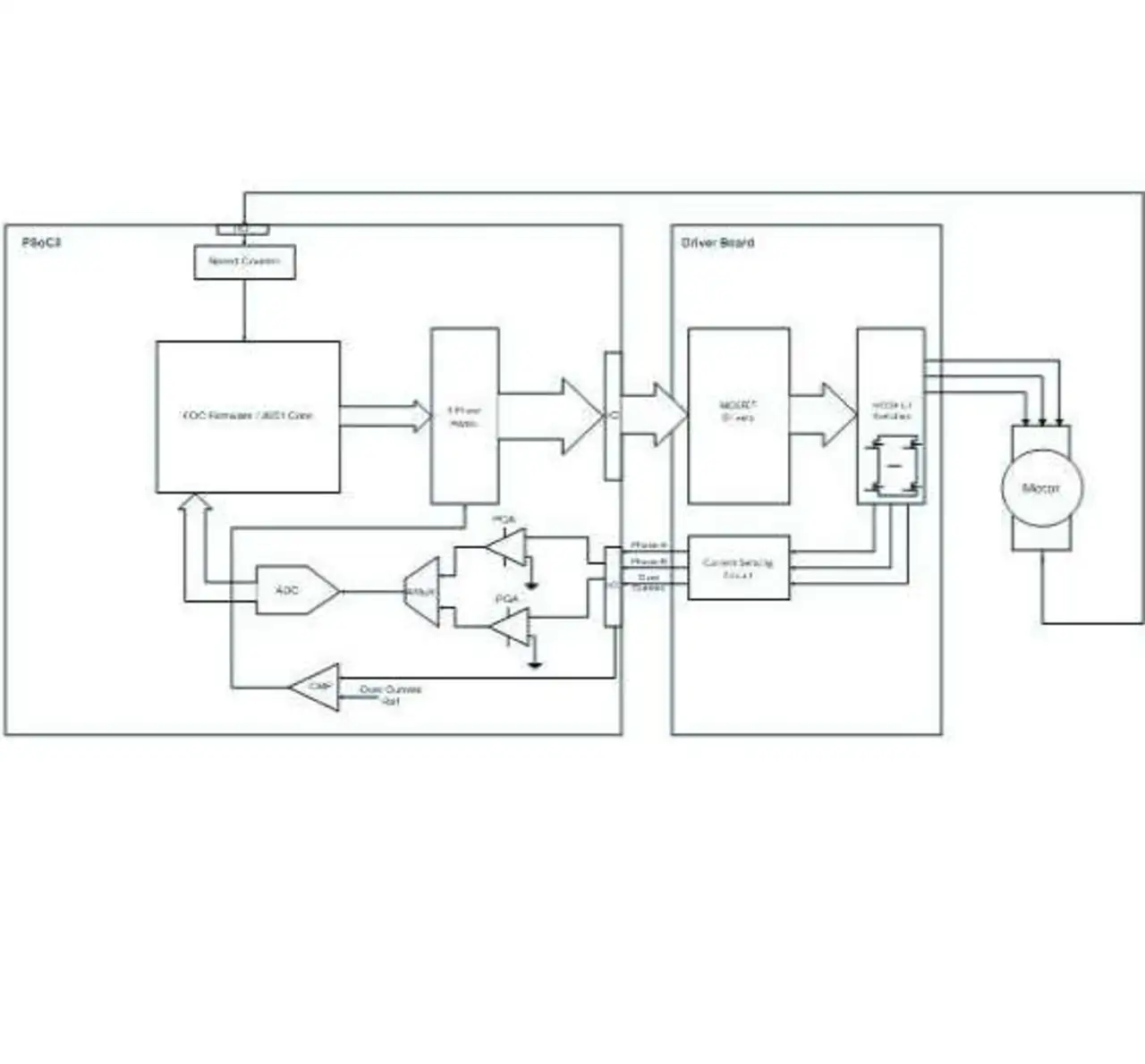
In einer Implementierung mit Sensoren erfassen Halleffekt-Sensoren die Rotorstellung, um den Motor entsprechend zu kommutieren. Der Vorteil der skalaren Regelung ist ihre einfache Implementierung. Eine Reihe fortschrittlicherer skalarer Regelungsmethoden nutzt die vom Motor erzeugte Gegen-EMK, um die Rotorstellung zu bestimmen.
Die damit erzielte Stelldynamik eignet sich indes nicht für Anwendungen, in denen sich die Last während eines Zyklus‘ dynamisch ändert. Diese dynamischen Laständerungen bewältigen nur ausgefeiltere Algorithmen wie die feldorientierte Regelung. Nachfolgend wird die Implementierung eines FOR-Algorithmus’ an einem Beispiel auf Basis des programmierbaren Bausteins »PSoC 3« von Cypress demonstriert.
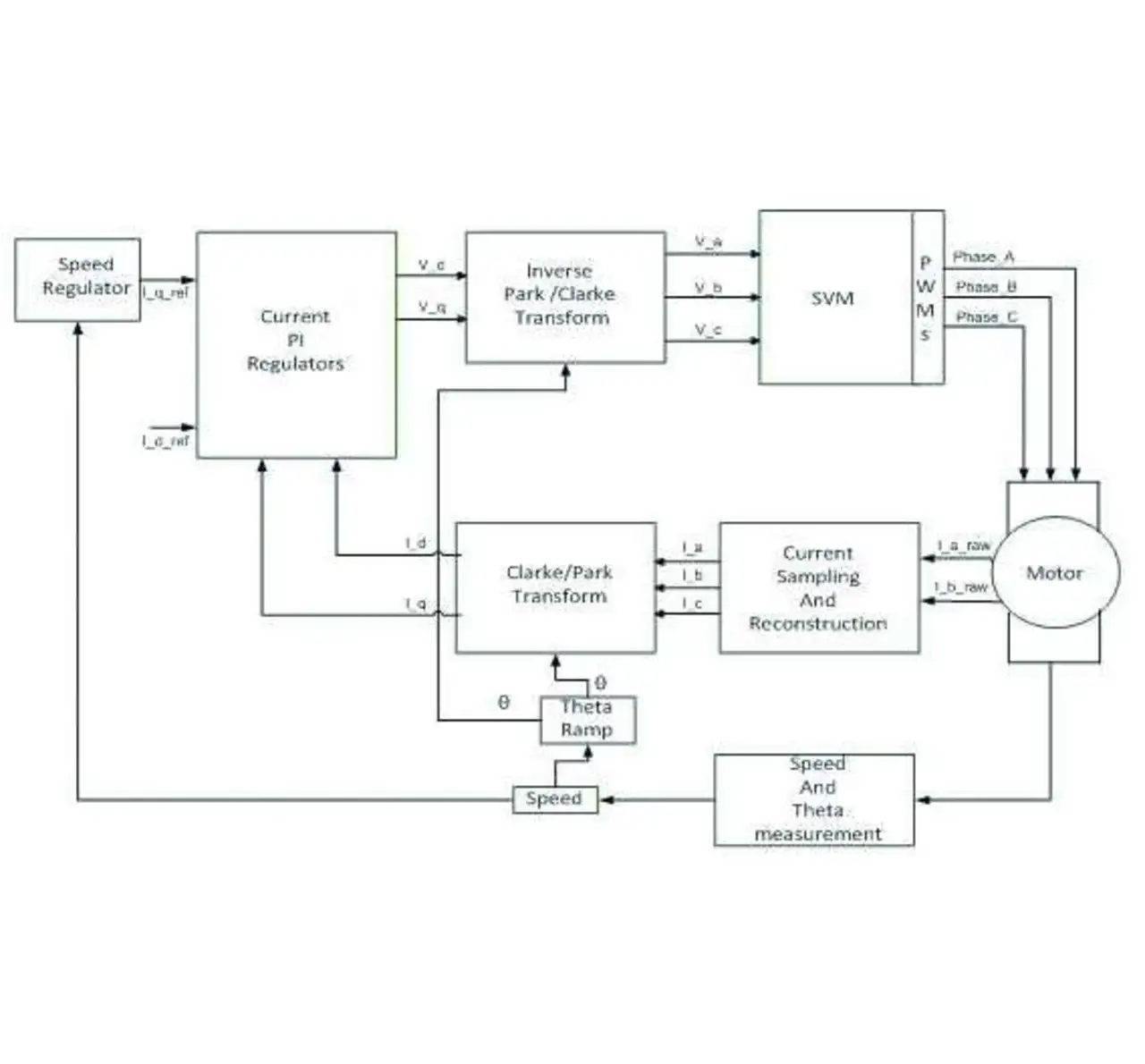
Das Subsystem (Bild 3) gliedert sich in die folgenden Hauptmodule (Bild 4):
1. Stromrekonstruktions-Modul: Zur Rekonstruktion der Ströme wird eine Methode auf der Basis zweier Shunts verwendet. Die Messung der Ströme geschieht in zwei Zweigen, während der dritte nach den Kirchhoffschen Regeln rekonstruiert wird. Die PWM-Signale sind zentriert angelegt, und beide Ströme werden in jedem FOR-Zyklus jeweils in der Mitte der PWM-Periode abgetastet. Der FOR-Algorithmus veranlasst anschließend die Digitalisierung der Signalproben und rekonstruiert die Ströme.
2. Clarke- und Park-Transformationen: Die rekonstruierten Ströme werden anschließend mit der Clarke-Transformation in ein zweiachsiges statorbezogenes Koordinatensystem und anschließend mit der Park-Transformation in ein zweiachsiges rotorbezogenes Koordinatensystem transformiert. Nach Abschluss dieser Transformationen erfüllt der Strom im rotorbezogenen Koordinatensystem alle Voraussetzungen, um entsprechend den Drehzahl- und Drehmomentvorgaben geregelt zu werden.
3. PI-Regler: Zur Regelung des zweiphasigen Rotor-Referenzstroms und der Motordrehzahl wurden allgemeine PI-Regler mit einstellbarer Verstärkung und Min/Max-Sättigung implementiert.
4. Inverse Park- und Clarke-Transformationen: Das geregelte Ausgangssignal wird anschließend mit inversen Park- und Clarke-Transformationen wieder in eine Dreiphasen-Referenz (PWM-Tastverhältnis) zurückverwandelt, um die Drehzahl des Motors zu variieren.
5. Raumzeigermodulation: Durch dieses Verfahren wird eine Sinuswelle erzeugt, mit der die Statorspulen angesteuert werden. Gestützt auf das mithilfe der inversen Clarke-Transformation erzeugte dreiachsige Bezugssystem, generiert die Raumzeigermodulation die PWM-Compare-Werte, die jeweils um 120° phasenversetzt sind (Gleichung (2)),
PWM«/mi»«mi»Period«/mi»«/msub»«mo»-«/mo»«mn»2«/mn»«mo»§#183;«/mo»«mo»(«/mo»«msub»«mi»T«/mi»«mn»1«/mn»«/msub»«mo»+«/mo»«msub»«mi»T«/mi»«mn»2«/mn»«/msub»«/mrow»«mn»2«/mn»«/mfrac»«/math»" align="middle">
hier ist tb = tc + 2T1 und ta = tb + 2T1). tc, tb und ta sind die Werte in den PWM-Compare-Registern (Tabelle 2), T1 und T2 ergeben sich aus Tabelle 1; PWMperiod ist die Zahl der PWM-Perioden.
| Sektor | T1 | T2 |
|---|---|---|
| 1 |
-Vb |
-Vc |
| 2 | -Vc | -Va |
| 3 | Vb | Va |
| 4 | -Va | -Vb |
| 5 | Va | Vc |
| 6 |
Vc |
Vb |
Tabelle 1. Wertetabelle zur Ermittlung von T1 und T2, Va, Vb und Vc sind die Ausgangswerte der inversen Clarke-Transformation
| Sektor | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| PWM_A | tb | ta | ta |
tc |
tc |
tb |
| PWM_B | ta | tc | tb | tb | ta | tc |
| PWM_C | tc | tb | tc |
ta |
tb |
ta |
Tabelle 2: Wertetabelle zur Zuweisung des PWM-Tastverhältnisses
Erfassung von Drehzahl und Rotorposition
Die Drehzahl wird aus dem zeitlichen Abstand zwischen zwei steigenden oder fallenden Flanken eines Hallsensor-Signals hergeleitet. Diese elektrische Periodendauer ist der Kehrwert der elektrischen Frequenz beziehungsweise der Drehzahl. Durch Aufsummieren dieses elektrischen Drehzahlwertes in jedem FOR-Zyklus lässt sich die Rotorposition θ ermitteln.
Im vorliegenden Beispiel dauert ein FOR-Zyklus 200 μs. Es gilt die Beziehung θ = ωt, wobei θ der Winkelabstand in Sekunden ist, ω die Winkelgeschwindigkeit und t das Zeitintervall für die Berechnung von θ. Die Rotorposition θ lässt sich anstatt mit Hallsensoren auch mit einem Encoder ermitteln, der die Information ohne Aufsummieren der Drehzahl direkt ausgibt.
- Sensor regelt Motor
- Sensor regelt Motor
- Sensor regelt Motor
Lesen Sie mehr zum Thema
