Startseite > Power > Spannungswandler > Küchengeräte ohne Netzkabel – Küchen ohne Steckdose

Wireless Power

Küchengeräte ohne Netzkabel – Küchen ohne Steckdose

5. März 2018, 10:45 Uhr | Mahesh Itraj und Will Ettes

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Anforderungen eines Wireless-Power-System für Küchen

Der vorige Abschnitt ging auf die derzeit verwendete Serienresonanz-Schaltung ein. Sie kann zwar hohe Leistungen mit hohem Wirkungsgrad übertragen, aber es ist schwierig, mit ihr die nicht funktionsbezogenen Anforderungen der Wechselrichterstufe zu erfüllen, z.B. hinsichtlich EMI.

In einem Wireless-Power-System für Küchenarbeitsplatten bleibt der Sender (Tx) stets derselbe, wogegen sich der Empfänger (Rx) ändert, abhängig davon welches Gerät auf der Arbeitsplatte abgestellt wird. Es ist somit vorteilhaft, den Nachteil der Serienresonanz-Schaltung für Wireless-Power-Küchensysteme so zu minimieren, dass nur die Senderseite modifiziert werden muss. Deshalb werden nachfolgend nur verschiedene Senderschaltungen analysiert, der Empfängerteil bleibt unverändert.
Die grundlegende Anforderung an die neue Senderschaltung lautet, dass sie von sich aus alle nicht funktionsbezogenen Anforderungen erfüllen soll, ohne dass dafür Abstriche am Wirkungsgrad gemacht werden müssen.

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

Wie weiter oben im Text erwähnt, kann das Variieren des Tastverhältnisses dazu führen, dass die Leistungsschalter nicht mehr im Spannungs-Nulldurchgang schalten, was zu steilen Spannungsflanken an den Knoten der Brückenschaltung führt. Die zeitliche Änderung des Eingangsstroms (dI/dt) und die zeitliche Änderung der Spannung an der Senderspule (dU/dt) können EMI-Probleme verursachen. Hieraus resultiert die erste Forderung an das Wireless-Power-System nach geringen elektromagnetischen Interferenzen. Die an die Senderschaltung gestellten Anforderungen lassen sich deshalb wie folgt zusammenfassen:

Funktionsbezogene Anforderungen:
- Leistungsübertragung bis 2,4 kW
- Wirkungsgrad über 90 %
- Einfache Regelung
Die wichtigste nicht funktionsbezogene Anforderung lautet:
- wenig Störsignale (EMI)

Gemäß diesen Anforderungen wird in den weiteren Abschnitten eine neue Schaltung erarbeitet und analysiert.

Schaltung mit geringem Störsignalaufkommen

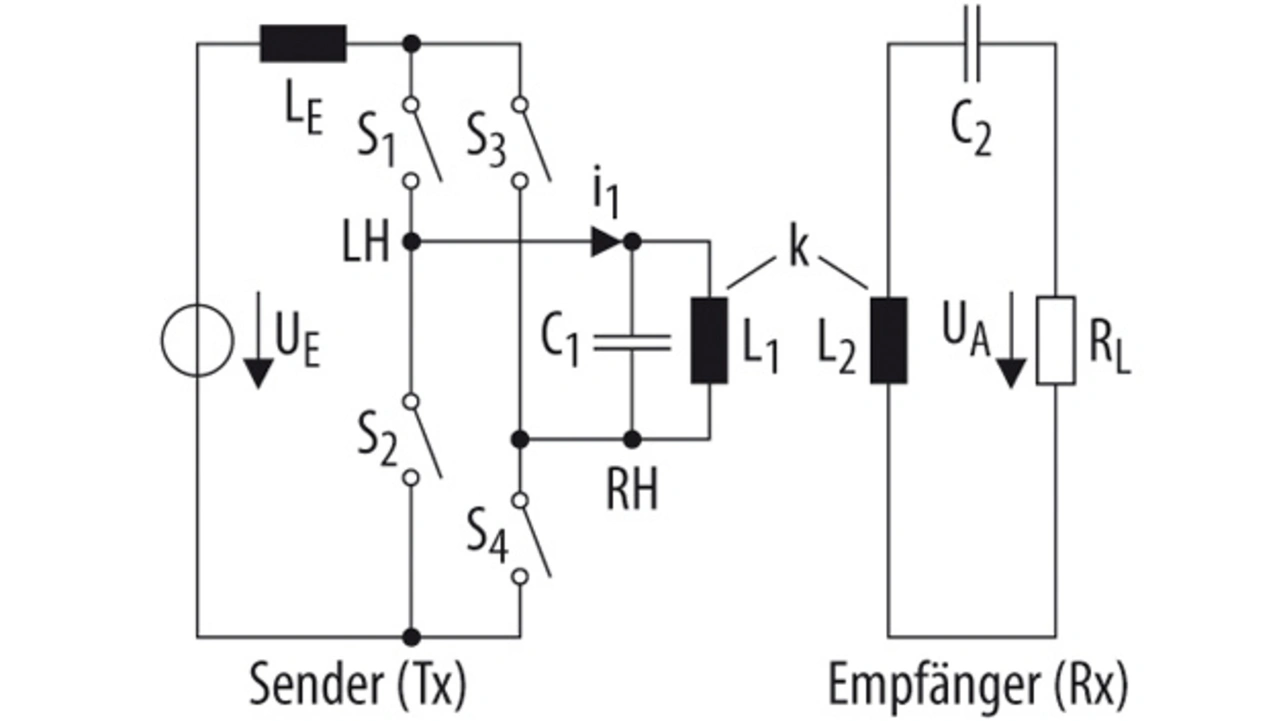
Mit der in Bild 4 gezeigten Parallelresonanz-Schaltung, gespeist aus einer Stromquelle, lassen sich die nicht funktionsbezogenen Anforderungen möglicherweise besser erfüllen. Mit Modifikationen an der Senderseite wird nachfolgend versucht, sowohl die funktionsbezogenen als auch die nicht funktionsbezogenen Anforderungen zu erfüllen.

Die Drossel L_E wird an der Gleichspannungsseite der Wechselrichterstufe angeordnet, um eine Stromquelle zu realisieren, die den parallelresonanten, induktiven Koppler speist. Zur Analyse der Eigenschaften dieser Schaltung können mathematische Analysen sowie Simulationen im Zeit- und Frequenzbereich durchgeführt werden. Es zeigt sich, dass das Vorhandensein von L_E die Simulationen der Schaltung im Frequenzbereich erschwert. Mithilfe geeigneter mathematischer Analysen lässt sich die Schaltung jedoch so reduzieren, dass die weitere Evaluierung fortgesetzt werden kann. Hierfür werden die folgenden realistischen Werte gewählt:

f_Tx = f_Rx = 33 kHz
L₁ = 290 µH
L₂ = 290 µH
C₁ = 1/(4 π² f_Rx² L_r)
C₂ = 1/(4 π²f_Rx² L₂)
L_E = 1 mH
L_r = L₁||2 L_E
k = 0,35
R_L = 10 Ω
U_E = 325 V (DC) im Zeitbereich

Analyse der stromgespeisten Parallelresonanz-Schaltung

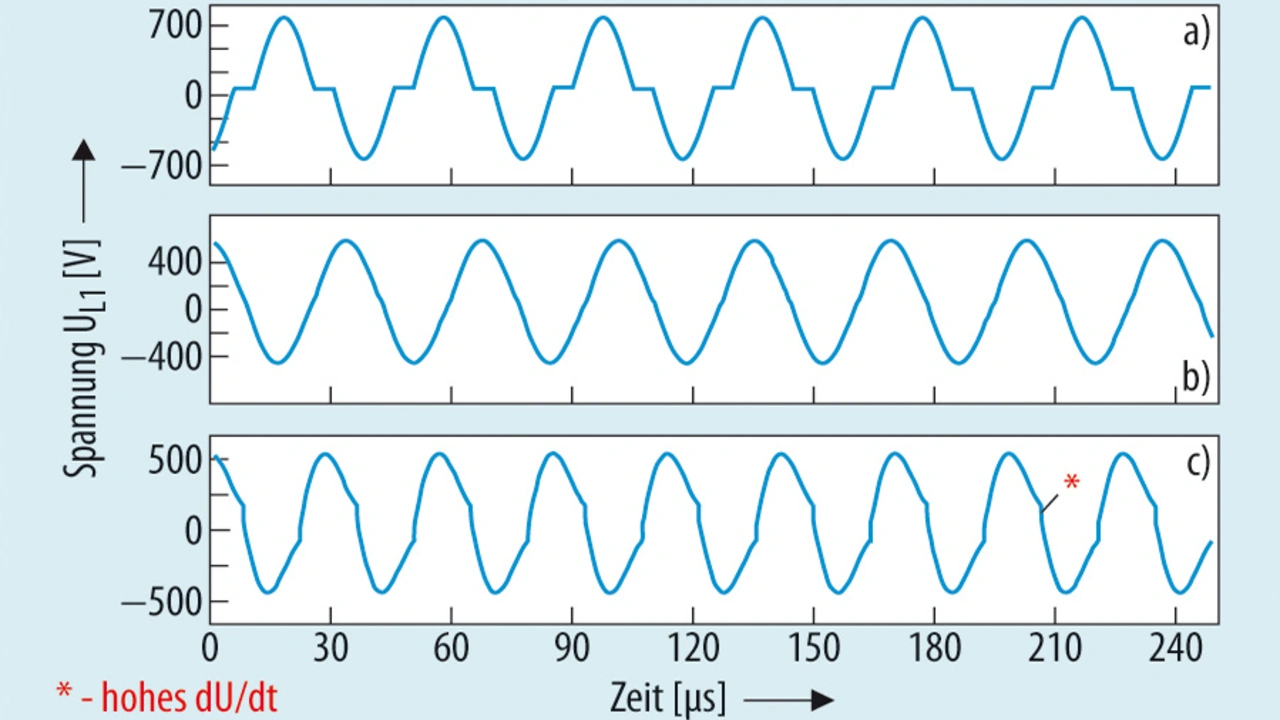
Die beschriebene Schaltung beruht auf dem Prinzip der Parallelresonanz, wobei die Schaltung bei den Resonanzfrequenzen eine maximale Impedanz aufweist. Bei dieser Schaltung und den verwendeten Bauteilwerten ergibt sich für das Gesamtsystem eine Resonanzfrequenz f_r1 von 28,2 kHz. Mithilfe der errechneten Werte für die Schaltungskomponenten lässt sich die Schaltung (Bild 4) im Zeitbereich simulieren.

Bild 5 gibt die Spannung an der Sendespule des resonanten induktiven Kopplers wieder, wenn die Wechselrichterstufe mit einer Fequenz f < f_r1, f = f_r1 bzw. f > f_r1betrieben wird. Interessanterweise ist aus Bild 5 zu entnehmen, dass keine steilen Spannungsflanken zu beobachten sind, wenn der Sender bei f_r1 oder unterhalb von f_r1 betrieben wird.

Um die im vorigen Abschnitt formulierten Anforderungen zu erfüllen, ist es deshalb vorzuziehen, diese Schaltung mit f_r1 oder einer niedrigeren Frequenz arbeiten zu lassen.

Arbeitet das Wireless-Power-System mit einer Frequenz unterhalb f_r1, hat die Spannung in der Sendespule einen nahezu sinusförmigen Verlauf. Eine Abweichung besteht nahe des Nulldurchgangs der Sinuswelle, wenn die Spannung für eine Zeitspanne (T_Null) nahezu null ist.

Für die Untersuchung der mit f_r1 oder einer niedrigeren Frequenz arbeitenden Schaltung kann daher mit der Grundschwingungsanalyse (FHA – First Harmonic Approximation) erfolgen [3]. Mithilfe dieser Methode lässt sich eine vereinfachte Ersatzschaltung herleiten (Bild 6). Darin steht R₁ für den effektiven Serienwiderstand der Sendespule (L₁), den effektiven Serienwiderstand der Drosselspule (L_E) und den effektiven Serienwiderstand des Kondensators (C₁).

R₂ repräsentiert den effektiven Serienwiderstand der Empfangsspule (L₂) und den effektiven Serienwiderstand des Kondensators (C₂). U₁₂ entspricht der Spannung, die durch die Gegeninduktivität (M) und den in der Empfangsspule fließenden Strom (I₂) in der Sendespule induziert wird.

Die Grundschwingungsanalyse ermöglicht es, die Stromquelle (I_AC) und den Kondensator (C₁) durch eine Wechselspannungsquelle (Û_AC) zu ersetzen. Der Kondensator C₁ in der Senderschaltung hat keinen Einfluss auf die Spannungsverstärkung des Empfängers, wohl aber auf die Phasenlage des Eingangsstroms (I₁). C1 kann daher als Phasenkompensator für den aus der Wechselspannungsquelle (Û_AC) aufgenommenen Eingangsstrom betrachtet werden.

Normalisierte Grundschwingungsanalyse

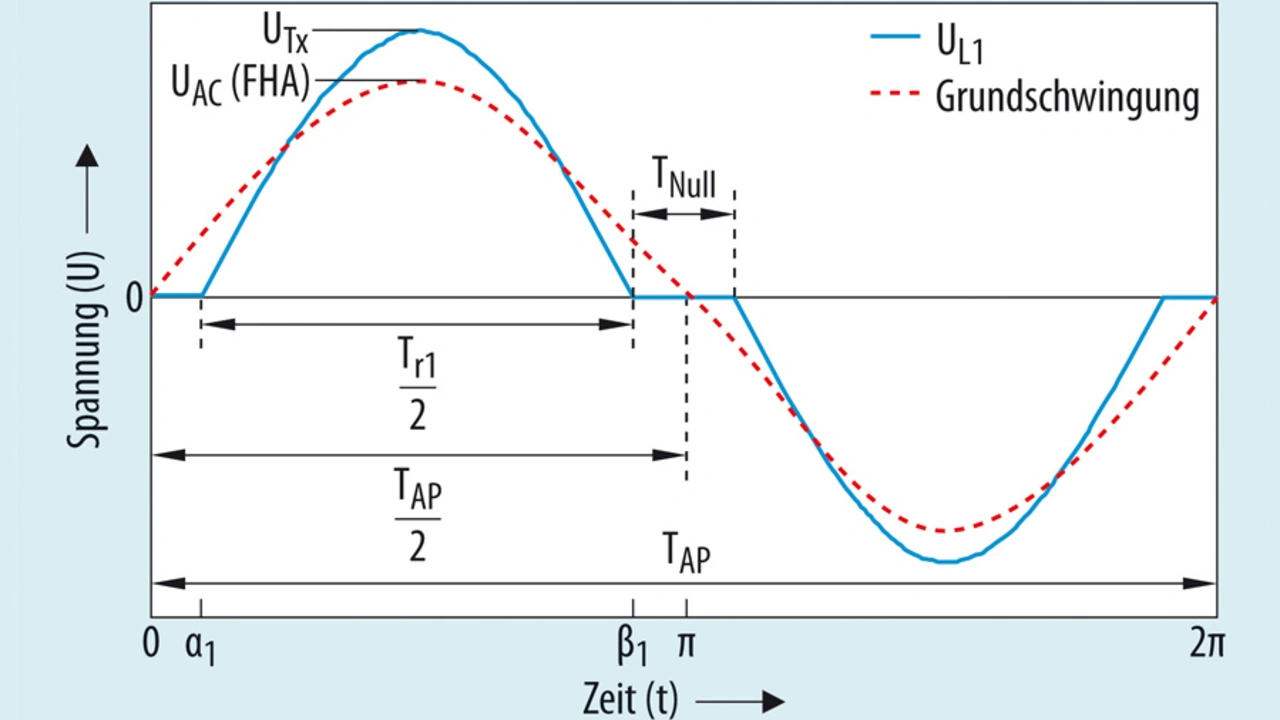
Wenn die Wechselrichterstufe des Senders unterhalb von f_r1 betrieben wird, scheint der Spannungsverlauf an der Sendespule eine unstetige Funktion zu sein, wie Bild 5a zeigt. Mithilfe von Simulationen im Zeitbereich lässt sich beobachten, dass der Spitzenwert der Spannung an der Sendespule (U_Tx) und die Zeitspanne mit 0 V (T_Null) umso höher wird, je weiter die Betriebsfrequenz abgesenkt wird. Hieraus lässt sich die Aussage herleiten, dass sich die Amplitude der ersten Harmonischen ebenfalls mit der Betriebsfrequenz f ändert.

Folglich ist es vergleichsweise schwierig, Simulationen im Frequenzbereich mit der in Bild 6 gezeigten Ersatzschaltung anzustellen. Um mit den Simulationen im Frequenzbereich bessere Ergebnisse zu erzielen, muss die Quelle (Û_AC) so modelliert werden, dass sich die Amplitude der ersten Harmonischen entsprechend der Betriebsfrequenz ändert.

Die Beziehung zwischen der Amplitude der ersten Harmonischen und der Betriebsfrequenz lässt sich mit einer Fourier-Analyse des Spannungsverlaufs an der Sendespule (Bild 7) herleiten. Aus Bild 8 wiederum kann der Zusammenhang zwischen der Maximalamplitude (U_Tx) und der Betriebsfrequenz (f_AP) hergeleitet werden. Dazu die folgende Gleichung:

U_Tx = f(f_AP, f_r) (1)

Bei f_AP = f_r beträgt die Maximalamplitude:

U_Tx,r =(U_E × π)/2 (2)

Mithilfe von Gleichung 1 lässt sich die Amplitude der ersten Harmonischen (U_AC) wie folgt ausdrücken:

U_AC,FHA = f(U_Tx, f_AP, f_r) (3)

Û_AC = (U_AC,FHA / U_Tx,f) (4)

Der normalisierte Wert (Û_AC) kann in Bild 6 für Simulationen im Frequenzbereich verwendet werden. Anzumerken ist, dass die Grundschwingungsanalyse nur bei oder unterhalb von f_r1 angewendet werden kann. Das gesamte mathematische Modell für die Analyse im Frequenzbereich ist deshalb nur bei oder unterhalb von f_r1 gültig.