Stromversorgung
Digitale stromgeführte Spitzenwertregelung von DC/DC-Wandlern
Fortsetzung des Artikels von Teil 4
Berechnungsbeispiel
Die am Beispiel eines Abwärtswandlers (Tabelle) mit stromgeführter, digitaler Spitzenwertregelung gezeigten Entwurfsprinzipien können mit geringfügigen Modifikationen auch für andere Wandlerschaltungen angewendet werden.
| Parameter | Wert |
|---|---|
| Eingangsspannung (UE) | 12 V |
| Ausgangsspannung (UA) | 3,3 V |
| Ausgangsstromstärke (IA) | 2 A |
| Lastwiderstand (RL) | 1,65 Ω |
| Induktivität (LA) | 22 µH |
| Ausgangskondensator (CA) | 440 µF |
| Ersatzreihenwiderstand (ESRCA) | 31 mΩ |
| Verstärkungsfaktor des Stromwandlers (Ri) | 0,48 |
| Tastverhältnis (TV) | 0,275 |
| Schaltfrequenz (fS) | 200 kHz |
| Durchtrittsfrequenz (fX) | 10 kHz |
Tabellarisch die technischen Daten des im Entwurfsbeispiel gewählten digital geregelten DC/DC-Wandlers.
Schritt 1: Berechnen der Höhe für die Kompensation des Stromanstiegs
Anhand Gleichung (2) wird der Spitze-Spitze-Wert der externen Stromanstiegs-Kompensation berechnet, der erforderlich ist, um Q = 1 zu erreichen:

Schritt 2: Berechnen der Positionen der Pole und Nullstellen für die analoge Kompensation
Bei diesem Abwärtswandler wird eine Kompensationsschaltung 2. Ordnung verwendet, mit der Übertragungsfunktion aus Gleichung 7. Die Polstelle ωP1 wird zum Aufheben der ESR-Nullstelle des Ausgangskondensators und des Ersatzserienwiderstands (ESR) verwendet:

Die Nullstelle der Kompensationsschaltung wird dazu verwendet, die Phasenreserve des offenen Regelkreises bei der Durchtrittsfrequenz festzulegen. Eine Näherung, die akzeptable Ergebnisse liefert: Die Nullstelle wird auf ein Fünftel der Durchtrittsfrequenz gelegt.

Zu guter Letzt wird anhand von Gleichung (10) der Pol am Ursprung - bzw. die Verstärkung der Kompensationsschaltung - berechnet, um die gewünschte Durchtrittsfrequenz ωP0 zu ermitteln:

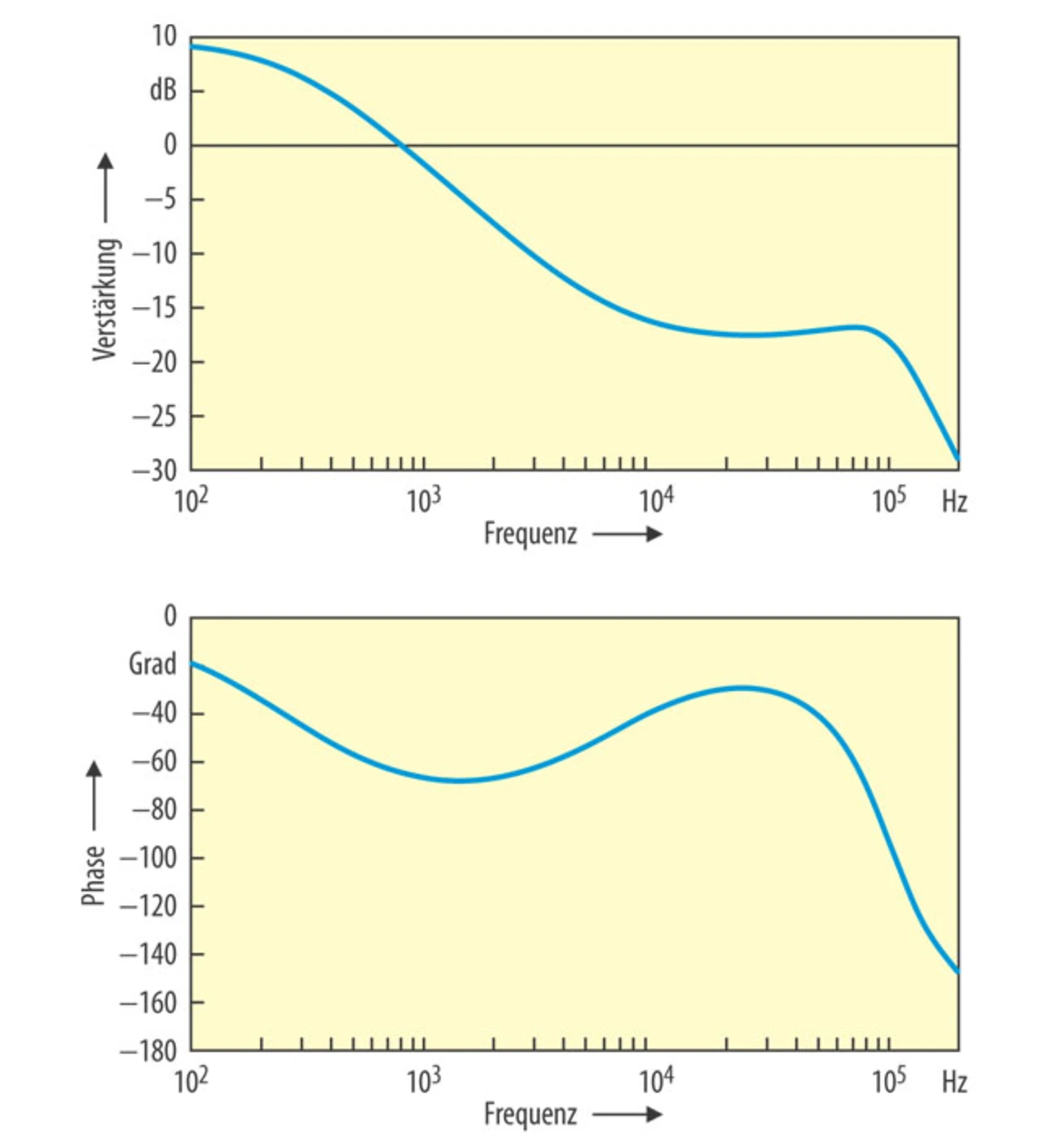
In Bild 6 ist der Frequenz- und Phasengang des DC/DC-Wandlers dargestellt - d.h. die Übertragungsfunktion vom Reglereingang zum Ausgang. Hier ist die doppelte Polstelle bei halber Schaltfrequenz deutlich zu sehen. Die gewählte Kompensationsschaltung hat die Resonanzüberhöhung dieser doppelten Polstelle deutlich gedämpft.
Der Frequenzgang der Kompensationsschaltung ist in Bild 7 (grüne Linie) dargestellt. Die blaue Linie in Bild 7 stellt die kombinierte Übertragungsfunktion des Regelkreises dar. Dies ist der Frequenzgang des offenen Regelkreises. Die Verstärkungs- und Phasenreserve des Reglers und somit die relative Stabilität werden vom Verlauf dieser Linie bestimmt.
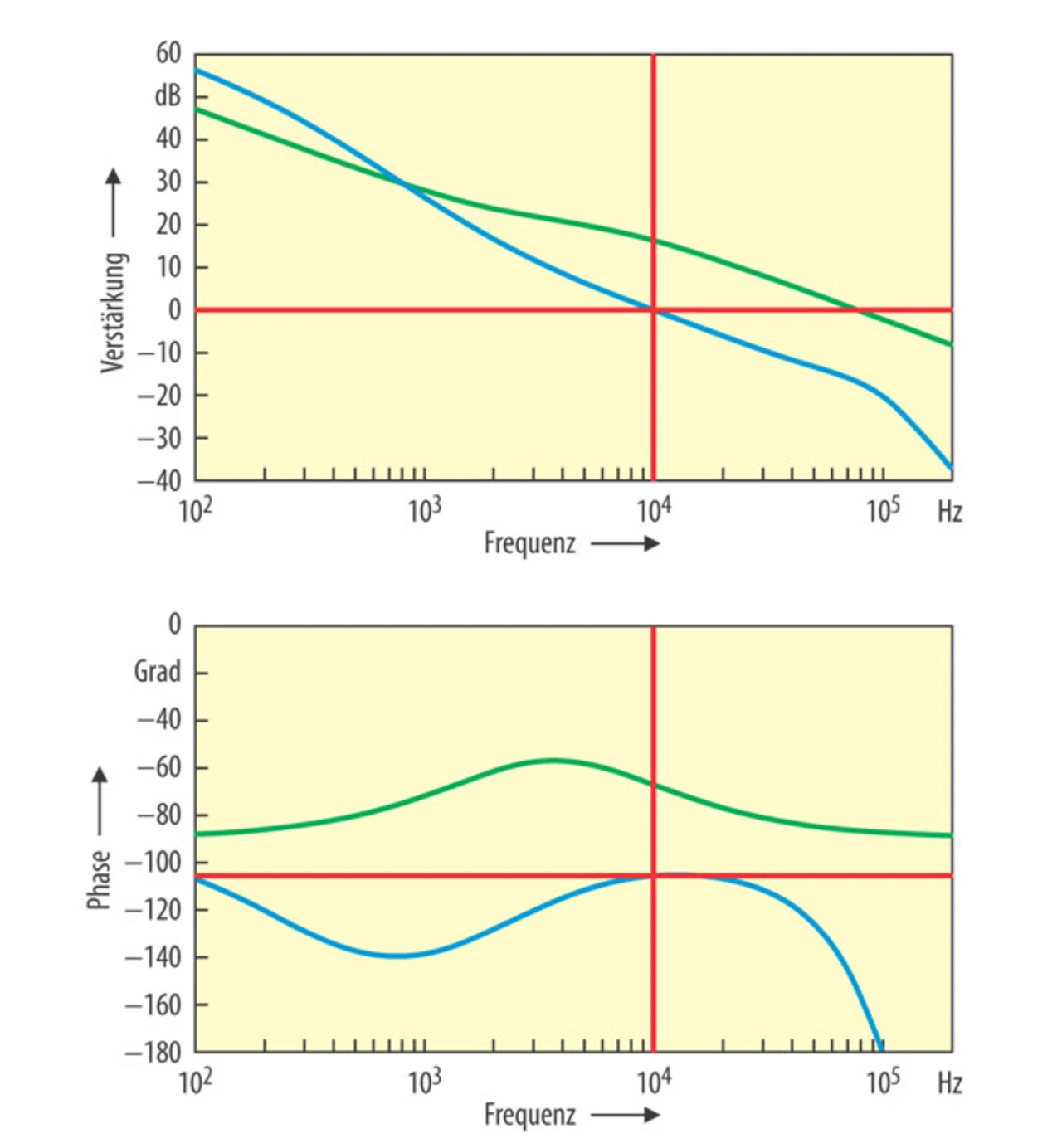
Der Regler ist für eine hohe Phasenreserve bei der Durchtrittsfrequenz von 10 kHz ausgelegt. Das Bode-Diagramm (Bild 7) des offenen Regelkreises zeigt, dass bei der Durchtrittsfrequenz eine Phasenreserve von 74,5° erreicht wird.
Schritt 3: Übertragen der analogen Kompensation in Digitalwerte
Zum Konvertieren in den Digitalbereich wird die bilineare Transformation verwendet. Sie kann automatisch mit einem Online-Hilfsprogramm ausgeführt werden [6]. Dazu müssen die folgenden Informationen in das Online-Formular eingegeben werden:
Durchtrittsfrequenz der Polstelle:
 kHz«/mi»«mo»§nbsp;«/mo»«mo»§nbsp;«/mo»«mo»(«/mo»«mn»21«/mn»«mo»)«/mo»«/math»" align="middle">
kHz«/mi»«mo»§nbsp;«/mo»«mo»§nbsp;«/mo»«mo»(«/mo»«mn»21«/mn»«mo»)«/mo»«/math»" align="middle">
Frequenz der zweiten Polstelle:

Frequenz der ersten Nullstelle:

Schaltfrequenz: fs = 200 kHz
Das Online-Hilfsprogramm liefert als Ergebnis die Koeffizienten der Übertragungsfunktion entsprechend der Formel
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»H«/mi»«mfenced close=¨]¨ open=¨[¨»«mi»z«/mi»«/mfenced»«mo»=«/mo»«mfrac»«mrow»«mi»U«/mi»«mfenced close=¨]¨ open=¨[¨»«mi»z«/mi»«/mfenced»«/mrow»«mrow»«mi»E«/mi»«mfenced close=¨]¨ open=¨[¨»«mi»z«/mi»«/mfenced»«/mrow»«/mfrac»«mo»=«/mo»«mfrac»«mrow»«msub»«mi»B«/mi»«mn»2«/mn»«/msub»«msup»«mi»z«/mi»«mrow»«mo»-«/mo»«mn»2«/mn»«/mrow»«/msup»«mo»+«/mo»«msub»«mi»B«/mi»«mn»1«/mn»«/msub»«msup»«mi»z«/mi»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/msup»«mo»+«/mo»«msub»«mi»B«/mi»«mn»0«/mn»«/msub»«/mrow»«mrow»«mo»-«/mo»«msub»«mi»A«/mi»«mn»2«/mn»«/msub»«msup»«mi»z«/mi»«mrow»«mo»-«/mo»«mn»2«/mn»«/mrow»«/msup»«mo»-«/mo»«msub»«mi»A«/mi»«mn»1«/mn»«/msub»«msup»«mi»z«/mi»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/msup»«mo»+«/mo»«mn»1«/mn»«/mrow»«/mfrac»«mo»§nbsp;«/mo»«mo»§nbsp;«/mo»«mo»(«/mo»«mn»24«/mn»«mo»)«/mo»«/math»](/js/tinymce/jscripts/tiny_mce/plugins/tiny_mce_wiris/integration/showimage.php?formula=e70efc165a106d076409e5f4018d5253.png)
Die so erhaltenen Koeffizienten
A1 = 1,69021065681
A2 = -0,6902106568
B0 = 2,0654678327
B1 = 0,1258242849
B2 = -1,9396435478
muss der Entwickler dann nur noch in der Gleichung für den Regler mit zwei Pol- und zwei Nullstellen verwenden. Die CSL-Programmierumgebung bietet für diesen Regler eine dedizierte Funktion.
Schritt 4: Initialisieren
Sowohl bei der Programmierumgebung von Biricha Digital Power (CSL) als auch bei der Controlsuite von Texas Instruments werden die Parameter für den digitalen, stromgeführten Regler am Anfang der C-Datei als #define-Anweisung eingegeben.
Für die Berechnung des digitalen Fehlerwertes wird eine Referenz verwendet, wobei der Wert des A/D-Umsetzer-Ausgangs von der Referenz subtrahiert wird. Der digitale Fehlerwert dient dann als Eingangswert für den Regler.
Daher muss der Referenzwert gleich dem digitalen Äquivalent der Ausgangsspannung multipliziert mit der Verstärkung der Abtast-/Spannungsteiler-Schaltung sein.

Für den 3,3-V-Ausgang mit einer Verstärkung von 0,5 der Abtast-/Spannungsteiler-Schaltung und einem 12-bit-A/D-Umsetzer ergibt sich somit

Der Regler mit zwei Pol- und zwei Nullstellen kann nun am Anfang der C-Datei konfiguriert werden:
/* Einrichten der Koeffizienten für den Regler mit zwei Pol- und zwei Nullstellen */
#define REF (_IQ15toF(2048))
#define MIN_DUTY 0
#define MAX_DUTY 65535
#define A1 +1.6902106568
#define A2 -0.6902106568
#define B0 +2.0654678327
#define B1 +0.1258242849
#define B2 -1.9396435478
#define PERIOD_NS 5000 /* Periodendauer in ns für fs = 200 kHz */
Der letzte Term, der nun noch berechnet werden muss, ist der Verstärkungsfaktor K. Damit sollen die Auswirkungen der diversen Verstärkungen im Mikrocontroller aufgehoben werden, um die richtige Durchtrittsfrequenz zu erreichen. Der Wert für K lässt sich genau berechnen. Jedoch würde eine Beschreibung der entsprechenden Vorgehensweise den Rahmen dieses Aufsatzes sprengen.
Der Verstärkungsfaktor K lässt sich aber auch sehr einfach messtechnisch ermitteln. Dazu wird ein Anfangswert definiert - in diesem Beispiel wird ein Anfangswert von K = 10 gewählt. Damit wird die Regler-Software implementiert und anschließend der Regelkreis mit einem Netzwerkanalysator wie z.B. dem Bode-100 von Omicron Lab untersucht. Nun wird der Wert für K in der Software so angepasst, dass die richtige Durchtrittsfrequenz erreicht wird.
Die Programmierung und die Implementierung des Programmcodes, incl. Listings, sowie die messtechnische Ermittlung des Verstärkungsfaktors K sind im zweiten Teil des Aufsatzes veröffentlicht.
- Digitale stromgeführte Spitzenwertregelung von DC/DC-Wandlern
- Modell für die stromgeführte Spitzenwertregelung
- Entwerfen digitaler Regler
- Digitale Stromanstiegskompensation
- Berechnungsbeispiel
- Literatur & Autor





