Digitale stromgeführte Spitzenwertregelung von DC/DC-Wandlern

Modell für die stromgeführte Spitzenwertregelung

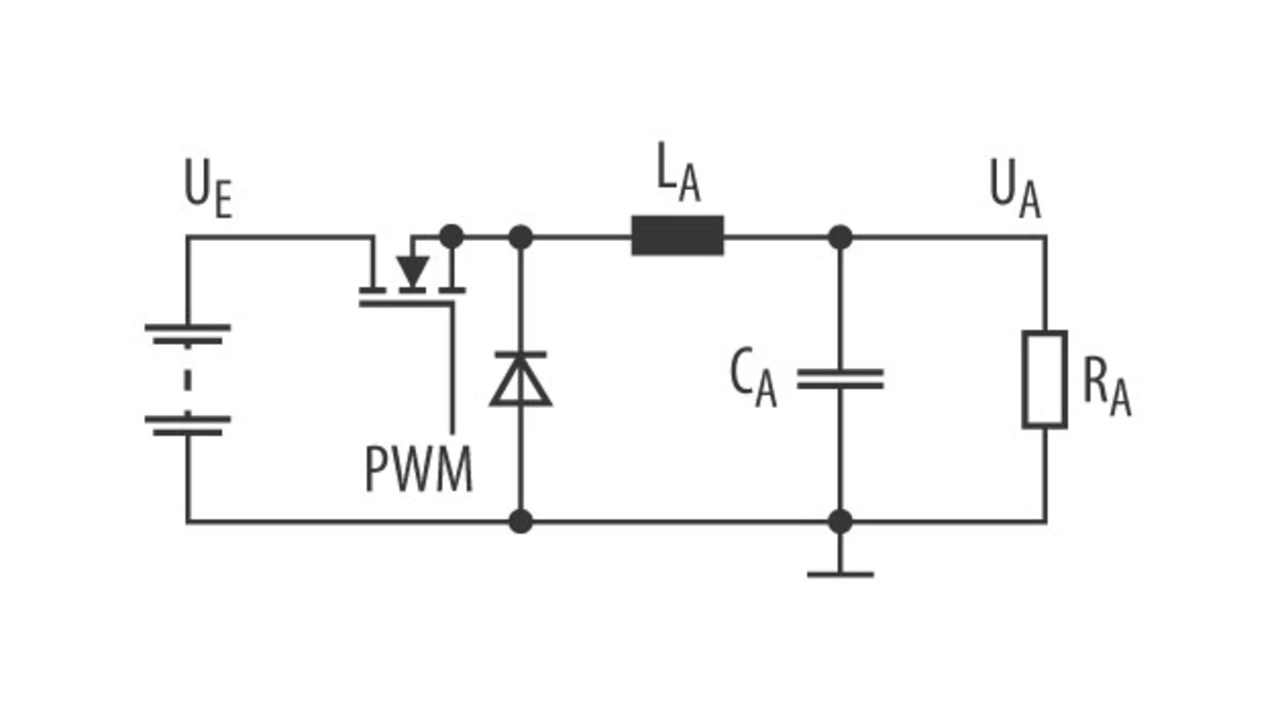
Der in Bild 3 vereinfacht dargestellte Abwärtswandler dient zur Veranschaulichung der stromgeführten Spitzenwertregelung. Die Vorgehensweise kann jedoch auch bei anderen Schaltungen angewendet werden. Um eine stabil arbeitende Kompensationsschaltung zu entwerfen, wird zuerst ein mathematisches Modell der Abwärtswandlerschaltung benötigt. Gemäß [1] kann eine Abwärtswandlerschaltung mit drei Termen beschrieben werden, nämlich

F_H(s), der Hochfrequenz-Übertragungsfunktion,
H_DC, der Gleichstromverstärkung und
H_B(s), dem Kleinsignalverhalten der Leistungsstufe.

Die vollständige Übertragungsfunktion des Reglers für einen Abwärtswandler mit stromgeführter Spitzenwertregelung [2] ist eine Kombination dieser drei Terme:

Hochfrequenz-Übertragungsfunktion

Die Hochfrequenz-Übertragungsfunktion F_H(s) weist eine doppelte Polstelle bei halber Schaltfrequenz (f_S) auf. Dies führt unweigerlich zu einer Resonanzüberhöhung bei dieser Frequenz, die gedämpft werden muss. Um Instabilität zu verhindern, darf die Verstärkungskennlinie im Bode-Diagramm bei der Resonanzfrequenz die 0-dB-Achse nicht überschreiten.

Dazu wird dem Regelkreis eine Stromanstiegs-Kompensation hinzugefügt, um die Resonanzüberhöhung effektiv zu dämpfen. Dies wird erreicht, indem die Güte (Q) des Reglers auf 1 gesetzt wird. Bei niedriger Güte wird die Resonanzüberhöhung gedämpft und die Verstärkung bei f_S/2 verringert.

Der für einen Abwärtswandler erforderliche Spitze-Spitze-Wert der externen Stromanstiegs-Kompensation wurde in [3] berechnet und ist in Gleichung (2) dargestellt. Die Stromanstiegs-Kompensation verringert die Güte der Hochfrequenz-Übertragungsfunktion auf 1.

wobei R_i = Verstärkung des Stromwandlers,
T_S = Periodendauer der Schaltfrequenz,
U_E = Eingangsspannung,
L_A = Ausgangsspule und
TV = U_A/U_E = Tastverhältnis mit
U_A = Ausgangsspannung

Mit einer Güte von 1 kann F_H(s) vereinfacht werden zu

mit ω_N = ½ω_S = ½ × 2πf_S

Gleichstromverstärkung

Mit dem Modell von Ridley [2] und der Dämpfung der Resonanzüberhöhung durch Setzen der Güte auf 1 kann die Gleichstromverstärkung des Reglers vereinfacht werden zu

mit R_A = Lastwiderstand am Ausgang.

Kleinsignalverhalten  der Leistungsstufe

Aufgrund der stromgeführten Regelung wird die Spule des Abwärtswandlers in Bild 1 zu einer stromgeregelten Quelle. In [1] wird das Kleinsignalverhalten des Abwärtswandlers angegeben als

Die Polstelle ω_OP wird von der Ausgangskapazität und dem Lastwiderstand bestimmt. Mit einer Güte von 1 kann die Polstelle ω_OP anhand der Gleichung (6) berechnet werden:

Des Weiteren wird die Nullstelle ω_ESR von der Ausgangskapazität und dem äquivalenten Serienwiderstand (ESR) des Ausgangskondensators C_A festgelegt gemäß

Pol- und Nullstellen der Kompensation

Die Pol- und Nullstellen der Kompensationsschaltung können nun, gemäß der Analyse der Übertragungsfunktion von der Regelung bis zum Ausgang, so gewählt werden, dass die gewünschte Durchtrittsfrequenz und Phasenreserve des Reglers erreicht wird. Für die Kompensation des Abwärtswandlers mit stromgeführter Spitzenwertregelung wird ein Netzwerk 2. Ordnung verwendet. Die Übertragungsfunktion hierfür lautet

Die Polstelle ω_P2 der Kompensationsschaltung wird auf die Frequenz der ESR-Nullstelle (ω_ESR) in der Übertragungsfunktion (Formel 7) gelegt, um deren Auswirkungen näherungsweise aufzuheben (ω_P2 = ω_ESR). Die Nullstelle ω_Z1

mit f_X = Durchtrittsfrequenz

wird auf einen Wert gesetzt, mit dem eine geeignete Phasenreserve erreicht werden kann. Die Polstelle am Ursprung, ω_P0, wird auf einen Wert gesetzt, mit dem sich eine geeignete Durchtrittsfrequenz erreichen lässt. Die Frequenz der Nullstelle des Kompensationsnetzwerkes sollte auf 20 % der gewünschten Durchtrittsfrequenz gelegt werden. In den meisten Fällen führt dies zu einer angemessenen Phasenreserve.

Zu guter Letzt wird die Polstelle am Ursprung - bzw. die Verstärkung des Kompensationsnetzwerkes - berechnet. Dabei handelt es sich um die Frequenz, bei der die Verstärkung einzig aufgrund der Polstelle am Ursprung 1 betragen würde. Diese Frequenz wird als Durchtrittsfrequenz f_X gewählt.

Aus der Übertragungsfunktion des Abwärtswandlers (Formel 1) wurde Gleichung (10) abgeleitet, um ω_P0 des Kompensators direkt berechnen zu können [2]:

mit

Mit diesen Formeln lässt sich allerdings nur eine Annäherung berechnen. Die exakte, analytische Berechnung der Null- und der Polstelle am Ursprung ist umfangreich und würde den Rahmen dieses Aufsatzes sprengen [4].

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

1. Digitale stromgeführte Spitzenwertregelung von DC/DC-Wandlern
2. Modell für die stromgeführte Spitzenwertregelung
3. Entwerfen digitaler Regler
4. Digitale Stromanstiegskompensation
5. Berechnungsbeispiel
6. Literatur & Autor

Lesen Sie mehr zum Thema

Das könnte Sie auch interessieren

Stromversorgung

Implementierung eines digitalen Schaltreglers

Weitere Artikel zu DC/DC-Wandler

Von Aufschwung kann noch keine Rede sein

Dt. Strom-Markt: Keine Katastrophe, aber viel Luft nach oben

Vishay entwickelt Lösungen

DC-Netze erobern die Welt

Microchip

Strahlungsgehärteter 15 W DC/DC-Wandler

»Zuverlässig, nachhaltig und flexibel«

50 Jahre Recom: Firmenmanagement im Wandel der Zeit

Gleichstrom für KI-Server

Nvidia und Infineon reduzieren KI-Strombedarf