Startseite > Halbleiter > Analog- / Mixed-Signal > Temperatur fernabfragen (Teil 2)

Powermanagment-IC auf Abwegen

Temperatur fernabfragen (Teil 2)

23. Oktober 2017, 13:00 Uhr | Ralf Higgelke

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 2

Quantisierung und Rauschen

Quantisierung

Im Allgemeinen ist die A/D-Wandlerabtastung mit zwei Arten von Abtastfehlern behaftet: Zeit- und Spannungsquantisierung, weil bei beiden Dimensionen das Signal jeweils nur diskrete Werte annehmen kann.

Eine typische Methode, die Ausgangsspannung eines A/D-Wandlers zu repräsentieren, ist es, den Signalwert plus etwas zusätzlichem Rauschen zu nehmen:

(19) $A D C minus C o d e open square brackets i close square brackets equals V e r s t ä r k u n g times open parentheses E i n g a n g s s p a n n u n g space plus e open square brackets i close square brackets close parentheses$
Wobei die Verstärkung 2N/U_{FULL_SCALE} und e[i] der Fehler in der Anzahl i der Abtastungen ist. Der Term e[i] für den Quantisierungsfehler repräsentiert den Spannungsunterschied zwischen der Eingangsspannung und der Spannung des am nächsten gelegenen A/D-Wandler-Codes. Dieser Fehler kann bis zu ±LSB/2 betragen, wenn die Eingangsspannung in der Mitte zwischen zwei benachbarten diskreten Codes des A/D-Wandlers liegt (Bild 11).

Bei einem rauschfreien DC-Eingang ist e[i] für alle Werte von i gleich. Alle Ausgangswerte des A/D-Wandlers sind dabei identisch und haben identische Fehler. Keine Nachbearbeitung kann diesen Fehler verringern. Nimmt man einen Durchschnitt von hundert Abtastungen, erhält man das gleiche Ergebnis wie bei nur einer einzigen Abtastung.

Rauschen

Wenn Rauschen auftritt, dann gibt es eine endliche Wahrscheinlichkeit, dass der A/D-Wandler einen anderen Code wählt, als im Fall ohne Rauschen. Wenn dieser Störfall eintritt, dann ist ADC-Code[i] ungleich ADC-Code[i-1] und das Mitteln mehrerer Abtastwerte des A/D-Wandlers kann eine genauere Angabe ergeben, da die Mittelung einen Teil des Quantisierungsfehlers eliminiert. Damit die Mittelung effektiv ist, muss das Rauschen über die Zeit dynamisch sein, nicht mit dem Eingang korreliert (echt zufällig) und eine symmetrische Verteilung um den Mittelwert Null haben. Sie sollte im Betrag auch größer sein als 1 LSB des A/D-Wandlers. Wenn dies so ist, dann kann das Mitteln einer ausreichend großen Anzahl von Abtastungen N den Rauschteppich auf unter 1 LSB des A/D-Wandlers reduzieren, sodass die gemittelte minimale Schrittgröße eintritt:

(20) $U subscript S t e p end subscript rightwards arrow U subscript L S B end subscript over N$

Ein solches Verhalten ist möglich, weil das Rauschen den Ausgang des A/D-Wandlers zum »Flattern« zwischen benachbarten Codes bringt, das Rauschen selbst aber einen Mittelwert von Null hat, sodass es aus der Mittelung heraus fällt. Der verbleibende Mittelwert ist genauer als der Wert der rauschfreien Messung.

Jobangebote+ passend zum Thema

Technischer Vertriebsmitarbeiter (m/w/d) für Industrie-PCs / Embedded Systeme

GLYN GmbH & Co. KG, Idstein

Quereinsteiger im Vertriebsinnendienst (m/w/d) für das Vertriebsbüro bei Wien

GLYN GmbH & Co. KG, Brunn am Gebirge

MACNICA ATD EUROPE - Ihre berufliche Zukunft

MACNICA ATD Europe GmbH, Ingolstadt

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

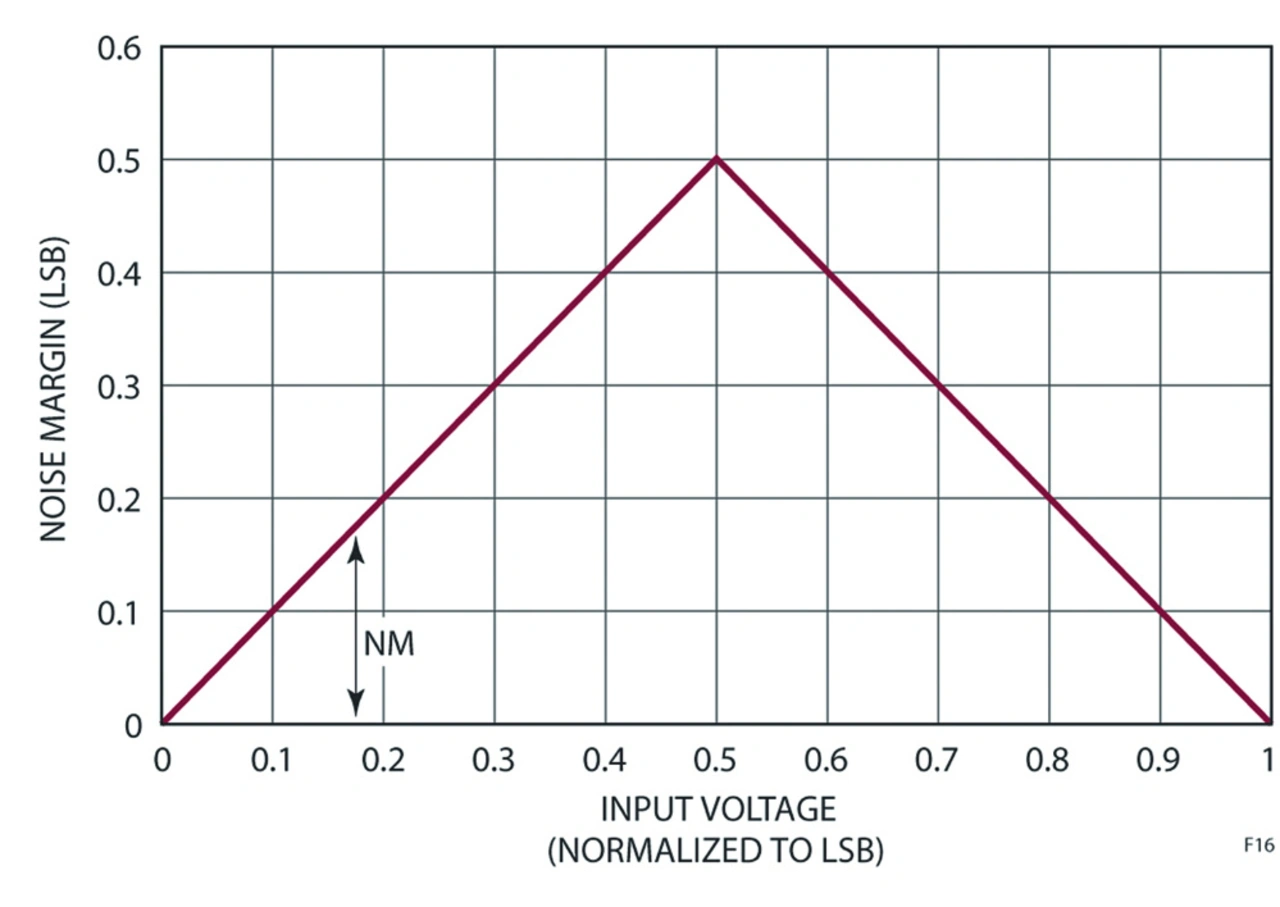
Um zu erkennen, warum das so ist, betrachten wir Bild 14. Der Rauschabstand auf der Y-Achse ist die Rauschgröße, die nötig ist, um den Ausgangswert bei einem gegebenen Eingangswert am A/D-Wandler auf der X-Achse zu verändern. Liegt der Eingang um LSB/2 neben der nächstgelegenen Schwellenspannung, dann ist ein Rauschen größer als LSB/2 nötig, um den Code zu ändern. Wenn die Eingangsspannung direkt auf dem Codeübergang liegt, dann veranlasst jegliches Rauschen, dass sich der Code ändert.

Wahrscheinlichkeit, dass Rauschen die Messung stört

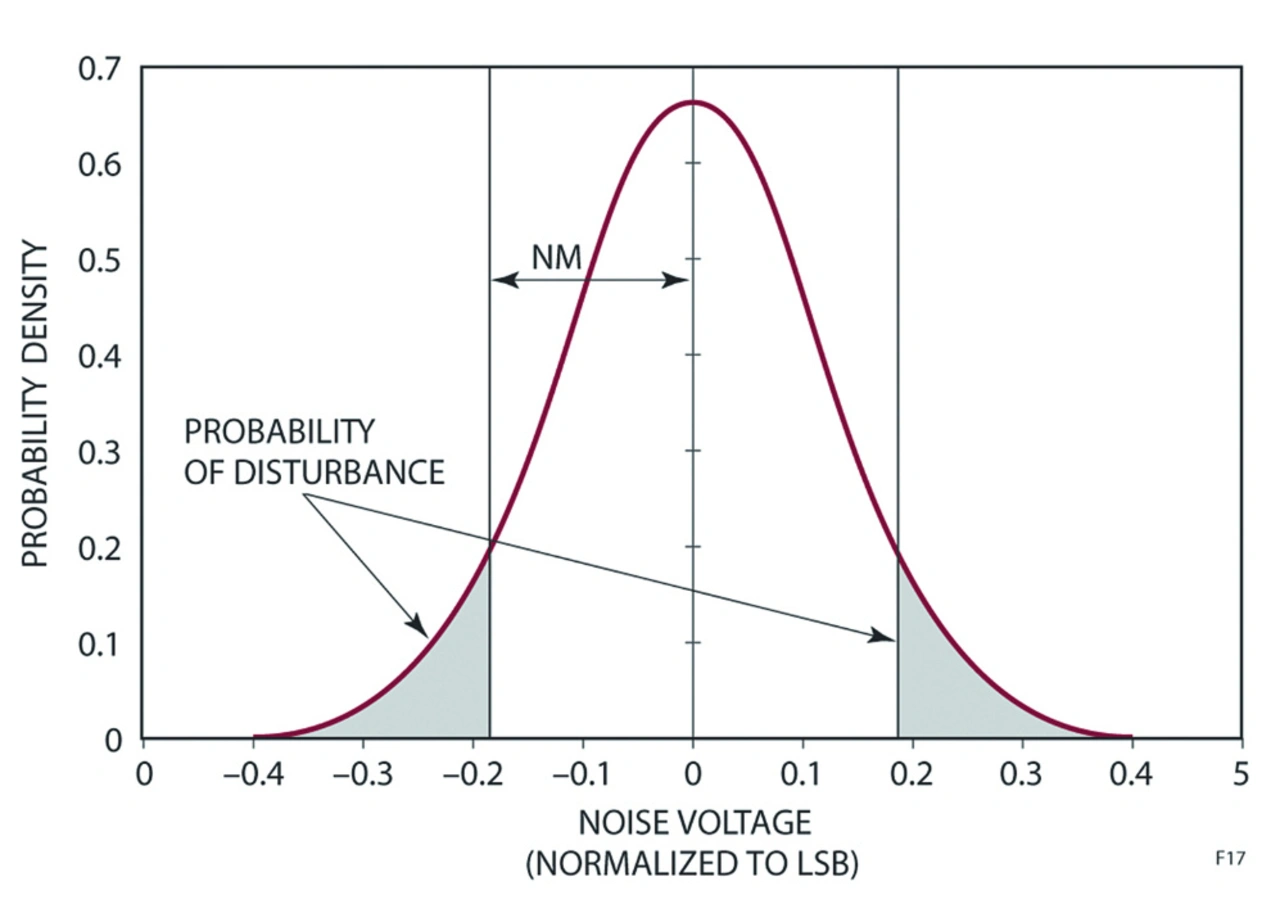
Man kann die Wahrscheinlichkeit berechnen, wann das Auftreten von Rauschen den A/D-Wandler veranlasst, seinen Ausgangswert zu ändern. Dazu lege man diesen Rauschabstand NM (Noise Margin) an die Wahrscheinlichkeitsdichtefunktion an (falls bekannt). Die Wahrscheinlichkeit einer Störung ist der integrierte Bereich unter der Kurve außerhalb des Fensters, definiert als μ + NM und μ – NM, wobei μ der Mittelwert ist (wahrscheinlich μ = 0, siehe Bild 15).

Durchläuft die Eingangsspannung des A/D-Wandlers einen Bereich, schwankt die Wahrscheinlichkeit, dass Rauschen die Messung stört, reproduzierbar hin und her. Nahe den Codeübergängen ist die Wahrscheinlichkeit hoch und nahe dem Zentrum des Codes ist die Wahrscheinlichkeit minimal. Man beachte, dass die präzise Form von der statistischen Verteilung des Rauschens abhängt. Hier ist zwar eine Gauß-Verteilung dargestellt, wahrscheinlicher aber ist, dass man wegen der diskreten Rauschfrequenzen eine multimodale Verteilung vorfinden wird.

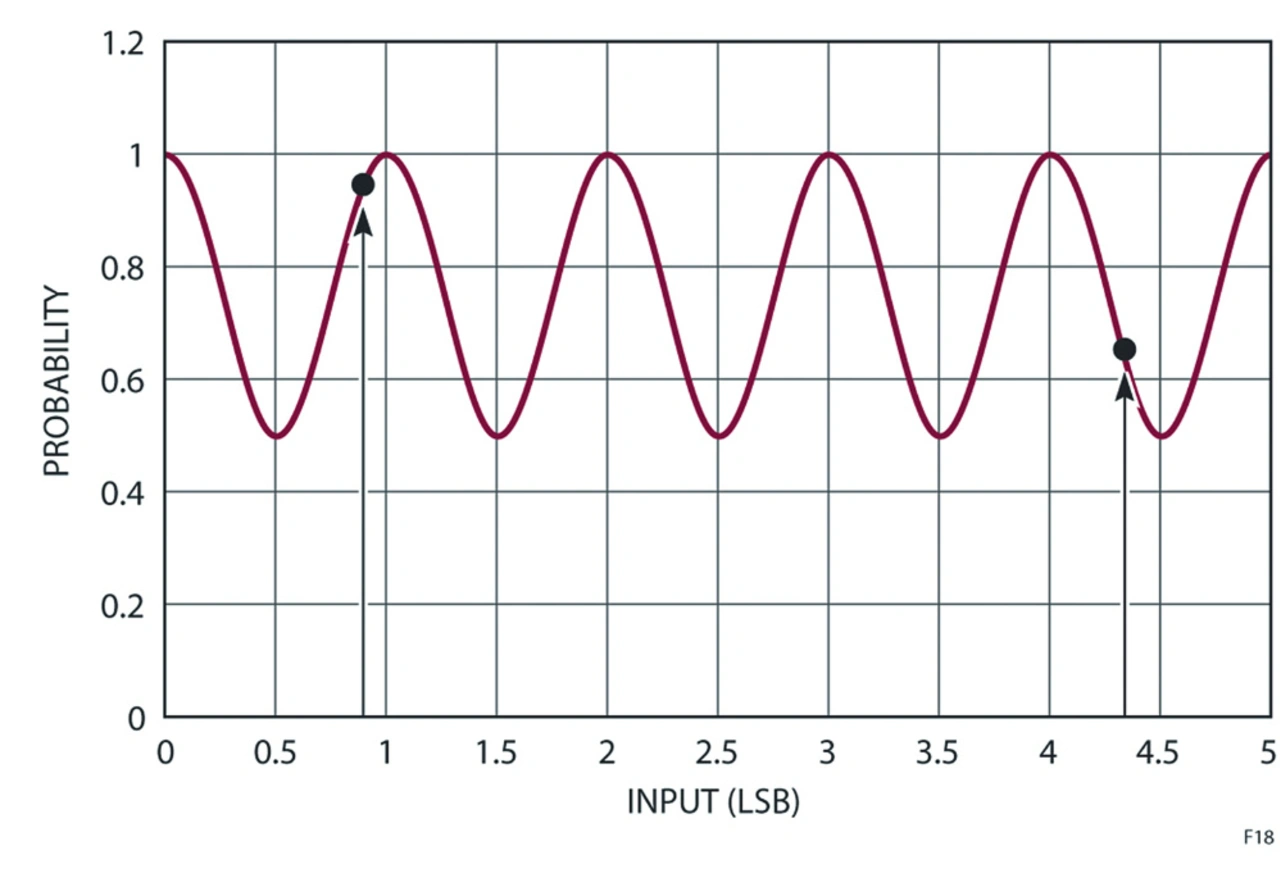
In jedem Fall bleibt die in Bild 16 dargestellte, wiederholte Art erhalten, selbst wenn ihre exakte Form unterschiedlich ist. Das Anlegen von zwei unterschiedlichen Eingangsspannungen an den A/D-Wandler (für Temperaturmessungen), ergibt zwei unterschiedliche Wahrscheinlichkeiten der Störung für den gemessenen Wert (die beiden Punkte in Bild 16). Da die Temperaturmessung aus mehreren Messungen des A/D-Wandlers zusammengesetzt ist, ist anzunehmen, dass manche Temperaturen empfindlicher als andere sind. Und da man die Temperaturen über einen Bereich durchlaufen lässt, ist jede einzelne Messung wiederum verrauscht, wenn sie ihren nächstgelegenen Schwellwert erreicht.

Im dritten und letzten Teil dieses Artikels wird es unter anderem um die Zeitquantisierung, Grenzen der Mittelwertbildung und das Aufdecken von Schaltungsfehlern gehen.