Powermanagment-IC auf Abwegen
Temperatur fernabfragen (Teil 2)
Fortsetzung des Artikels von Teil 1
Genauigkeit der Schaltung
Die Genauigkeit des Temperatursensors ist durch mehrere Faktoren begrenzt. Die fundamentale Gleichung (8) reagiert empfindlich auf die Werte des Nichtlinearitätsfaktors des Transistors, der gemessenen Spannung und des Stroms. Es gibt auch einige versteckte Nichtlinearitäten und Empfindlichkeiten, die nicht in Gleichung (8) erscheinen. Dies sind die Fehler in den Messungen des A/D-Wandlers – die integrale Nichtlinearität (INL), differenzielle Nichtlinearität (DNL), Verstärkung und Offset – und auch die nicht konstante Stromverstärkung des Transistors β.
Der A/D-Wandler hat mehrere Fehlerarten, die im Datenblatt aufgelistet sind. Dies sind Fehler in den gemessenen Werten, die durch die Unvollkommenheiten im A/D-Wandler entstehen.
- Verstärkung und Offset des A/D-Wandlers
Die Verstärkung des A/D-Wandlers ist idealerweise 1, das Datenblatt des LTC2970 zeigt jedoch, dass der Verstärkungsfehler weniger als 0,4 % beträgt – im schlechtesten Fall also 1,004. Für UBE-Messungen zwischen 574 mV und 640 mV (bei Raumtemperatur), wären die gemessenen Spannungen mit dem Verstärkungsfehler 576,30 mV bzw. 642,56 mV. Dadurch ändert sich ∆UBE von 66,0 mV auf 66,26 mV. Der Unterschied von 264 µV ist rund ein halbes LSB (500 µV), was einem Temperaturfehler von rund 1,2 K entspricht.
Der Offset des A/D-Wandlers ist faktisch ein fester Wert, der zu jedem Code hinzugefügt wird. Dies ist der Wert am Ausgang, wenn am Eingang eine Spannung von 0 V anliegt. Dies ist für die Temperaturberechnung die bei weitem empfindlichste Messung. Weil ∆UBE eine differenzielle Messung ist, werden Konstanten wie der Offset des A/D-Wandlers durch Subtrahieren eliminiert:
(14)
Offsets beeinflussen die ratiometrische Strommessung. Jedoch ist dieser Effekt gering, da die Empfindlichkeit auf das Verhältnis der Ströme klein ist.
Jobangebote+ passend zum Thema
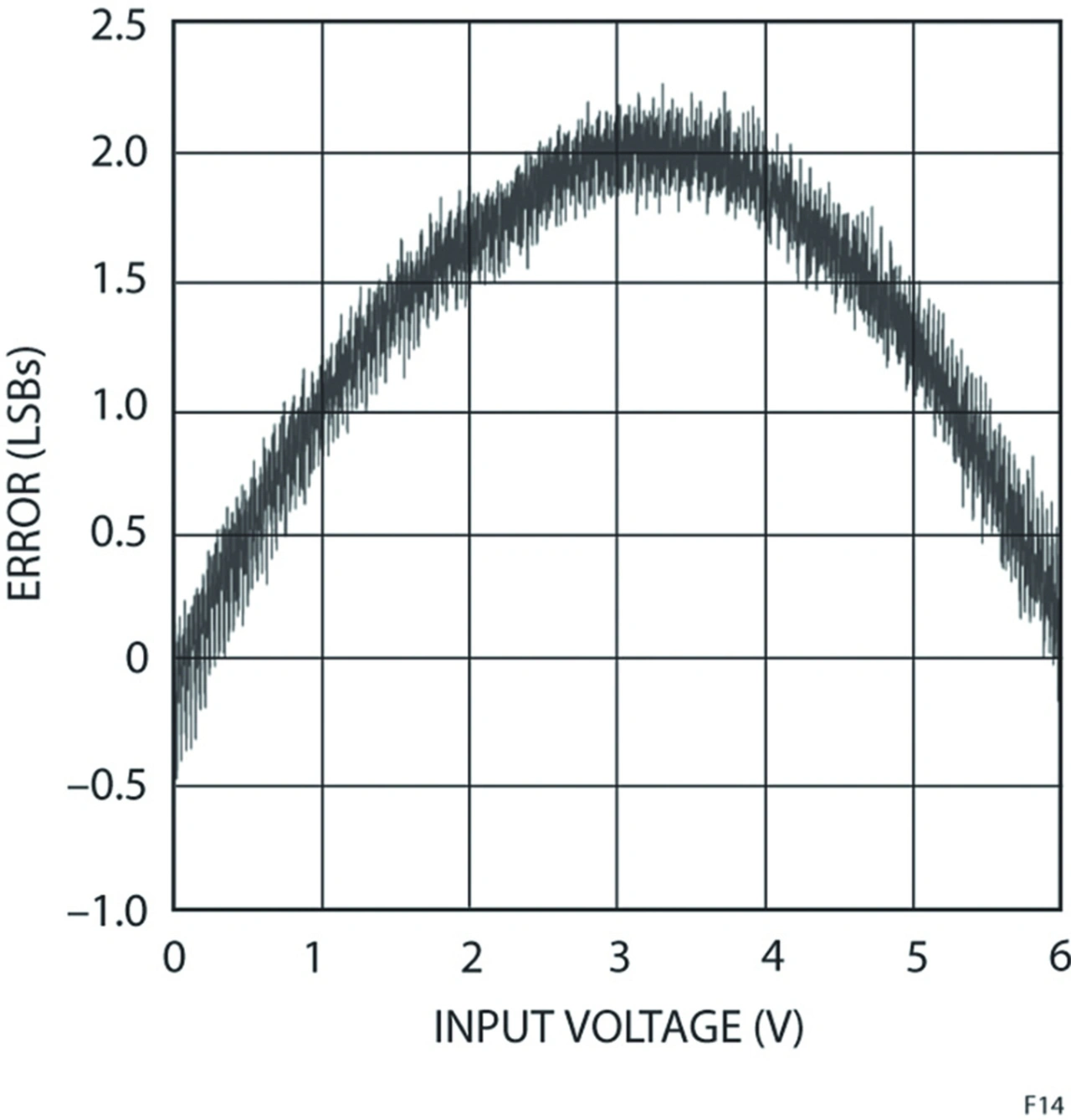
- INL und DNL des A/D-Wandlers
Das Datenblatt des LTC2970 zeigt die INL als Funktion der Eingangsspannung mit typischen Werten von 1 LSB für Spannungen nahe 1 V und der Annäherung an 0 LSB für Eingangsspannungen nahe 0 V. Dies impliziert, dass für ∆UBE-Messungen nahe 0,6 V ein INL-Fehler von etwa 0,6 LSB und eine Änderung von ungefähr 1 LSB/V bzw. 500 µV/V. Dies ist in Bild 12 gezeigt. Die INL-Kurve des A/D-Wandlers hat die gleiche Form für jedes Bauteil, sodass man die INL als einen Verstärkungsfehler behandeln kann mit einer um eine Größenordnung geringeren Effekt als der Verstärkungsfehler des A/D-Wandlers selbst. Damit sollten die Temperaturfehler unter 0,13 K bleiben.
- DNL des A/D-Wandlers
Das Datenblatt des LTC2970 spezifiziert die DNL (Schrittgrößenfehler von Codewort zu Codewort) unter 0,5 LSB oder 250 µV. Dies liegt in derselben Größenordnung wie der Verstärkungsfehler des A/D-Wandlers, sodass die Temperaturfehler unter 1,2 K liegen. Diese Fehler werden von zufälligen Fehlanpassungen verursacht und sind zugänglich für die Vermischung (Scrambling) mit einer Dithering-Quelle, die den angelegten Transistorstrom ändert. Dieser Fehler lässt sich durch eine anschließende Mittelwertbildung entfernen.
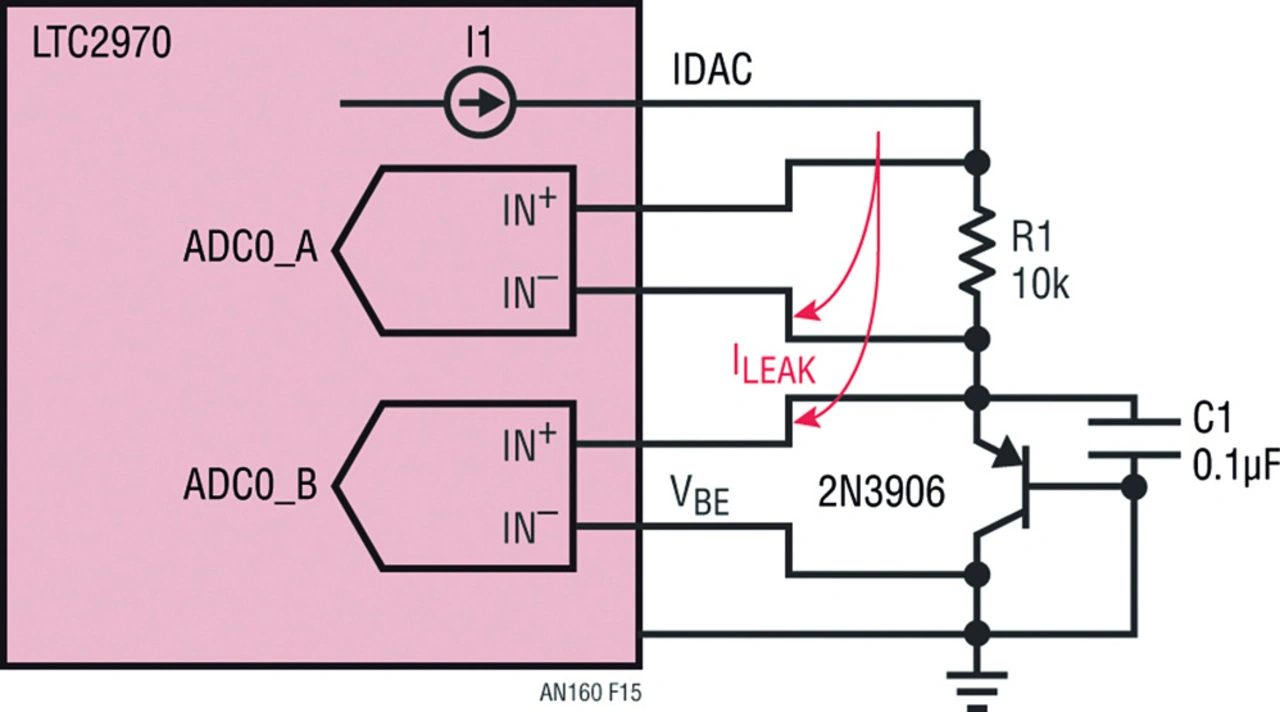
- Eingangsleckströme des A/D-Wandlers
Die Eingangs-Pins des A/D-Wandlers LTC2970 haben keine unendlich hohe Impedanz, sondern lecken etwas. Somit fließt Strom im Messwiderstand, nicht aber durch den Bipolartransistor (Bild 13). Dieser Messstrom beeinträchtigt primär das Verhältnis der Ströme, nicht jedoch die gemessene UBE. Die Größenordnung der Leckströme liegt bei unter 0,1 µA. Es sind zwei Wandlerkanäle mit einem Ende des Widerstands verbunden, sodass die Leckströme maximal 0,2 µA ausmachen. Der Fehler im Verhältnis der Ströme beträgt damit nach Gleichung (15) etwa 0,116.
(15)
Der resultierende Temperaturfehler ist –0,85 K. Dem Datenblatt des LTC2970 ist nicht zu entnehmen, dass dieser Fehler mit hohen Temperaturen zunimmt, sodass er zu einem nichtlinearen Temperaturverstärkungsfehler beiträgt.
- Transistoreigenschaften
Der Nichtidealitätsfaktor n ist in einem gegebenen Transistor im Grunde konstant, variiert aber von Transistor zu Transistor. In einer bestimmten Bauteilfamilie (2N3906) sind die Variationen von n zwischen den Bausteinen gering. Zwischen den einzelnen Bauteilfamilien (2N3906 verglichen mit 2N3904) sind die Unterschiede größer. Es ist wichtig, einen akkuraten Wert für n in den Berechnungen und im C-Code zu verwenden. Die Empfindlichkeit auf kleine Fehler im nichtlinearen Faktor des Transistors wird durch folgende Gleichung beschrieben:
(16)
Bei einer Änderung von n um 0,001 verändert sich die Temperatur um –22,8 mK.
- Stromverstärkung β
Die grundlegende Transistorgleichung für all unserer Berechnungen lautet:
(17)
Aber IC ist nicht gleich dem Eingangsstrom IIn. Ein Teil des Eingangsstroms fließt zur Basis des Transistors, der andere durch den Kollektor. Die Summe davon, der Eingangsstrom, ist auch der Emitterstrom.
Man misst den Strom, der in den Bipolartransistor fließt und berechnet das Verhältnis der gemessenen Ströme (das Verhältnis von IE):
Soweit sich β nicht mit dem angelegten Strom ändert, bleibt auch das Verhältnis der Ströme unverändert. Wenn aber βLOW ungleich βHIGH ist, dann verändert sich das Verhältnis und stört die Temperaturmessung. Wenn z. B. βHIGH 44 und βLOW 40 sind, dann ist die berechnete Temperatur um etwa 0,33 K verfälscht. Für größere Werte von β wird der Temperaturfehler kleiner.
Der vollständige Satz an Temperaturungenauigkeiten ist in Tabelle 1 angegeben. Diese gelten speziell für den LTC2970, der mit einem Transistor 2N3906 arbeitet.
- Temperatur fernabfragen (Teil 2)
- Genauigkeit der Schaltung
- Quantisierung und Rauschen
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Energy Harvesting
PMICs unter die Lupe genommen (Teil 2)
Sequencing mit Powermanagement-ICs
Immer schön der Reihe nach
Energy Harvesting
PMICs unter die Lupe genommen (Teil 1)
Herausforderung Zuverlässigkeit
Überwachung von ICs
System zur Backup-Stromversorgung
Allzeit bereit!
Neue Voraussetzung im Power Management
Mehr Effizienz mit Hochspannung
Interview mit Analog-Guru Bob Dobkin
»Wir haben von Digital sehr profitiert«
