Stromversorgung
Vereinfachte Gleichrichterberechnung
Fortsetzung des Artikels von Teil 1
Berechnung am Einweggleichrichter
Der Fall des Einweggleichrichters unterscheidet sich vom Fall des Zweiweggleichrichters dahingehend, dass nur halb so viel Ladung nachgeliefert wird.
Das bedeutet, dass zur Beschreibung der Zusammenhänge beim Einweggleichrichter in Gleichung 7 der Gewichtsfaktor von 4/3 in 2/3 abgeändert werden muss. Für diesen Fall wird aus Gleichung 11:
Mit wachsendem Laststrom IL fällt UL in diesem Fall erheblich schneller ab. Der Maximalstrom der Gleichrichterschaltung ist auf die Hälfte reduziert. In Analogie zum Zweiweggleichrichter kann auch für den Einweggleichrichter eine näherungsweise Approximation durch einen Widerstand RÄQ angegeben werden. Er ist im Vergleich zum Zweiweggleichrichter etwa doppelt so groß:
Auch hier ist die Näherung über weite Bereiche des Laststroms gut nutzbar. Abgesehen von dem schnelleren Spannungsrückgang findet beim Einweggleichrichter eine Gleichstrom-Vormagnetisierung im Kern statt. Das macht eine andere Auslegung des verwendeten Transformators erforderlich.
Verlustleistung aufgrund Gleichrichtung
Am Innenwiderstand RI des Transformators entstehen Verluste. Diese lassen sich aus Gleichung 6 ableiten. Das Quadrat des Momentanwertes des Stromes multipliziert mit RI stellt den Momentanwert der Verlustleistung dar. Analog zu Gleichung 7 kann der zugehörige Mittelwert berechnet werden:
Setzt man in Gleichung 15 die Ausgangsspannung UL gleich Null, so resultiert ein Wert von:
Bei einer idealen Sinusfunktion müsste der Ausdruck
betragen. Die Abweichung von 2,5 % kommt durch die Parabelapproximation zustande. Dies zeigt zugleich die hohe Güte des verwendeten Modells; gemäß Voraussetzung ist es nur bis UL/U0 = 1/√2 definiert (siehe auch Gleichung 2), liefert aber auch für den Wert UL/U0 = 0 sinnvolle Ergebnisse.
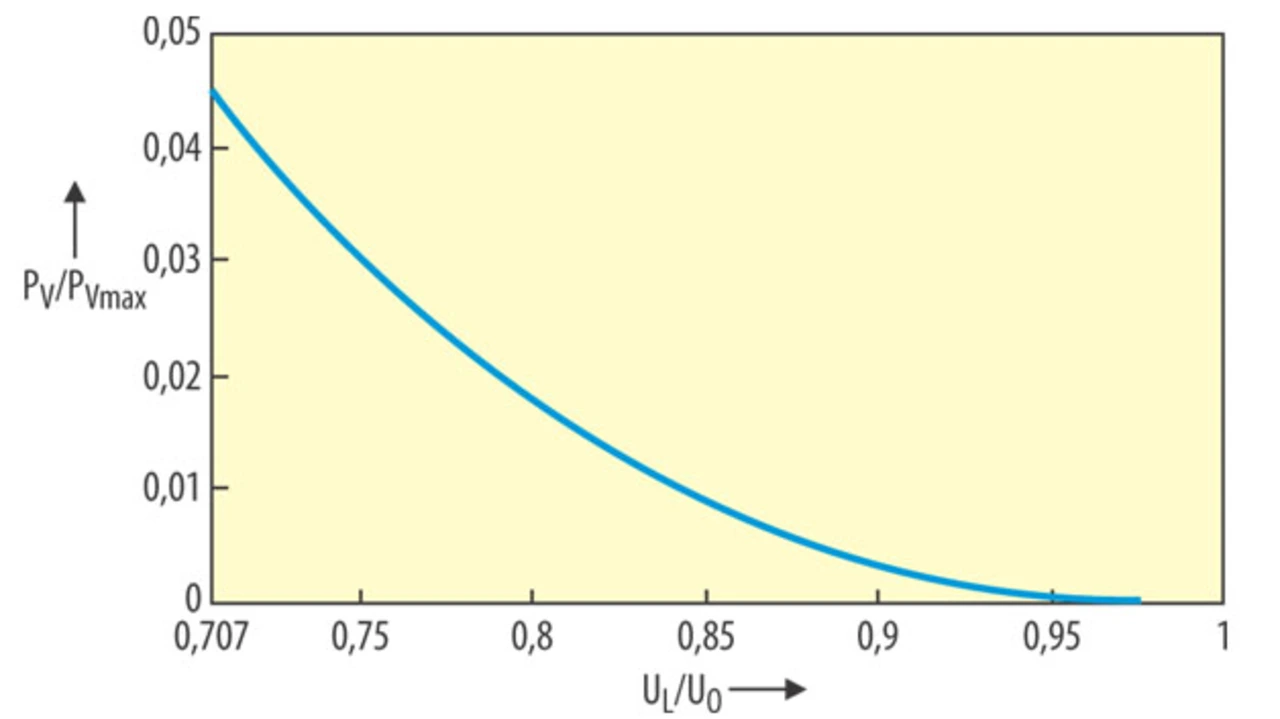
Die normierte Verlustleistung in Abhängigkeit von der Ausgangsspannung ist in Bild 5 dargestellt. Als Normierungsleistung wird PVmax = U02/2RI verwendet. Dabei handelt es sich um die Kurzschlussverlustleistung im Transformator.
Die vergleichsweise kleinen Zahlenwerte an der Leistungsachse in Bild 5 dürfen nicht darüber hinwegtäuschen, dass der Innenwiderstand des Transformators (normalerweise Spannungsquelle) für gewöhnlich klein im Vergleich zur Last gewählt wird. Der Absolutwert der Verlustleistung kann im Vergleich zu der in die Last abgegebenen Nutzleistung ganz erheblich sein, da PVmax große Werte annimmt.
- Vereinfachte Gleichrichterberechnung
- Berechnung am Einweggleichrichter
- Diskussion der Ergebnisse




