Methoden zur Computersimulation von Lithium-Ionen-Akkus
Die virtuelle Batterie
Fortsetzung des Artikels von Teil 1
Batteriesimulationen mit BEST
In der Abteilung „Strömungs- und Materialsimulation“ am Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM werden physikbasierte Kontinuumsmodelle und passende numerische Verfahren zu deren Lösung entwickelt. Hierbei ist die Software BEST, kurz für: Battery and Electrochemistry Simulation Tool, entstanden, die sowohl ein mikroskopisches als auch ein Newman-artiges Zellmodell für Lithium-Ionen-Batterien dreidimensional umsetzt [4].
Das Mikromodell [5] beschreibt den Transport von Ionen und Ladungen durch die zeitliche und räumliche Entwicklung einer Lithium-Konzentration c und eines elektrischen Potenzials Φ, die in jedem Punkt des Simulationsvolumens definiert sind. Aus diesen primären Größen lassen sich andere interessante Größen wie das Zellpotenzial, die interne Stromverteilung oder die räumliche Variation der Überpotenziale berechnen.
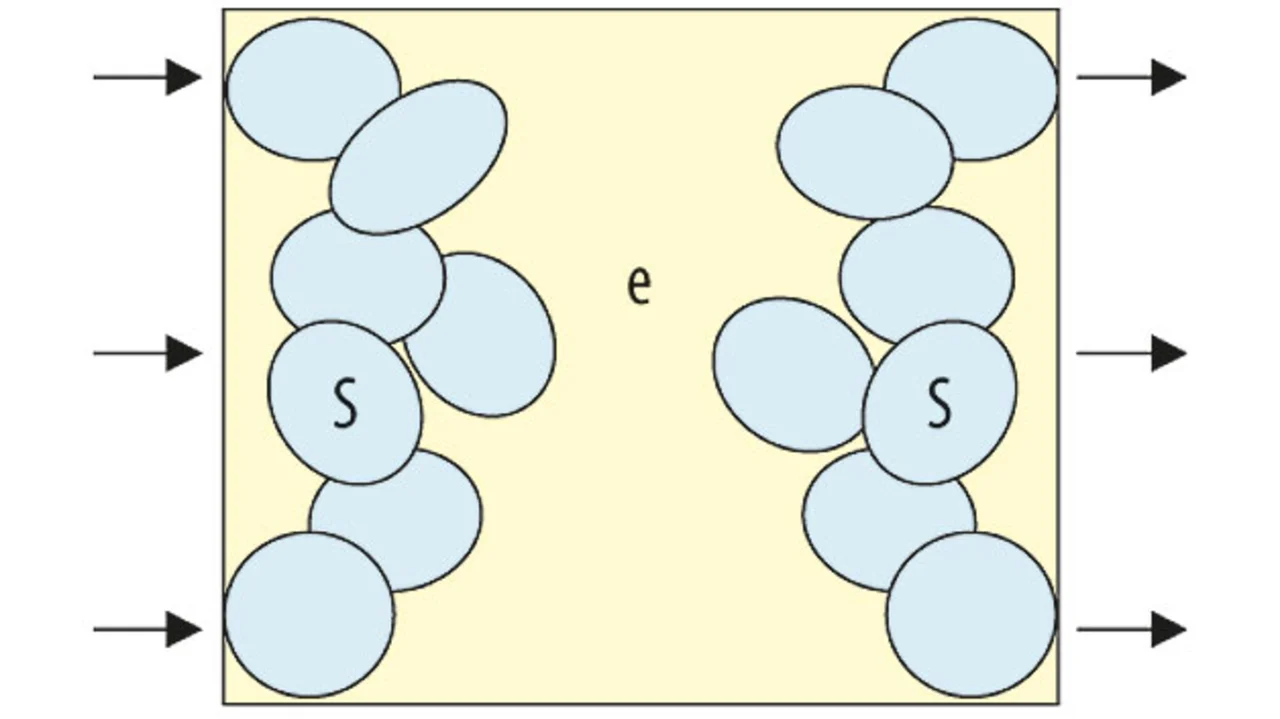
Das Simulationsvolumen selbst ist unterteilt in die Bereiche der positiven und negativen Elektrode sowie den Elektrolyten (Bild 2).
In den beiden Elektroden sind Konzentration und Potenzial unabhängig voneinander: Dort geschieht der Stromtransport über die Elektronen im festen Material (solid, „s“) und wird durch das ohmsche Gesetz beschrieben:
Hierbei ist die lokale Stromdichte, κs die elektrische Leitfähigkeit und Φ das lokale elektrische Potenzial. Die interkalierten Lithium-Ionen gehorchen in vielen Materialien einem Diffusionsgesetz
mit der Diffusionskonstante Ds des Aktivmaterials, dem Ionenfluss und der lokalen Lithium-Ionen-Konzentration c. Es gibt aber auch Aktivmaterialien, die einen Phasenübergang zwischen einer Lithium-reichen und einer Lithium-armen Phase ausbilden. In diesem Fall beschreibt die einfache Diffusion den Ionentransport nicht mehr korrekt und muss z.B. durch kompliziertere Phasenfeldmodelle ersetzt werden. In der Elektrolytregion lassen sich Konzentration und Potenzial nicht mehr getrennt beschreiben, weil es dort ja gerade die positiv geladenen Lithium-Ionen sind, die den Strom transportieren. Der Ladungstransport im Elektrolyten (Subskript „e“) wird hier durch folgende Gleichung bestimmt, die Konzentration und Potenzial koppelt:
wobei t+ die sogenannte Transferzahl, F die Faradaykonstante, R die ideale Gaskonstante und T die absolute Temperatur ist. Entsprechend gibt es eine Gleichung für den Transport der Lithium-Ionen:
Der Stromfluss im Elektrolyten hat also direkten Einfluss sowohl auf die Konzentrations- wie auch die Potenzialgradienten. Wesentlich für das Batterieverhalten sind die (De-) Interkalationsreaktionen an der Grenzfläche zwischen Aktivmaterial und Elektrolyt. An diesen Grenzflächen gehen Lithium-Ionen vom Elektrolyten über in das Aktivmaterial (oder umgekehrt). Mit welcher Rate dies passiert, ist abhängig von der sogenannten Überspannung η, die wiederum von den Konzentrations- und Potenzialverhältnissen auf beiden Seiten der Grenzfläche abhängt:
Aus dieser Formel ergibt sich dann die lokale Stromdichte ise, mit der der Ionenübergang stattfindet:
Eine wichtige Eingangsgröße ist hierbei die individuelle Leerlaufspannung U0 der jeweiligen Elektrode, die vom Ladezustand, also von der Lithium-Ionen-Konzentration der Elektrode, abhängt. Letztlich ist durch die Elektrode mit der höheren Leerlaufspannung die positive und mit der kleineren die negative Elektrode definiert. Die unterschiedliche Leerlaufspannung der beiden Batterieelektroden ist der Grund dafür, dass der Ionentransport von negativer zu positiver Elektrode von selbst stattfindet (Entladen), während für den umgekehrten Prozess (Laden) Energie aufgewendet werden muss.
Anhand der oben aufgeführten Gleichungen wird deutlich, dass zunächst ein gewisser Parametrisierungsaufwand zu leisten ist, bevor das Modell zu konkreten Berechnungen genutzt werden kann. Beispielsweise müssen die Diffusionskonstanten, die Leitfähigkeiten, die Transferzahl oder die Leerlaufpotenziale experimentell oder durch Ab-initio-Methoden ermittelt werden. Des Weiteren ist noch ein Geometriemodell notwendig, innerhalb dessen die Gleichungen gelöst sowie die Randbedingungen, sprich: welcher Strom oder welche Spannung angelegt werden soll, formuliert werden. Für die Lösung der Gleichungen können unterschiedliche numerische Methoden eingesetzt werden. Ziel ist dabei, die partiellen Differenzialgleichungen durch ein geeignetes Diskretisierungsverfahren in ein System algebraischer Gleichungen umzuwandeln. In BEST wird hierzu die sogenannte „Finite-Volumen-Methode“ angewandt, die das Berechungsgebiet in viele kleine quaderförmige Volumina („Voxel“) aufteilt, die jeweils für einen Wert von c und Φ stehen [6].
- Die virtuelle Batterie
- Batteriesimulationen mit BEST
- Lösungen bei den Gleichungssystemen
Das könnte Sie auch interessieren
Akkus
Welche Ladezustands- Bestimmung eignet sich für…
Helmholtz-Zentrum Berlin
Batterie-Elektroden realistisch modellieren
