Sichere Authentifizierung
Produktschutz mit Elliptic Curve Cryptography
Fortsetzung des Artikels von Teil 1
Der mathematische Hintergrund
Die Elliptic-Curve-Kryptografie arbeitet mit Skalaren und Punkten. Während Skalare üblicherweise mit Kleinbuchstaben bezeichnet werden, stellt man Punkte mit Großbuchstaben dar (siehe Tabelle). Für Skalare sind drei Arten numerischer Operationen definiert, nämlich die Addition (+), die Multiplikation (*) und die Inversion (–1). Für Punkte gibt es zwei numerische Operationen: die Addition (+) und die Multiplikation (x). Auch wenn das Symbol ‚+‘ für Skalare und Punkte verwendet wird, folgt die Punktaddition anderen Regeln als die Skalaraddition. Die genannten Operationen sind auf Kurven über Primkörper und auf Kurven über Binärkörper anwendbar. Algebraische Formeln zur Ausführung derartiger Berechnungen finden sich in [3].
Bei den für die ECDSA-Authentifizierung erforderlichen Berechnungen handelt es sich um die Erzeugung eines Schlüsselpaars (privater und öffentlicher Schlüssel), die Berechnung einer Signatur und die Verifikation einer Signatur. Die zugehörigen Gleichungen sind in öffentlich zugänglicher Literatur zu finden [2, 3, 4]. Leider benutzen die verschiedenen Autoren jeweils eigene Konventionen, so dass es schwierig ist, ihren Ausführungen zu folgen. Deshalb sind die Gleichungen hier unter strikter Befolgung der obigen Konventionen noch einmal aufgeführt.
Generierung des Schlüsselpaars
Jobangebote+ passend zum Thema
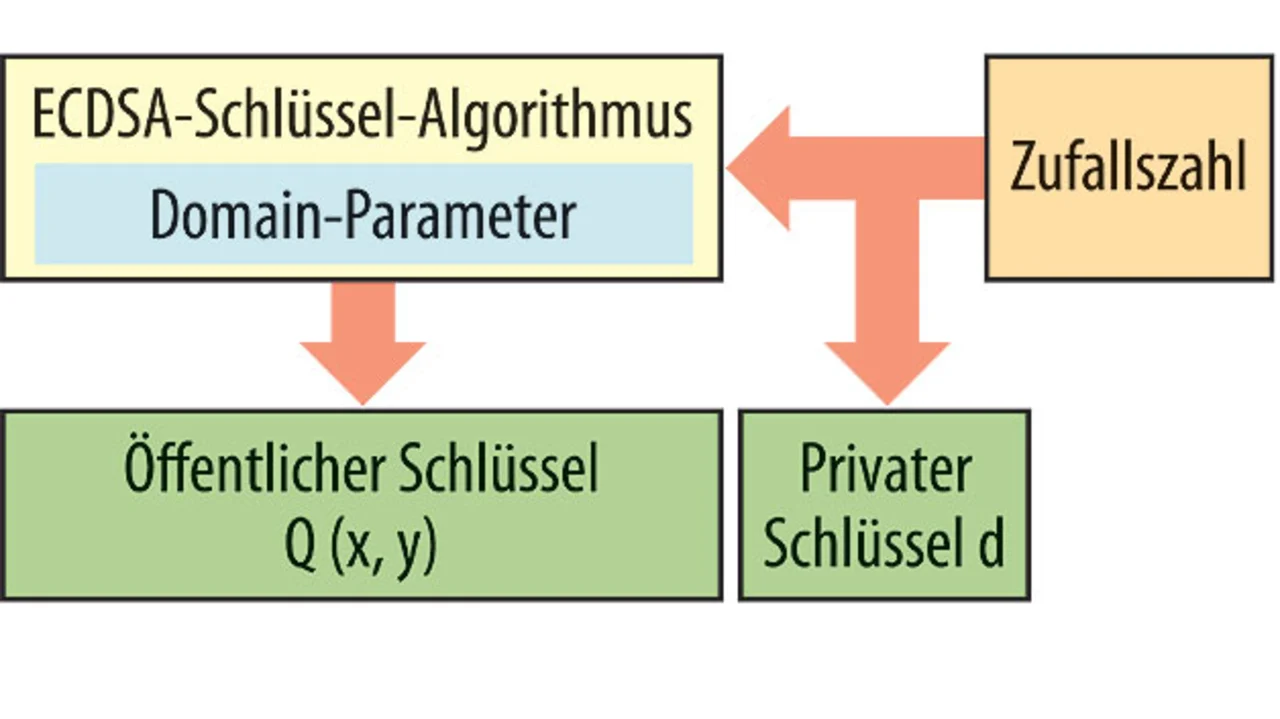
Bevor ein ECDSA Authenticator funktionieren kann, muss er seinen privaten Schlüssel kennen. Der öffentliche Schlüssel wird dagegen aus dem privaten Schlüssel und den Domain-Parametern abgeleitet. Beide Schlüssel müssen im Speicher des Authenticator abgelegt werden, wobei der private Schlüssel – wie der Name schon sagt – für die Außenwelt nicht zugänglich sein darf. Der öffentliche Schlüssel dagegen muss für Lesezugriffe freigegeben sein. Wie die Erzeugung des Schlüsselpaars abläuft, zeigt Bild 2.
Zunächst wird ein Zufallszahlen-Generator gestartet. Dieser gibt einen numerischen Wert aus, der zum privaten Schlüssel d (einem Skalar) wird. Als nächstes wird der öffentliche Schlüssel Q(x,y) mit Gleichung 1 per Punktmultiplikation berechnet:
(1) Q(x, y) = d × G(x, y)
Berechnung der Signatur
Eine digitale Signatur gibt dem Empfänger einer Nachricht die Möglichkeit, deren Authentizität mit Hilfe des öffentlichen Schlüssels des Authenticator zu verifizieren. Hierzu wird aus der Nachricht, deren Länge variieren kann, mit Hilfe eines sicheren Hash-Algorithmus zunächst ein Message Digest h(m) generiert [1].
Ein sicherer Hash-Algorithmus zeichnet sich durch die folgenden besonderen Merkmale aus:
- Er ist irreversibel. Es ist also unmöglich, die ursprüngliche Nachricht rechnerisch aus dem Digest zu rekonstruieren.
- Er ist kollisionsresistent. Es ist praktisch unmöglich, weitere Nachrichten zu finden, die denselben Digest ergeben.
- Starker Lawineneffekt. Jede noch so kleine Änderung an einer Nachricht bewirkt eine wesentliche Veränderung des Digest.
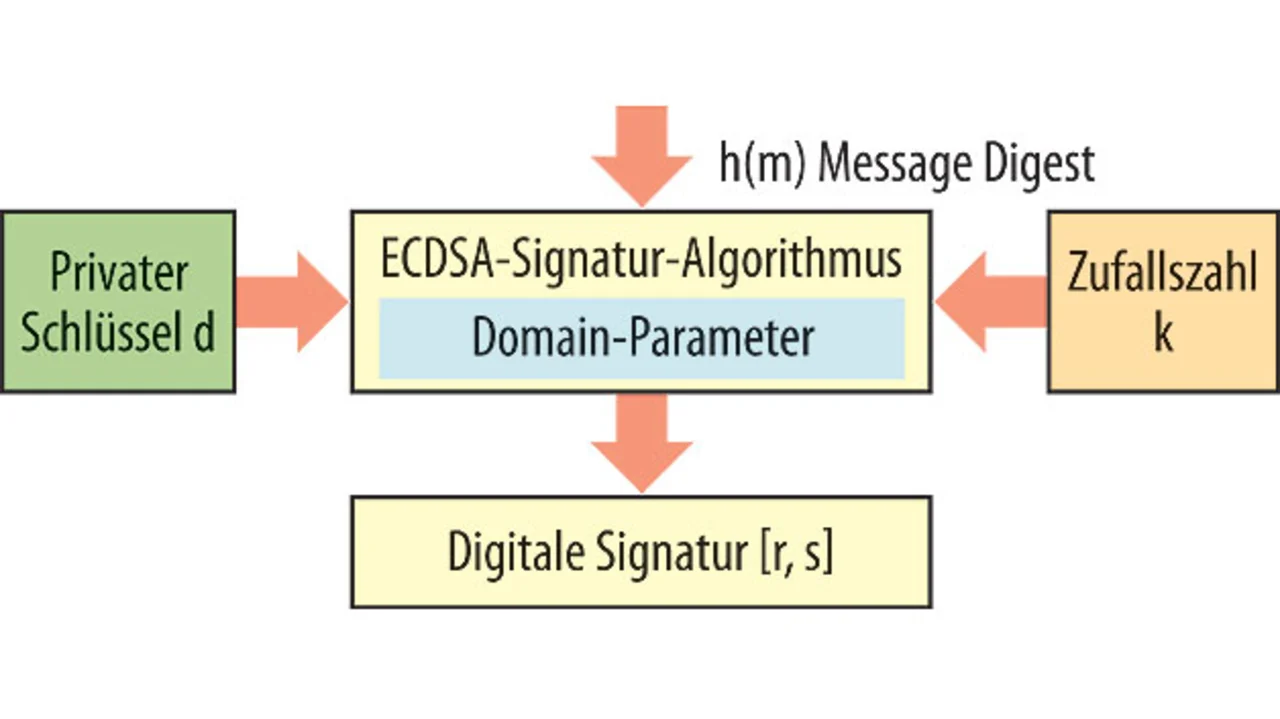
Ist der Digest für die Nachricht berechnet, wird ein Zufallszahlengenerator aktiviert, um einen Wert k für die Elliptic-Curve-Berechnungen zu erzeugen (Bild 3).
Die Signatur besteht aus zwei Ganzzahlen r und s. Gleichung 2 zeigt die Berechnung von r aus der Zufallszahl k und dem Basispunkt G(x,y).
(2) (x1, y1) = k × G(x, y) mod p
r = x1 mod n
Um gültig zu sein, muss r von Null verschieden sein. Tritt der seltene Fall ein, dass r gleich Null ist, muss eine neue Zufallszahl k erzeugt und ein neuer Wert für r berechnet werden.
Nachdem r erfolgreich berechnet wurde, schließt sich die Berechnung von s gemäß Gleichung 3 unter Verwendung von Skalaroperationen an. Als Ausgangswerte dienen der Message Digest h(m), der private Schlüssel d, der zuvor berechnete Wert r und die Zufallszahl k:
(3) s = (k–1 (h(m) + d ∙ r)) mod n
Um gültig zu sein, muss s von Null verschieden sein. Tritt der seltene Fall ein, dass s gleich Null ist, muss eine neue Zufallszahl k erzeugt und ein neuer Wert für r und s berechnet werden.
- Produktschutz mit Elliptic Curve Cryptography
- Der mathematische Hintergrund
- Verifikation der Signatur
- Authentifizierung einer installierten Peripheriekomponente