Sichere Authentifizierung
Produktschutz mit Elliptic Curve Cryptography
Gefälschte Komponenten sind ein Risiko für jeden Gerätehersteller. Eine Möglichkeit, die Produkte zu schützen, stellt die sichere Authentifizierung dar. Die Verwendung eines Authentifizierungssystems basierend auf Elliptic Curve Cryptography ist eine leistungsfähige Lösung hierfür.
Authentifizierungssysteme stützen sich traditionell auf symmetrische Algorithmen wie etwa sichere Hash-Algorithmen. Diese benötigen jedoch geheime Schlüssel [1], deren Management und Schutz sich recht anspruchsvoll gestalten kann. Eine Alternative dazu bietet das ECC-Verfahren (Elliptic Curve Cryptography), bei dem alle beteiligten Geräte über ein Schlüsselpaar bestehend aus einem privaten und einem öffentlichen Schlüssel (Private Key/Public Key) verfügen. Der private Schlüssel wird vom Urheber einer Nachricht zur Erstellung einer Signatur benutzt. Ob die Signatur der Nachricht gültig ist, kann vom Empfänger mit Hilfe des öffentlichen Schlüssels des Absenders verifiziert werden. Sollte die Nachricht auf ihrem Weg zum Empfänger verändert worden sein, fällt die Signaturverifikation negativ aus, da die ursprüngliche Signatur nicht für die modifizierte Nachricht gilt. In dem vom US-amerikanischen National Institute of Standards and Technology (NIST) herausgegebenen Digital Signature Standard (DSS) sind geeignete elliptische Kurven ebenso spezifiziert wie die Berechnung der Schlüsselpaare und digitale Signaturen [2]. Der vorliegende Artikel behandelt das Konzept des Elliptic Curve Digital Signature Algorithm (ECDSA) und schildert, wie sich diese Methode in der Praxis einsetzen lässt.
Elliptische Kurven
Viele Entwickler werden den Begriff ‚elliptisch“ mit den Kegelschnitten aus der längst vergangenen Schulzeit in Verbindung bringen. Eine Ellipse ist ein Sonderfall der allgemeinen Gleichung zweiten Grades der Form ax² + bxy + cy² + dx + ey + f = 0. Je nach den Werten der Parameter a bis f kann es sich bei dem resultierenden Graphen auch um einen Kreis, eine Hyperbel oder eine Parabel handeln. Die ECC-Technik nutzt jedoch Gleichungen dritten Grades.
Jobangebote+ passend zum Thema
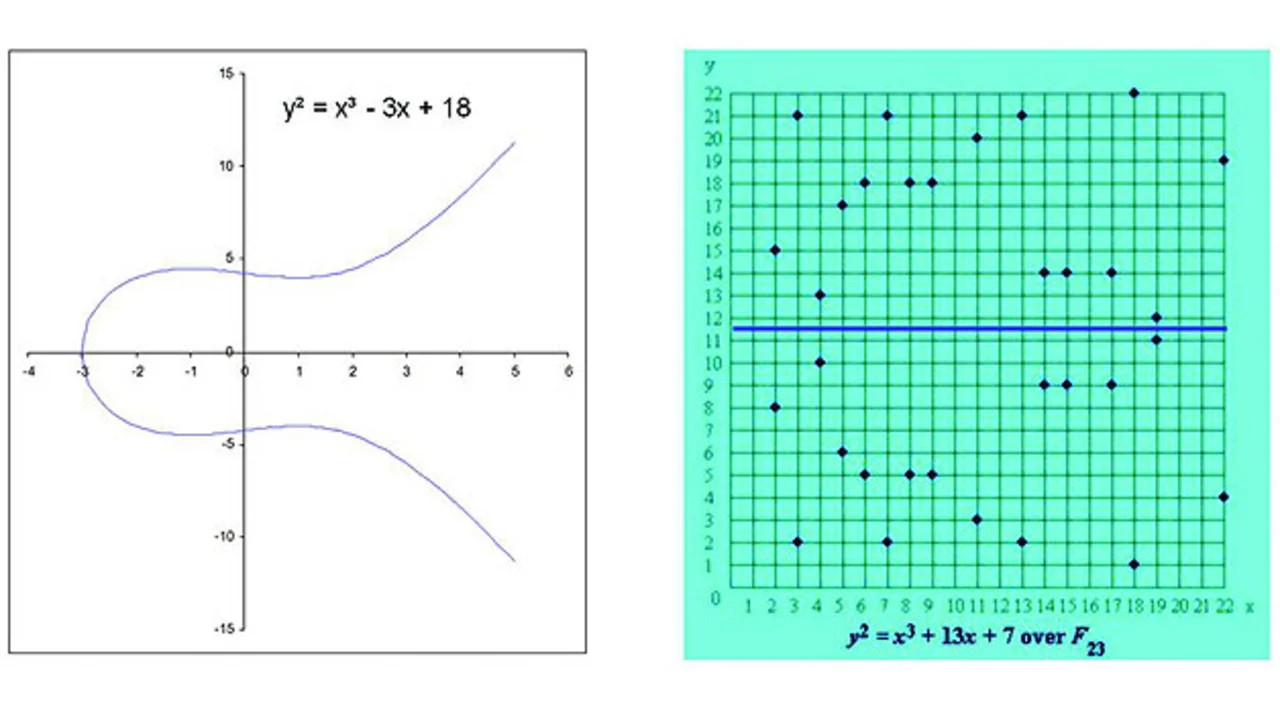
Der DSS definiert zwei Arten elliptischer Kurven für den Einsatz mit dem ECC-Verfahren. Die Koeffizienten von pseudozufälligen Kurven werden aus dem Resultat einer auf einem Startwert beruhenden kryptografischen Hash-Funktion generiert. Bei den „speziellen“ Kurven werden die Koeffizienten und der zugrundeliegende Körper so gewählt, dass die Effizienz der Elliptic-Curve-Operationen optimiert wird. Pseudozufällige Kurven können über Primkörper GF(p) und Binärkörper GF(2m) definiert werden.
Ein Primkörper ist ein Körper GF(p), bei dem die Zahl der Elemente (p) eine Primzahl ist. Die Elemente dieses Körpers sind die ganzen Zahlen modulo p. Die Körperarithmetik wird mit der Arithmetik der ganzen Zahlen modulo p implementiert. Die anwendbare elliptische Kurve hat die Form y² = x³ +ax + b. Bild 1 zeigt ein Beispiel einer elliptischen Kurve im reellen Bereich und über einen Primkörper modulo 23. Ein gemeinsames Merkmal ist die vertikale Symmetrie.
Ein Binärkörper ist der Körper GF(2m), der für einen Wert m (die Ordnung des Körpers) 2m Elemente enthält. Die Elemente eines solchen Körpers sind die Bit Strings der Länge m. Die Körperarithmetik ist in Form von Operationen mit den Bits implementiert. Die passende elliptische Kurve hat die Form y² + xy = x³ + ax² + b.
Grundsätzlich wird diese Gleichung von praktisch unendlich vielen möglichen Kurven erfüllt. Für das ECC-Verfahren ist jedoch nur eine geringe Anzahl von Kurven relevant, die in der FIPS-Publikation 186 als „NIST Recommended Elliptic Curves“ aufgelistet sind (FIPS = Federal Information Processing Standard). Jede Kurve wird mit ihrem Namen und einer Domain-Parameter-Menge definiert. Letztere besteht aus dem Primmodulus p, der Primordnung n, den Koeffizienten a und b sowie den x- und y-Koordinaten des Basispunkts G(x, y) auf der Kurve. Die Tabelle gibt exemplarisch die Domain-Parameter der Kurve P-192 wieder, bei der es sich um eine pseudozufällige Kurve über einen Primkörper handelt. Weitere Beispiele finden sich in [2]. Der numerische Teil des Kurvennamens gibt die Länge des privaten Schlüssels in bit an. Der Umfang des öffentlichen Schlüssels und der digitalen Signatur entspricht der doppelten Länge des privaten Schlüssels.
| Parameter | Notation | Wert |
|---|---|---|
| Primmodulus p | Dezimal | 6277101735386680763835789423207666416083908700390324961279 |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFFFF FFFFFFFF | |
| Primordnung n | Dezimal | 6277101735386680763835789423176059013767194773182842284081 |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF 99DEF836 146BC9B1 B4D22831 | |
| Koeffizient a | Dezimal | –3 (identisch mit p – 3) |
| Hex | FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFFFF FFFFFFFC | |
| Koeffizient b | Hex | 64210519 E59C80E7 0FA7E9AB 72243049 FEB8DEEC C146B9B1 |
| x-Koordinate des Basispunkts G(x,y) | Hex | 188DA80E B03090F6 7CBF20EB 43A18800 F4FF0AFD 82FF1012 |
| y-Koordinate des Basispunkts G(x,y) | Hex | 07192B95 FFC8DA78 631011ED 6B24CDD5 73F977A1 1E794811 |
Domainparameter der Kurve P-192
- Produktschutz mit Elliptic Curve Cryptography
- Der mathematische Hintergrund
- Verifikation der Signatur
- Authentifizierung einer installierten Peripheriekomponente