Code-Optimierung
Implementierung eines schnellen FIR-Filters mit dem Atom-Prozessor
Fortsetzung des Artikels von Teil 1
10 240 statt 70 480 Taktzyklen
Bei der Analyse des Codestücks unter Berücksichtigung der Architektureigenschaften der Atom-CPU (ggf. unter Zuhilfenahme des Vtune Performance Analyzers) lassen sich verschiedene Leistungsbremsen identifizieren. Als erstes wäre da die Latenzzeit der Multiplikationsanweisung: Zwar kann in jedem zweiten Prozessortakt eine SIMD-Multiplikation ausgeführt werden (Durchsatz), aber es dauert fünf Takte, bis das Ergebnis vorliegt und von anderen Instruktionen weiterverarbeitet werden kann (Latenz). Falls das Multiplikationsergebnis, wie hier, früher verwendet wird, so fügt die CPU Wartezyklen ein (In Order Execution, im Gegensatz zu den großen Brüdern Core 2 oder Core-i7, die in solchen Fällen die Reihenfolge der Befehle zur Laufzeit geeignet umstellen: Out of Order Execution). Des Weiteren liegt der Satz von acht Eingangswerten der inneren Schleife im Allgemeinen nicht auf einer 16-byte-Grenze im Arbeitsspeicher (Unaligned Load). Alignment ist schwer erfüllbar, da in der äußeren Schleife der Vektor- Zeiger immer um einen Wert (zwei Bytes) weiterrückt. Deswegen wird der spezielle Ladebefehl movups verwendet, der kein Alignment erfordert, aber mehrere extra CPU-Zyklen zur Ausführung braucht. Ein weiteres Problem sind skalare Code-Abschnitte. Die Nutzlast der äußeren Schleife, d.h. das Aufsummieren der Akkumulatoren, Skalieren auf 16 bit und Abspeichern des Ergebnis-Samples, geschieht zwar mittels SIMD-Befehlen, aber im Wesentlichen auf skalaren Daten ohne Ausnutzung der SIMDFähigkeiten der Intel-Architektur. Der in der inneren Schleife erzielte hohe Datendurchsatz wird dadurch relativiert. Ebenfalls bremsend wirken horizontale Rechen-Operationen. Das „horizontale“ Aufsummieren der vier 32-bit-Akkumulatoren mittels der Anweisung phaddd in der äußeren Schleife ist zwar eine sehr bequeme, aber eine relativ „teure“ Anweisung, die mehrere CPU-Zyklen in Anspruch nimmt.
Vermeiden der Latenzzeit von Multiplikationen
Schlüssel für eine leistungssteigernde Umformung des Filter-Codes ist die Technik des „Loop Unrolling“: Die innere Schleife (die bei Filterlänge 63 achtmal ausgeführt wird) wird vollständig, d.h. achtmal entrollt. Bei jeder Instanz wird ein anderes 128-bit-Arbeitsregister verwendet, d.h. xmm2 statt xmm1, dann xmm3 usw. Damit verschwindet nicht nur der (geringe) Overhead der inneren Schleife. Die so entstehende Befehlsfolge kann nun auch leicht so umgeordnet werden, dass zwischen einer Multiplikation und Aufsummierung des Ergebnisses genügend andere Instruktionen liegen, so dass unnötige Wartezeit vermieden wird. Listing 3 zeigt die vollständig ausgerollte innere Schleife des Filter- Codes, wobei die einzelnen Instanzen verschieden eingerückt sind, um die Herleitung aus dem Code von Listing 2 zu verdeutlichen. Man erkennt deutlich, wie die Ergebnisse der pmaddwd- Instruktionen erst fünf (oder mehr) Befehle später weiterverwendet werden, um Wartezyklen zu vermeiden. Die Ausführungszeit für das Filtern eines Datensatzes von 640 Werten sinkt damit erheblich und beträgt in dieser Version ca. 45 000 Taktzyklen.
Jobangebote+ passend zum Thema

Unaligned Load
Man sieht, dass der Zeiger [esi], über den die Eingangswerte des Filters eingelesen werden (immer 128 bit, das heißt 8 Werte auf einmal), mit jedem Durchlauf der äußeren Schleife um 2 byte (16 bit) weitergezählt wird. Wenn die 640 Eingangswerte auf einer 16-byte-Grenze im Adressraum liegen, ist also im ersten Durchlauf 16-byte- Alignment gegeben; im zweiten sind alle Zugriffe um 2 byte versetzt usw., bis im 9. Durchlauf wieder der günstige Fall des 16-byte-Alignments vorliegt. Sieben von acht Fällen sind somit nicht 16-byte-aligned. Um dem abzuhelfen, ist es zunächst notwendig, auch die äußere Schleife achtfach zu entrollen. In der ersten der acht nun entstandenen Instanzen sind nun sicher alle adeoperationen 16- byte-aligned. Für die zweite Instanz hilft folgender Trick: Statt von [esi+2] wird erneut von [esi] gelesen. Man erhält also nur sieben brauchbare Werte. Diese werden nun per pmaddwd mit einer Kopie der Filterkoeffizienten verknüpft, in der alle Koeffizienten ebenfalls um 2 byte verschoben sind (Bild 2).
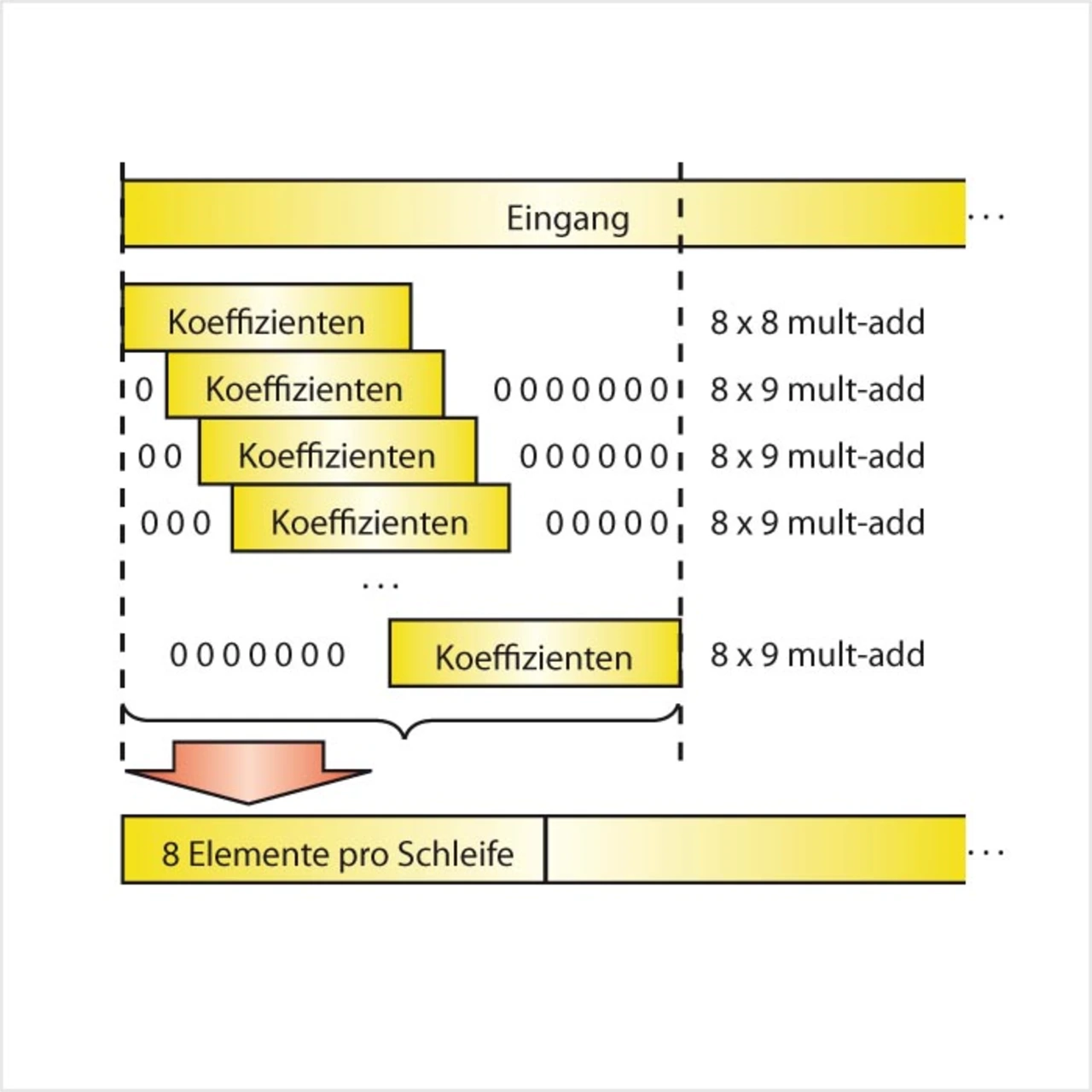
Damit erhält man in den vier Akkumulatoren die korrekten ersten Teilsummen für die zweite Filterantwort. Um zu verhindern, dass der unbrauchbare Wert x0 das Ergebnis beeinflusst, wird in der Kopie der Filterkoeffizien Filterkoeffizienten an dieser Stelle Null eingefügt (Padding). Nach dem selben Schema verfährt man für die restlichen 57 Filterkoeffizienten, die im zweiten Schleifendurchgang benötigt werden, wobei der letzte 64. Filterkoeffizient wiederum mit Null aufgefüllt werden muss, um das Ergebnis nicht zu verfälschen. In der dritten Instanz werden wieder Eingangswerte ab [esi] gelesen und mit einer weiteren Kopie der Filterkoeffizienten verknüpft, in der alle Werte um 4 byte verschoben sind. Das Ganze wiederholt sich dann entsprechend. Insgesamt sind neben dem Original sieben je um 2 byte verschobene Kopien der Filterkoeffizienten notwendig, die aber einmal angelegt werden und deshalb kaum Rechenzeit beanspruchen (Bild 3). Durch das Padding werden die Kopien der Filterkoeffizienten von 64 auf 71 Einträge ausgeweitet, was auch einen etwas erhöhten Rechenaufwand bedeutet (knappe 11 %). Andererseits sind durch diesen Trick nun alle Speicherzugriffe 16-byte-aligned und es kann der schnellere Ladebefehl movaps verwendet werden. In der Summe sinkt die Ausführungszeit trotz des Zusatzaufwandes dramatisch auf ca. 17 000 Taktzyklen.
Ersetzen von skalaren Code-Abschnitten durch SIMD-Code
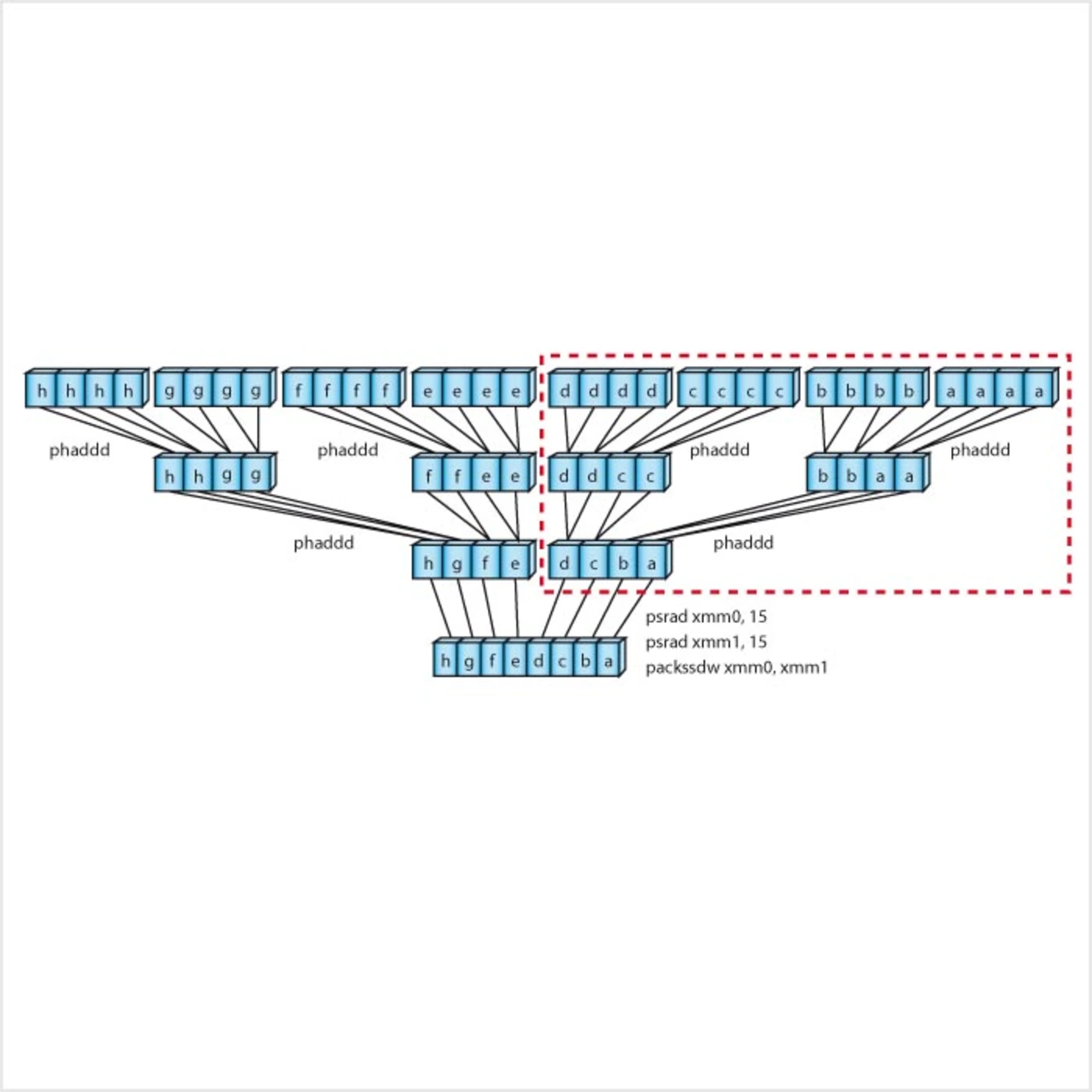
Mit dem achtfachen Ausrollen der äußeren Schleife ist auch die Lösung des oben aufgeführten Problems „skalarer Code“ näher gekommen. Nachdem nun pro Schleifendurchlauf acht Mal vier Teilakkumulatoren aufsummiert werden, lassen sich die Schritte „Aufsummieren und Skalieren der Teilergebnisse“ mit SIMD-Anweisungen erledigen, wie in Bild 4 illustriert ist. Um 8x4 32-bit-Werte in acht 16-bit-Werte zu komprimieren, werden benötigt: sechs horizontal adds, zwei 128-bit-shifts, ein 128-bit-pack (statt ursprünglich 16 horizontal adds, acht 128-bit-shifts, acht 128-bit-pack). Für die genaue Funktionalität der verwendeten Befehle sei auf [1] verwiesen. Der so modifizierte Code läuft nun in 15 300 CPU-Zyklen ab.
- Implementierung eines schnellen FIR-Filters mit dem Atom-Prozessor
- 10 240 statt 70 480 Taktzyklen
- Vermeiden horizontaler Rechenoperationen