Startseite > Power > Energiespeicher > Voltage-Mode-Regler

Regelungstechnik – Teil 5 von 6

Voltage-Mode-Regler

25. November 2019, 15:34 Uhr | Von Dr. Ali Shirsavar, Dr. Michael Hallworth und Florian Hämmerle

Im fünften Teil der Artikelserie soll der erste Regler so ausgelegt werden, dass der Eintaktflusswandler stabilisiert wird.

Mit den ersten vier Teilen der Artikelserie hat Omicron Lab das Basiswissen für die Auslegung von Netzteil-Reglern geschaffen. Als Nächstes soll nun der erste Regler so ausgelegt werden, dass ein Eintaktflusswandler stabilisert wird.

▶ Diesen Artikel anhören

Die verschiedenen Netzteil-Regler wurden in den vorangegangenen Beiträgenim Detail erläutert. Mit dem Wissensstand der bisherigen Artikel, ist es nun möglich, den ersten Regler auszulegen, um einen Eintaktflusswandler per Voltage-Mode-Regler zu stabilisieren. Das in diesem Teil vorgestellte Auslegungsverfahren kann auf alle hart schaltenden, nicht isolierten Eintaktflusswandler mit oder ohne Transformator angewendet werden: zum Beispiel Abwärts, Eintaktfluss, Gegentaktfluss, Halbbrücke und Vollbrücke. Im finalen Beitrag wird dann die Current-Mode-Regelung im Detail erklärt.

Aber zuerst ein paar Worte zur Voltage-Mode-Regelung: Die Voltage-Mode-Regelung ist eine der ersten Formen der Schaltnetzteil-Regelung. Ihre Funktionsweise ist sehr einfach, da lediglich die Ausgangsspannung betrachtet wird. Bei einem Spannungsanstieg wird der PWM-Tastgrad reduziert und bei fallender Ausgangsspannung wird er erhöht. Somit reguliert man nur die Ausgangsspannung in Bezug zur Soll- beziehungsweise Referenzspannung. Das dynamische Verhalten der Änderung des Tastgrads wird vom entworfenen Regler beziehungsweise von der Position seiner Pol- und Nullstellen bestimmt. Der Regler sollte eine schnelle Sprungantwort liefern und gleichzeitig gewährleisten, dass die Stabilitätskriterien eingehalten werden.

Auslegung eines Voltage-Mode-Reglers

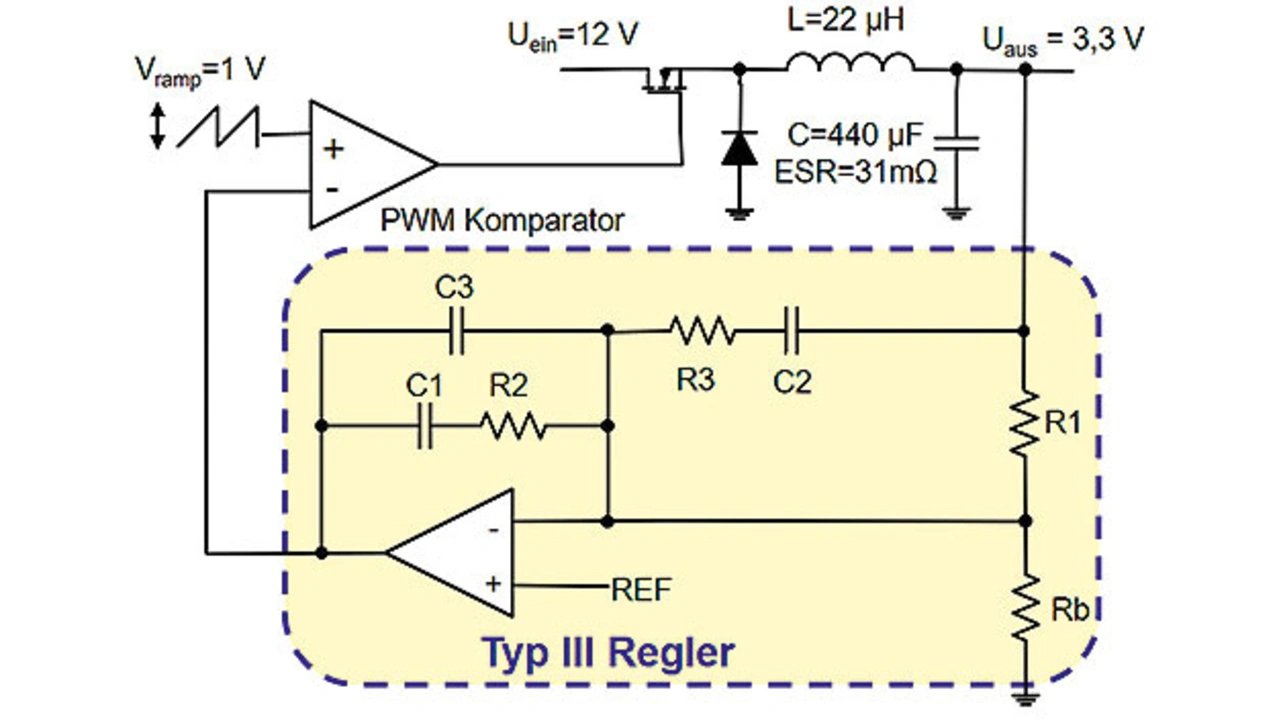
Für eine Voltage-Mode-Regelung ist fast immer ein Typ-III-Regler (Bild 1) nötig. Aus den vorangegangenen Beiträgen sind die Übertragungsfunktion H(s) und die Gleichungen bekannt, welche die Pol- und Nullstellen mit den Komponentenwerten in Beziehung setzen:

(1) $H subscript left parenthesis straight s right parenthesis space end subscript equals space left parenthesis straight omega subscript straight p 0 end subscript over s right parenthesis space cross times space fraction numerator left parenthesis s over straight omega subscript straight z 1 end subscript plus 1 right parenthesis left parenthesis s over straight omega subscript straight z 2 end subscript plus 1 right parenthesis over denominator left parenthesis s over straight omega subscript straight p 2 end subscript plus 1 right parenthesis left parenthesis s over straight omega subscript straight p 3 end subscript plus 1 right parenthesis end fraction$

Wichtig ist, dass diese Gleichungen in rad/s angegeben sind, obwohl gewöhnlich mit Hz gearbeitet wird. Darum müssen die Ergebnisse mit dem Faktor 2π umgerechnet werden.

(2) $straight omega subscript straight p 0 end subscript space equals fraction numerator 1 over denominator straight R subscript 1 left parenthesis straight C subscript 1 space plus space straight C subscript 3 right parenthesis end fraction straight omega subscript straight p 2 end subscript space equals space fraction numerator straight C subscript 1 space plus space straight C subscript 3 over denominator straight R subscript 2 straight C subscript 1 straight C subscript 3 end fraction straight omega subscript straight p 3 space end subscript equals space fraction numerator 1 over denominator straight R subscript 3 straight C subscript 2 end fraction straight omega subscript straight z 1 space end subscript equals fraction numerator 1 over denominator straight R subscript 2 straight C subscript 1 end fraction straight omega subscript straight z 2 end subscript equals space fraction numerator 1 over denominator straight C subscript 2 left parenthesis straight R subscript 1 space plus straight R subscript 3 right parenthesis end fraction$

Hierbei sind ω_p0, ω_p2 und ω_p3 die Polstellen und ω_z1 und ω_z2 die Nullstellen des Reglers. Die WDS-Software zur automatischen Netzteilauslegung von Biricha entwirft automatisch hochgradig optimierte Regler, wie in den vorangegangenen Beiträgen beschrieben. Sind die Anforderungen an das Einschwingverhalten jedoch nicht sehr hoch, kann für die meisten Abwärtswandler und nicht isolierte Eintaktfluss-Topologien problemlos ein stabiler Regler von Hand ausgelegt werden. Aus dem Schaltbild des Abwärtswandlers in Bild 1 lassen sich alle notwendigen Werte ablesen.

Bode-Diagramm der Regelstrecke ermitteln

Das Bode-Diagramm der Regelstrecke sieht für alle im Voltage-Mode geregelten Eintaktflusswandler einfach aus. Zum Beispiel kann ein Abwärtswandler auch als Eintaktflusswandler mit einem Transformator-Windungsverhältnis von 1:1 dargestellt werden. Wird der PWM-Übertragungsblock vorerst ignoriert, erhält man typischerweise einen Resonanzbuckel bei 1 / (2π√LC) und eine ESR-Nullstelle bei 1 / (2π x ESR x C). Mit den in Bild 1 dargestellten Werten für L, C und ESR können die Positionen des Resonanzbuckels und der ESR-Nullstelle im Bode-Diagramm der Regelstrecke leicht berechnet werden (Bild 2). In Bild 2 ist ersichtlich, dass die Niederfrequenz-Verstärkung im Gegensatz zu einem standardmäßigen LC-Filter nicht 0 dB beträgt, da der PWM-Generator die sogenannte »PWM-Verstärkung« verursacht.

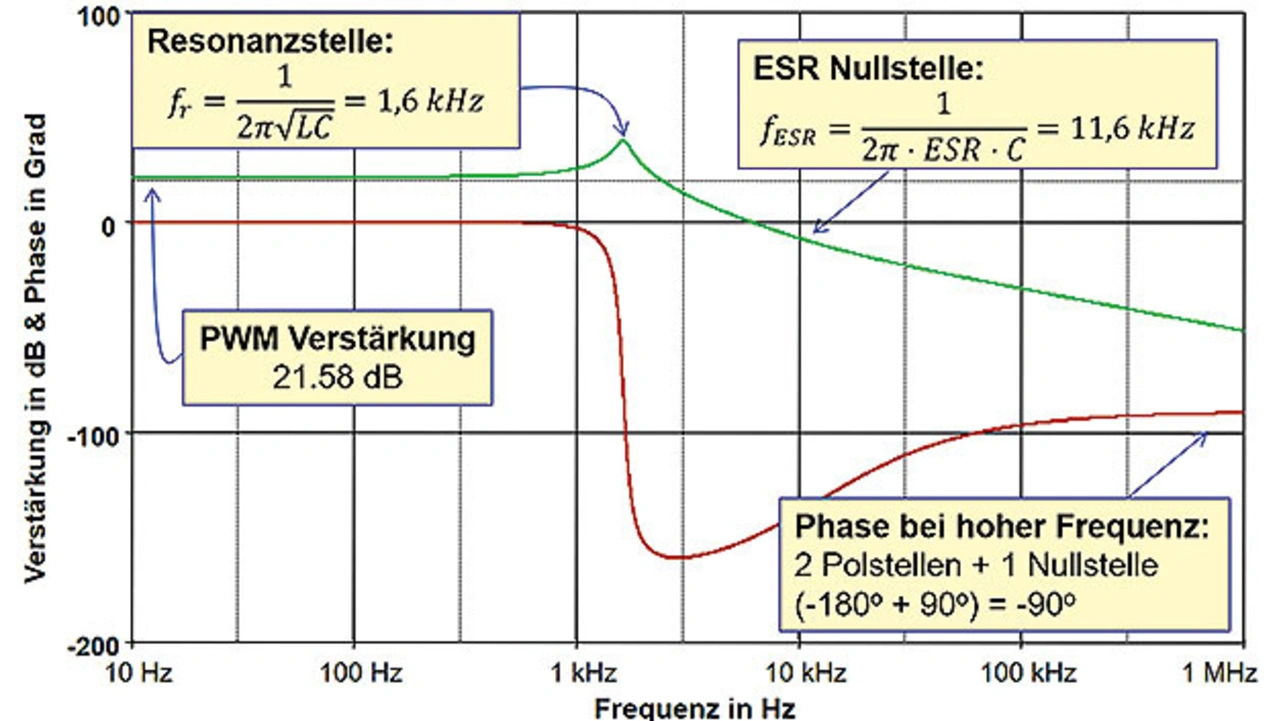
Für Voltage-Mode-Abwärtswandler ist diese Verstärkung einfach zu berechnen. Sie entspricht der Eingangsspannung dividiert durch die Sägezahnamplitude des PWM-Generators (V_ramp in Bild 1). Die Eingangsspannung – hier 12 V – ist bekannt und die Sägezahnamplitude ist stets im Datenblatt des integrierten Schaltkreises (IC) angegeben. In diesem Fall beträgt die Niederfrequenz-Verstärkung somit 20 x log(12 V / 1 V) = 21,58 dB.

Wenn ein Transformator in der Schaltung verbaut ist, muss nur noch der Amplitudengang um das Transformator-Windungsverhältnis skaliert werden. Dadurch ist das Bode-Diagramm der Regelstrecke vollständig und es kann mit der Regler-Auslegung begonnen werden.

Position der Pol-/Nullstellen des Reglers

Die vorgestellte Methode stellt eine einfache Annäherung dar, um die Werte für einen leistungsfähigen Regler samt angemessener Durchtrittsfrequenz zu berechnen. Es gibt allerdings präzisere Methoden und einige Bücher, die detailliertere Analysen auflisten [1][2][3]. Auch die WDS-Software setzt auf präzise Gleichungen, damit der Benutzer die genaue Phasenreserve und Durchtrittsfrequenz ermitteln kann. Für das hier verwendete Beispiel genügt im Moment jedoch ein Taschenrechner und ein Blatt Papier.

Aus der Übertragungsfunktion des Reglers ist ersichtlich, dass es nur zwei Polstellen, zwei Nullstellen und einen Integrator gibt. Folgende Anleitung bringt ausreichend gute Eigenschaften und Stabilität:

Zwei Nullstellen des Reglers werden an der Resonanzstelle platziert – zum Beispiel bei 1,6 kHz
Eine Polstelle des Reglers wird verwendet um die ESR-Nullstelle zu kompensieren – zum Beispiel bei 11,6 kHz
Die zweite Polstelle des Reglers wird bei der halben Schaltfrequenz positioniert – zum Beispiel bei 100 kHz wenn die Schaltfrequenz 200 kHz be- trägt–, um hochfrequentes Rauschen zu unterdrücken

Zuletzt wird die Position des Integrators nach der folgenden Gleichung berechnet wobei an Stelle von fx der Wert der gewünschten Durchtrittsfrequenz eingesetzt wird:

$f subscript p 0 end subscript equals fraction numerator V subscript r a m p end subscript cross times f subscript x over denominator U subscript e i n end subscript end fraction space space space left parenthesis 3 right parenthesis$

In dem hier dargestellten Beispiel ist eine Durchtrittsfrequenz von f_x = 10 kHz gewünscht. Nach Gleichung 3 muss der Integrator bei f_p0= 1 V .10 kHz⁄12 V = 833 Hz platziert werden.