Voltage-Mode-Regler

Komponentenwerte des Reglers berechnen

Da nun die Positionen der Pol- und Nullstellen des Reglers bekannt sind, können mit Gleichung 2 die Komponentenwerte Schritt für Schritt berechnet werden:
In der Regel wird mit der Berechnung von R₁ und R_b begonnen, basierend auf der Stromstärke, die durch beide fließen soll, und der für den integrierten Schaltkreis (IC) des Reglers benötigten Referenzspannung. Als Nächstes muss gewährleistet werden, dass die Verlustleistung pro Widerstand 60 mW nicht überschreitet, damit kein Hitzestau auf der Leiterplatte riskiert wird. Außerdem sollte die Stromstärke aus Gründen der Robustheit während des Störfestigkeitstests in der EMV-Prüfkammer nicht unter 100 µA fallen.

• R₁ und R_b bilden einen Spannungsteiler, woraus sich die erforderliche Referenzspannung ergibt – beim aktuellen Beispiel wird davon ausgegangen, dass sie 2,55 V beträgt. Die Eingangsspannung des Spannungsteilers – Uaus = 3,3 V – und die dem IC zugeführte Ausgangsspannung des Spannungsteilers (2,55 V) ist also bekannt. Angefangen bei einer Stromstärke von 1 mA, die durch den Spannungsteiler fließen soll und mit Hilfe der üblichen Spannungsteiler-Regel ergibt sich: R₁ = 750 Ω, R_b = 2,55 kΩ sowie eine Verlustleistung pro Widerstand < 60 mW.
• Da R₁ mittlerweile bekannt ist, kann die Gleichung für ωp0 verwendet werden, um C₁ zu berechnen. Zur Erinnerung: Die Gleichungen sind alle in rad/s angegeben, weshalb eine Umrechnung mit dem Faktor 2π nötig ist. Außerdem ist C₁ in der Regel viel größer als C₃ und daher vereinfacht sich die Gleichung für ωp0 zu ωp0 = 1 ⁄ (R1 C1). R₁ und ω_p0 sind bekannt. Somit kann C₁ berechnet werden. Dabei ist C₁ = 1 ⁄ (2π x 833 Hz x 750 Ω) = 250 nF.
• Die Gleichung für ωz1 ist abhängig von C₁ und R₂. Da ω_z1 und C₁ bekannt sind, ergibt sich für R₂ = 390 Ω.
• Da C₁ >> C₃ gilt, vereinfacht sich die Gleichung für ω_p2 zu ω_p2= 1 ⁄ (R2 x C₃). Die Polstelle wird an der ESR-Nullstelle platziert – bei 11,6kHz. Alle Terme mit Ausnahme von C₃ sind bekannt, womit C₃ berechnet werden kann: C₃ = 34 nF.
• Schließlich bleiben noch die Gleichungen für ω_p3 und ω_z2. Beide hängen voneinander ab, aber mit zwei Gleichungen und zwei Unbekannten lässt sich dieses Problem mathematisch lösen. Wird die Gleichung für ω_p3 durch die Gleichung für ω_z2 geteilt, kürzen sich sowohl die Terme für C₂ als auch 2π heraus und übrig bleiben ausschließlich bekannte Variablen. Somit kann nach R₃ aufgelöst werden:

Nach Berechnung von R₃ (R3 = 12 Ω) wird der Wert in die Gleichung für ω_p3 eingesetzt. Nun kann der letzte Komponentenwert berechnet werden: C₂ = 130 nF.

Überprüfung der Berechnung mit Hilfe von WDS

In der WDS-Designsoftware von Biricha können im Modus „manual pole/zero placement“ die Berechnungen einfach überprüft werden. WDS liefert alle wichtigen Stabilitätsparameter sowie das Bode-Diagramm. Das aus dem WDS stammende Bode-Diagramm und die Informationen zur Stabilität des Systems sind in Bild 3 dargestellt.

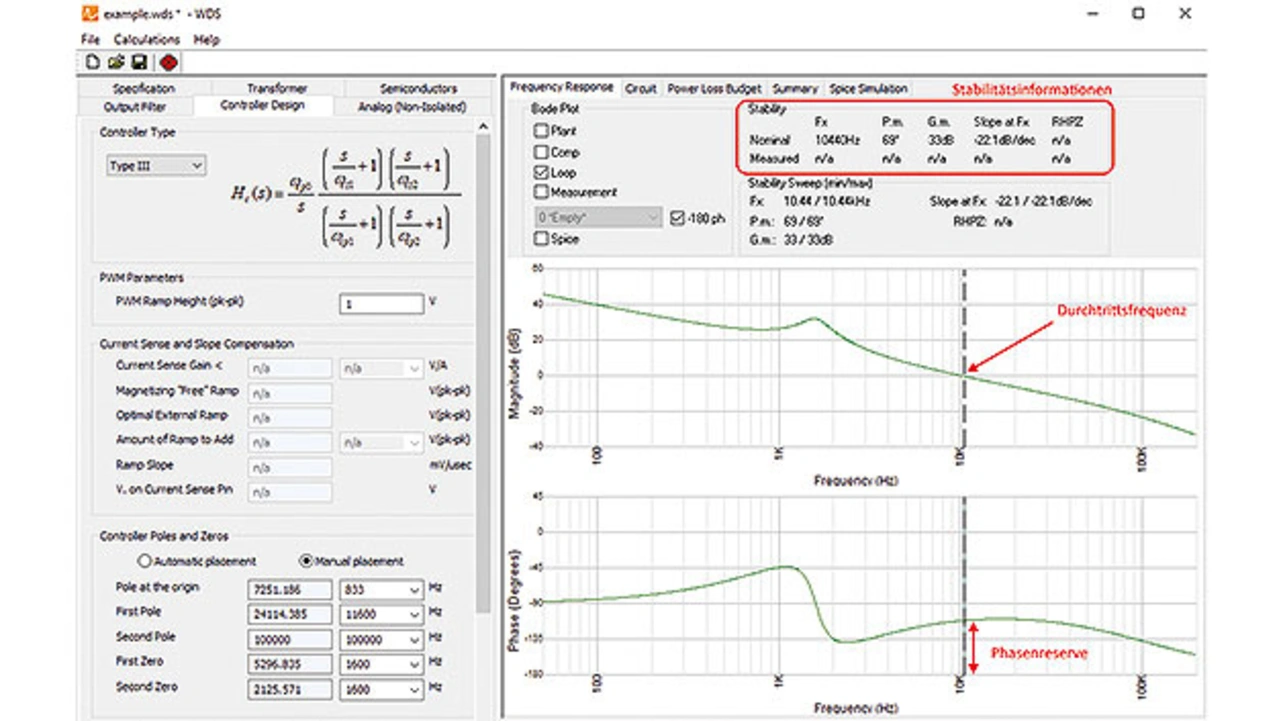
In der Grafik ist ersichtlich, dass die angestrebte Durchtrittsfrequenz von 10 kHz und eine Phasenreserve von 69 Grad erreicht wurde. Der Anstieg bei Durchtritt beträgt etwa -20 dB pro Dekade und die Amplitudenreserve ist größer als 30 dB. Auf diese Weise wurde ein äußerst stabiles Netzteil mit einer respektablen Durchtrittsfrequenz entworfen und obwohl die Phase nicht dezidiert betrachtet wurde, ist die Phasenreserve mit 69 Grad mehr als ausreichend.

Auslegung eines Voltage-Mode-Reglers mit Transformator

Wenn ein Eintaktflusswandler einen Transformator aber keine Isolierung aufweist – zum Beispiel keinen Optokoppler –, dann erfolgt die Auslegung genauso, wie oben beschrieben, mit einer kleinen Ausnahme. Lediglich die Polstelle im Ursprung muss mit dem Transformator-Windungsverhältnis multipliziert werden. Steht beispielsweise ein Eintaktflusswandler mit den exakt gleichen Spezifikationen wie der in diesem Beitrag behandelte Abwärtswandler zur Verfügung, jedoch mit einem Transformator-Wicklungsverhältnis von 10:1, dann müsste lediglich die Polstelle im Ursprung mit dem Faktor 10 multipliziert werden (833 Hz . 10 = 8,33 kHz). Die restlichen Berechnungen und Vorgehensweisen sind dieselben.

So geht es weiter

Im finalen Beitrag wird noch die Current-Mode-Regelung erläutert. Außerdem wird näher ausgeführt, warum es im Allgemeinen nicht sin-nvoll ist, einen PID-Regler zur Stabilisierung eines Voltage-Mode-Netzteils zu verwenden.

Literatur

[1] Biricha Digital’s Analog Power Supply Design Workshop Manual.
[2] Sanjay Maniktala, Switching Power Supplies A-Z.
[3] Christophe Basso, Switch-Mode Power Supplies, Second Edition: SPICE Simulations and Practical Designs.

1. Voltage-Mode-Regler
2. Komponentenwerte des Reglers berechnen
3. Die Autoren

Lesen Sie mehr zum Thema

Das könnte Sie auch interessieren

Regelungstechnik – Teil 6 von 6

Peak-Current-Mode-Regler

Regelungstechnik – Teil 3 von 6

Übertragungsfunktionen verstehen

Regelungstechnik – Teil 4 von 6

Regler für Netzteile

Messen des Regelkreisverhaltens

Stabilität von Schaltnetzteilen

Regelungstechnik – Teil 2 von 6

Messung des Frequenzgangs

Regelungstechnik – Teil 1 von 6

Stabilität von Netzteilen