Implementierung eines Sobel-Filters in C und Assembler
Kamerabasierte Verkehrszeichen-Erkennung
Fortsetzung des Artikels von Teil 2
Kamerabasierte Verkehrszeichen-Erkennung
Der Compiler hat diesmal zwei Hardware-Schleifen erstellt: Es wird dabei nicht von der Möglichkeit Gebrauch gemacht, zwei arithmetische Operationen in einer Anweisungszeile auszuführen. Stattdessen wird immer nur ein Datum parallel zu einer arithmetischen Anweisung geladen. All dies kommt aus der Unsicherheit, die Daten könnten in Abhängigkeit stehen. So multiplizieren sich die zusätzlichen Anweisungen in der inneren Schleife und die Anweisungen zwischen der inneren und äußeren Schleife zu einer großen Zahl an Prozessorzyklen. Daher werden für die Ausführung einer Faltung über diesen Bereich mindestens 18 958 Zyklen benötigt.
Mit Hilfe von zwei Compiler-Pragmas wird dem Compiler mitgeteilt, dass keine Datenabhängigkeit besteht (#pragma no_alias) und dass alle Rechenoperationen parallelisiert werden können (#pragma vector_for). Zusätzlich werden die Matrizen verschachtelt angeordnet (SobelMatXY[]). Es existiert nur noch eine Tabelle mit Werten, die abwechselnd zur Matrix x und Matrix y gehören. Mit einem Zugriff können nun beide Werte aus dem Speicher geholt werden (Listing 3).
Der Compiler kann alle Operationen maximal parallelisieren. Es bleiben noch die Anweisungen für die Vorund Nachbereitung der Operationen übrig. Für die Ausführung werden 7438 Zyklen benötigt. Trotz einer Verbesserung um Faktor 2,5 zeigte Standard-Sobel in C die besseren Ergebnisse. Dies liegt am Entfernen von redundanten Operationen und Nutzen von Synergieeffekten von Gx und Gy, was bei der Standard-Faltung nicht berücksichtigt werden kann. Hinzu kommt, dass zwei Schleifen mit geringer Durchlaufzahl verwendet wurden.
Sobel-Filter im Assembler-Code
Jetzt wird gezeigt, wie die Faltung zweier Matrizen für das Sobel-Filter im Assembler-Code erstellt werden kann. Für die korrekte Funktionsweise müssen, wie bei Standard-Sobel in C, drei Zeilen im internen Speicher zur Verfügung stehen. Für die Vergleichbarkeit wurde eine Zeilenlänge von 256 Bildpunkten verwendet. Der Zugriff auf Bilddaten und Matrixwerte findet über die Adresszeiger des DAG (Data Address Generator) statt. Für die Faltungen müssen jeweils vier Adresszeiger initialisiert werden. Der erste zeigt auf die Filtermatrix selbst (i0). Die folgenden drei Adresszeiger verweisen auf die jeweiligen Zeilen der Bilddaten (i1, i2, i3).
Im Folgenden werden nun immer zwei Faltungen pro Anweisung ausgeführt, eine für Gx und eine für Gy. Die wichtigste Aufgabe ist es hier, die einzelnen Adresszeiger so zu behandeln, dass nach einem Schleifendurchlauf bereits gültige Adressen für den nächsten Durchlauf zur Verfügung stehen. Dies müsste sonst durch zusätzliche Anweisungen realisiert werden. Nach der Faltung ist für nachfolgende Verarbeitungsschritte meist die geometrische Addition erforderlich. Hierfür müssen die Ergebnisse Gx und Gy quadriert und dann miteinander addiert werden (Gxy 2 = Gx 2 + Gy 2). Listing 4 zeigt, wie mit Hilfe von zwei verschachtelten Matrizen (ConvMat-XY[]), Gx und Gy in einer Schleife berechnet werden können. Wie beim optimierten Sobel-Filter wird pro Anweisungszeile ein Bildpunkt mit jeweils einem Matrixpunkt der Matrix x und einem Matrixpunkt der Matrix y berechnet. Nach jeder 3×3-Faltung können nun Gx und Gy quadriert und sofort addiert werden. In der Zeile mit dem Label „lEnd:“ wird quadriert, und in der mittleren Zeile werden die quadrierten Werte addiert. Diese Umsetzung bedarf bei einer Zeilenlänge von 256 Bildpunkten 2560 Zyklen für die Faltung inklusive geometrischer Addition.
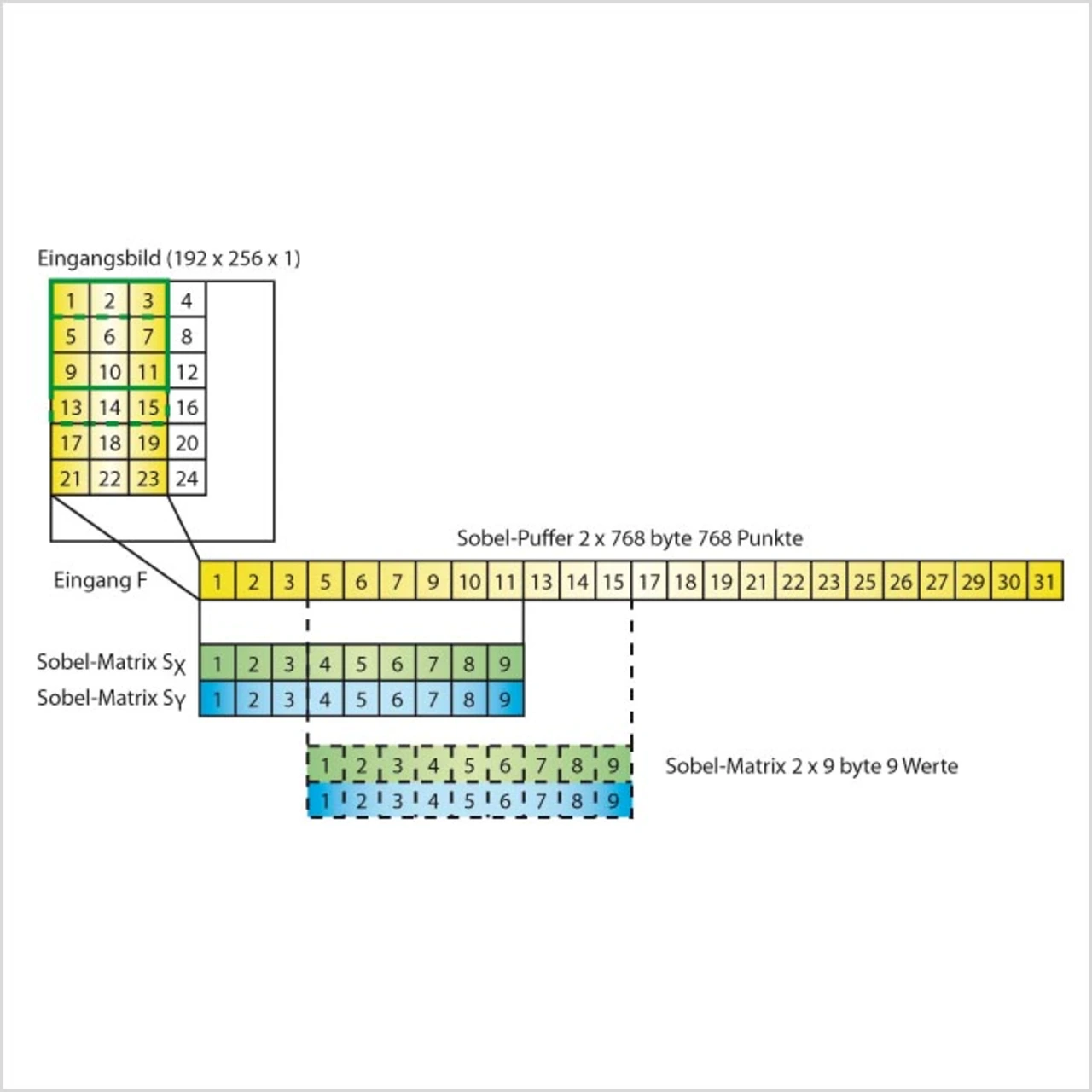
Eine zweidimensionale Faltung besteht somit aus der Summe von neun Multiplikationen. Für das Sobel-Filter müssen zwei Faltungen pro Bildpunkt ausgeführt werden, eine für Kanten in horizontaler Richtung Gx und eine für Kanten in vertikaler Richtung Gy. Aus den Ergebnissen können anschließend die tatsächliche Kantenstärke Gxy und der tatsächliche Winkel Theta ermittelt werden. In Gleichung (2) sind die Sobel-Operatoren gezeigt. Die Gleichungen (3) und (4) zeigen die Berechnungen, die durch Einsetzen der Matrixwerte entstehen.
Da die Sobel-Operatoren mehrere Nullen in der Matrix aufweisen, kann die Anzahl der Multiplikationen reduziert werden. Wie man sieht, werden nur noch sechs Akkumulationen benötigt. Da die Matrizen der Sobel-Operatoren einige Positionen mit 1 belegen, muss dort keine Multiplikation stattfinden. Nur die Positionen mit dem Wert 2 müssen genauer betrachtet werden. Alternativ kann dies aber auch durch Schieben um 1 nach links realisiert werden. Dies macht die Berechnung per Sobel so effizient. Die Intensität jeder Kante wird durch die geometrische Addition der Werte Gx und Gy berechnet. Der Ergebnisvektor zeigt dies durch seine Länge an, wie in den Gleichungen (5) und (6) dargestellt.

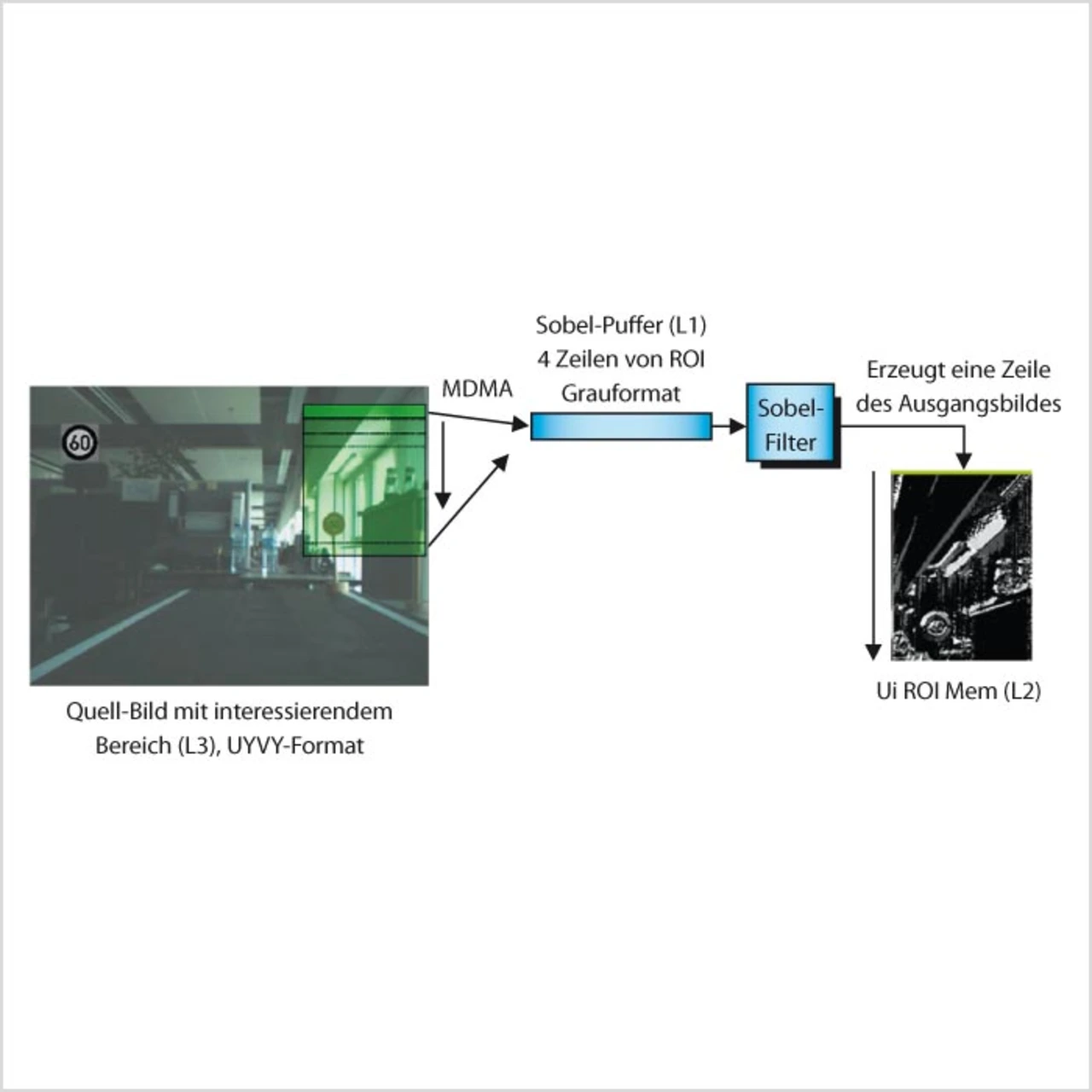
Zunächst wird Gleichung (5) und Gleichung (3) direkt eingesetzt. Eine Region (192 × 256 × 8 bit) des im externen Speicher liegenden Bildes wird zeilenweise ausgelesen und in den internen Speicher transferiert. Es liegen nun drei Zeilen der gewünschten Region in 16 bit Breite im Speicher (3 × 192 × 16 bit) und die Berechnung kann beginnen. Zeitgleich wird die vierte Zeile in den internen Speicher übertragen; sie wird für die Berechnung der zweiten Zeile benötigt. Auf Grund dieser Vorgehensweise werden nach und nach alle Zeilen übertragen und berechnet, während die jeweils alte Zeile verworfen wird. Bild 2 zeigt die Vorgehensweise schematisch. Da die Zeilen im internen Speicher nicht mehrfach umkopiert werden sollen, werden die Zeiger immer wieder neu berechnet. Bild 3 zeigt die Speicheraufteilung und den Lauf der Zeiger a, b und c. Der Programmcode in Listing 1 zeigt, wie die Faltung implementiert wurde. Die Variablen a, b und c zeigen auf die jeweils aktuellen Zeilen. Die Ergebnisse Gx und Gy werden verschachtelt in einer Tabelle abgelegt. Speicherzugriffe sind nur noch für Bilddaten nötig, da die Koeffizienten direkt in die Gleichung codiert wurden. So konkurrieren die Zugriffe für Bilddaten nicht mit Zugriffen auf Koeffizienten-Matrizen. Hinzu kommt, dass manche Operationen im ersten Abschnitt deckungsgleich mit einigen im zweiten Abschnitt sind. Der Compiler erkennt diese Wiederholungen und reduziert die Anzahl der Operationen. Die FOR-Schleife wird durch eine Hardware-Schleife ersetzt. Für pipeline-basierte Prozessoren hat dies einen großen Vorteil: Die Anweisungen innerhalb der Schleife werden pro Iteration automatisch wieder in die Pipeline geschoben, ohne dass Strafzyklen vergeben werden.
- Kamerabasierte Verkehrszeichen-Erkennung
- Die Ermittlung des Winkels
- Kamerabasierte Verkehrszeichen-Erkennung
- Kamerabasierte Verkehrszeichen-Erkennung