Implementierung eines Sobel-Filters in C und Assembler
Kamerabasierte Verkehrszeichen-Erkennung
Fortsetzung des Artikels von Teil 1
Die Ermittlung des Winkels
Nachdem die Faltung an Hand verschiedener Versionen diskutiert wurde, wird nun der Winkel Theta des Vektors berechnet. Für die Winkelberechnung ist es nicht nötig, drei Zeilen zur Verfügung zu stellen. Wie zu sehen war, wurden die Ergebniswerte Gx und Gy bereits verschachtelt gespeichert. In dieser Form können sie nun an die erste Version der Winkelberechnung übergeben werden. Der Zeiger „pInputXY[]“ beginnt mit dem ersten Wert der Zeile Gx, gefolgt von dem ersten Wert der Zeile Gy. Die berechneten Winkelwerte werden mit Hilfe des Zeigers „pOutputPhaseXY[]“ zurückgeschrieben. Auch hier soll die Zeilenlänge 256 Bildpunkte betragen (nCount = 256). Wie zu sehen ist, wird der Winkel mit Hilfe der Arkus-Tangens-Funktion aus der Standardbibliothek berechnet (). Dennoch gehört sie zu den optimierten Versionen, denn sie ist in Assembler codiert und berücksichtigt das Fractional-Format des Prozessors. So kommen keine Gleitkomma-Berechnungen zum Einsatz, die dieser Festkomma-Prozessor per Software emulieren müsste.
Die Anzahl der benötigten Zyklen kann bei dieser Version variieren. Abhängig vom Datenwert werden mehr oder weniger Berechnungen stattfinden müssen, um einen möglichst genauen Winkel zu approximieren. Da für alle Versionen das gleiche Testbild genutzt wurde, können die Ergebnisse untereinander verglichen werden. Für die Berechnung von 256 Bildpunkten wurden 24 000 Zyklen benötigt.
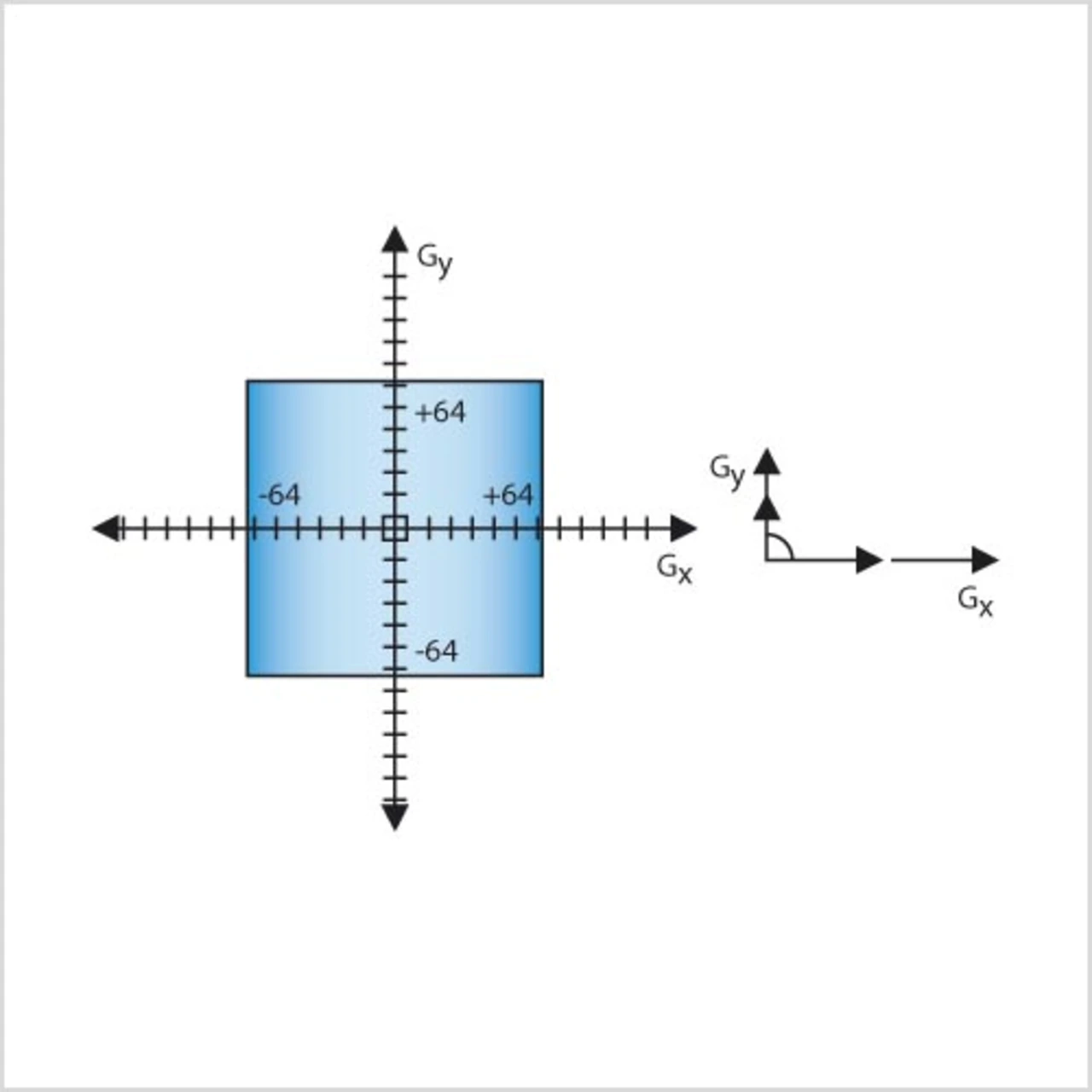
Die Berechnung der Winkel kann auch mittels Arkus-Tagens-Tabelle durchgeführt werden. Die Werte Gx und Gy einer zugehörigen Bildkante identifizieren eine Position in der Arkus-Tangens-Tabelle. In dieser Position ist der zugehörige Winkel zu finden. Hierfür ist zuvor eine Tabelle an zulegen, die eine ausreichende Winkelauflösung zur Verfügung stellt. Wie in Bild 5 zu sehen ist, wurde eine Tabelle der Größe 128 × 128 erstellt. Sie ist mittig zentriert und bietet somit die Winkel für Bildkanten im Wertebereich von –64 bis +64. Für alle Kantenstärken, welche diesen Bereich überschreiten, muss eine Normierung stattfinden. Diese wird erreicht, indem man den größten der beiden Werte (Gx, Gy) so oft teilt (Division = Wert nach rechts schieben), bis er kleiner oder gleich 64 wird. Um trotzdem einen korrekten Winkel zu erhalten, muss auch der kleinere der beiden Werte proportional reduziert werden (Listing 6).
Die Anzahl der benötigten Zyklen ist in diesem Verfahren konstant. Es werden 8493 Zyklen für eine Zeile mit 256 Bildpunkten benötigt. Ein Großteil der Zyklen wird benötigt, um die Werte auf Überschreitung des Bereichs zu untersuchen. Diese Untersuchung kann möglicherweise effizienter gelöst werden.
Die integrierte Winkel-Ermittlung im Assembler-Code
In dieser Variante wurde die optimierte Faltung in Assembler-Code verwendet und die Winkel-Ermittlung in dieser integriert. So müssen die benötigten Werte nicht zweimal aus dem Speicher gelesen beziehungsweise zurückgeschrieben werden.
Wie in Listing 7 zu sehen ist, enthält der Prozessor Anweisungen, die es erlauben, effizient die Größe der einzelnen Werte zu ermitteln und auch zu normalisieren. So werden keine bedingten Sprünge benötigt, die zusätzliche Zyklen verursachen (Prozessor-Pipeline-Effekte). Die Anzahl der benötigten Zyklen ist konstant. Es werden 5915 Zyklen für eine Zeile mit 256 Bildpunkten benötigt.
Die Ergebnisse zeigen, dass auch ein C-Compiler unter Berücksichtigung der jeweils verwendeten Prozessor-Architektur gute Ergebnisse erzielen kann. fr
 | Dipl.-Ing. (FH) Thorsten Lorenzen |
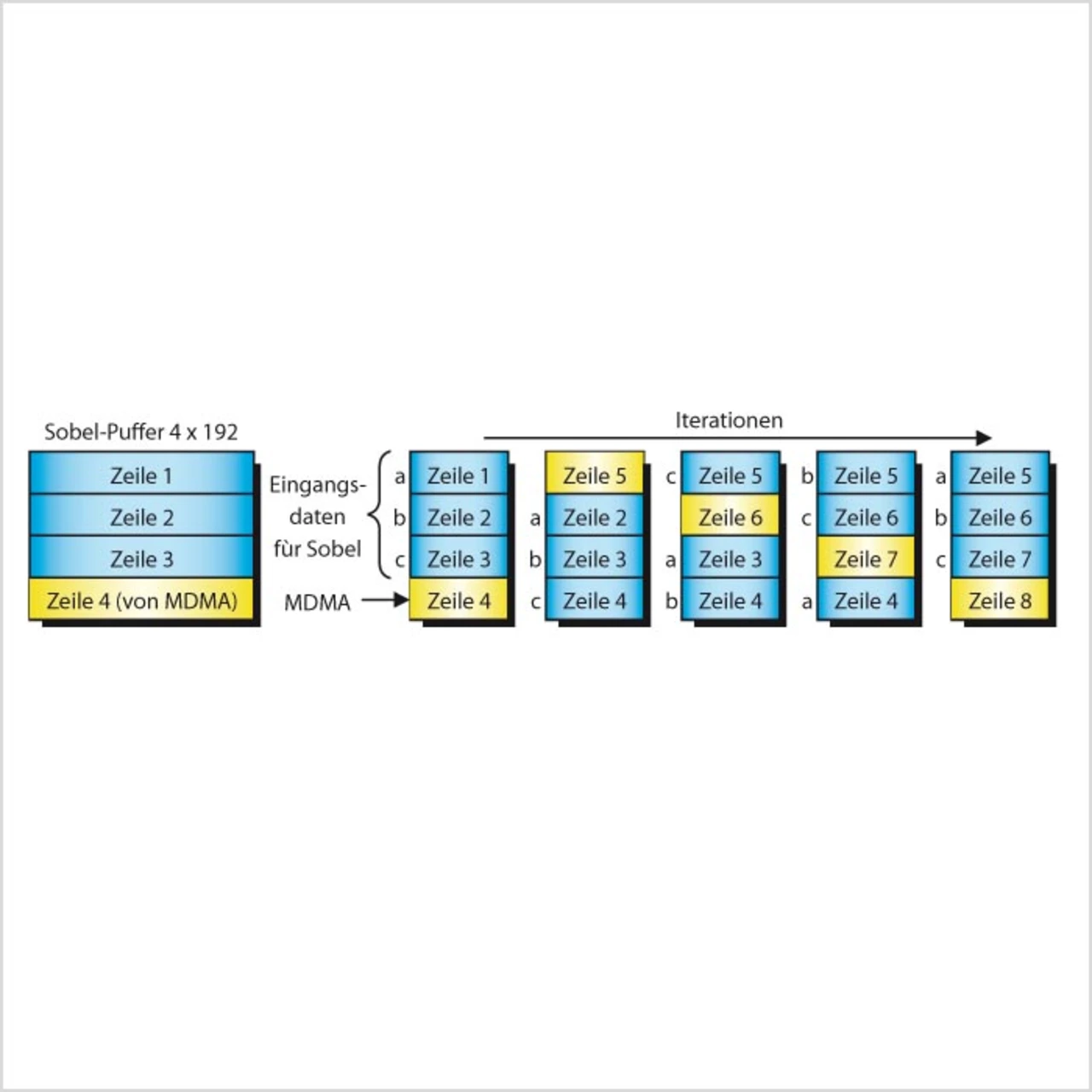
Listing 2 zeigt den eingesetzten C-Code. In der inneren Schleife sind zwei Operationen zu finden. Sie stellen jeweils eine Faltung dar, die aber auf zwei verschiedene Faltungsmatrizen angewendet werden. Durch die lineare Anordnung der Daten per DMA-Kanal kann die Faltung mit einer Adresserhöhung von 1 vollzogen werden. Das passt besser zur Architektur des Blackfin-Prozessors. Nach neun Iterationen der inneren Schleife muss die äußere Schleife eine Adress-Aktualisierung um 3 vornehmen. Damit wird garantiert, dass die Matrizen jeweils eine Zeile nach unten verschoben werden.
- Kamerabasierte Verkehrszeichen-Erkennung
- Die Ermittlung des Winkels
- Kamerabasierte Verkehrszeichen-Erkennung
- Kamerabasierte Verkehrszeichen-Erkennung