Antennenarrays – Teil 2
Strahlungsdiagramme: Gitterkeulen und Beam Squint
Fortsetzung des Artikels von Teil 1
Überlegungen zum Abstand der Antennenelemente
Sollte der Abstand der Antennenelemente also immer kleiner als λ/2 sein? Die Antwort lautet: nicht unbedingt. Vielmehr muss hier beim Entwurf der Antenne eine Abwägung vorgenommen werden. Wird der Abstrahlwinkel komplett auf den Horizont ausgerichtet, so ist θ = ±90 ° und ein Elementabstand von λ/2 ist notwendig, wenn in der sichtbaren Halbkugel keine Gitterkeulen erlaubt sind. In der Praxis aber ist der maximal erreichbare Ablenkwinkel stets kleiner als 90 °, was sich aus dem Elementfaktor und weiteren, bei großen Ablenkwinkeln auftretenden Beeinträchtigungen begründet.
Aus dem Arkussinus-Diagramm in Bild 17 lässt sich entnehmen, dass bei einer Begrenzung der y-Achse (θ) die Gitterkeulen nur bei Scan-Winkeln entstehen, die ohnehin nicht genutzt werden. Es lässt sich nun berechnen, welches der größte zulässige Phasenwinkel θmax für einen bestimmten Elementabstand dmax ist. Weiter oben wurde bereits als Ziel formuliert, dafür zu sorgen, dass:
für alle |m| ≥ 1 größer als 1 ist.
Hiermit kann berechnet werden, wo sich die erste Gitterkeule (m = ±1) befindet. Mit dieser Änderung und Gleichung 1 aus dem ersten Teil [5] für ∆Φ ergibt sich:
Dieser Ausdruck lässt sich wie folgt vereinfachen:
und nach dmax auflösen:
für θmax von 0 bis ±π/2
Dieses dmax ist die Bedingung dafür, dass innerhalb des eingeschränkten Scanwinkel-Bereichs θmax keine Gitterkeulen entstehen, wobei θmax kleiner als π/2 (90 °) ist. Wenn die Signalfrequenz 10 GHz beträgt und der Abstrahlwinkel um ±50 ° variiert werden soll, ohne dass Gitterkeulen entstehen, berechnet sich der maximale Abstand der Antennenelemente wie folgt:
Wird der maximale Scanwinkel eingeschränkt, so erhält man die Freiheit, den Abstand der Antennenelemente zu vergrößern, um die mechanischen Abmessungen pro Kanal zu erhöhen und die Apertur für eine vorgegebene Anzahl von Antennenelementen zu erweitern. Eine Anwendung, bei der dieses Phänomen genutzt werden kann, wäre beispielsweise eine Antenne, die in einem ziemlich schmalen Bereich abstrahlen soll. Der Elementgewinn kann für die Abstrahlung in der vorgegebenen Richtung angehoben werden und der Elementabstand lässt sich im Interesse einer größeren Apertur erhöhen. Beides resultiert innerhalb des eingeschränkten Abstrahlwinkels in einem insgesamt höheren Antennengewinn.
Gleichung 19 gibt einen maximalen Abstand von einer Wellenlänge an – auch bei einem Ablenkwinkel von null. Dies trifft zu, wenn innerhalb der sichtbaren Hemisphäre keinerlei Gitterkeulen tolerierbar sind. Im Fall eines Satelliten auf einer erdsynchronen Umlaufbahn etwa lässt sich die gesamte Erde mit einem Ablenkwinkel von 9 ° von der Mittelachse der Antenne abdecken. Möglicherweise werden sogar Gitterkeulen toleriert, solange diese nicht auf die Erdoberfläche gerichtet sind. In einer solchen Situation kann der Elementabstand mehrere Wellenlängen betragen, was zu einem noch stärker fokussierten Strahl führt.
Nicht unerwähnt bleiben sollten außerdem Antennenbauarten, bei denen versucht wird, das Problem der Gitterkeulen mit uneinheitlichen Elementabständen zu lösen. Diese Antennenarrays werden als aperiodische Arrays bezeichnet – z.B. Spiral-Arrays. Aus Gründen der mechanischen Antennenkonstruktion kann es aber wünschenswert sein, eine einheitliche Baugruppe zu haben, die sich zu einem größeren Array skalieren lässt. Dies aber würde in einem gleichförmigen Array resultieren, das den zuvor beschriebenen Bedingungen bezüglich der Gitterkeulen unterliegt.
Jobangebote+ passend zum Thema
Beam Squint
In Teil 1 [5] wurde eingangs beschrieben, wie es beim Auftreffen einer Wellenfront auf die Elemente eines Arrays abhängig von Auftreffwinkel θ der Wellenfront relativ zur Antennenachse zu einem zeitlichen Versatz zwischen den Elementen kommt. Für eine bestimmte Frequenz lässt sich eine Richtwirkung erzielen, indem der zeitliche Versatz durch eine Phasenverschiebung ersetzt wird.
Dies funktioniert bei schmalbandigen Wellenformen tatsächlich. Wenn aber die Strahllenkung bei breitbandigen Wellenformen durch Phasenverschiebung vorgenommen wird, kann der Strahl in Abhängigkeit von der Frequenz seine Richtung ändern.
Verständlich wird dies, wenn berücksichtigt wird, dass eine Zeitverzögerung eine lineare Phasenverschiebung als Funktion der Frequenz ist. Für eine bestimmte Strahlrichtung hängt somit die erforderliche Phasenverschiebung von der Frequenz ab. Umgekehrt ändert sich die Abstrahlrichtung bei vorgegebener Phasenverschiebung als Funktion der Frequenz. Das Konzept, dass sich der Abstrahlwinkel als Funktion der Frequenz ändert, wird als »Beam Squint« bezeichnet.
Bild 20
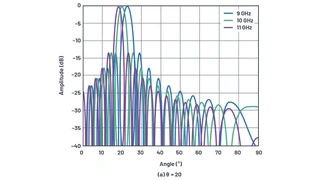
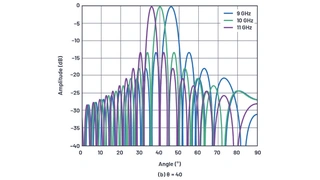
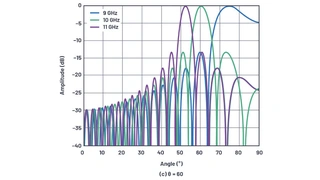
Zu beachten ist ferner, dass es in der Antennenachse mit θ = 0 zu keiner Phasenverschiebung zwischen den Antennenelementen kommt und es daher keine Möglichkeit gibt, irgendeinen Beam Squint zu erzeugen. Das Ausmaß an Beam Squint muss daher eine Funktion des Winkels θ und der Frequenzänderung sein. Bild 20 zeigt ein Beispiel für das X-Band mit einer Mittenfrequenz von 10 GHz und einer Modulationsbandbreite von 2 GHz. Darin ist klar zu erkennen, dass der Strahl als Funktion sowohl der Frequenz als auch des anfänglichen Strahlwinkels seine Richtung ändert.
Der Beam Squint lässt sich direkt berechnen. Mithilfe der Gleichungen 17 und 18 kann die Richtungsabweichung (Beam Squint) wie folgt berechnet werden:
Diese Gleichung ist in Bild 21 grafisch wiedergegeben.
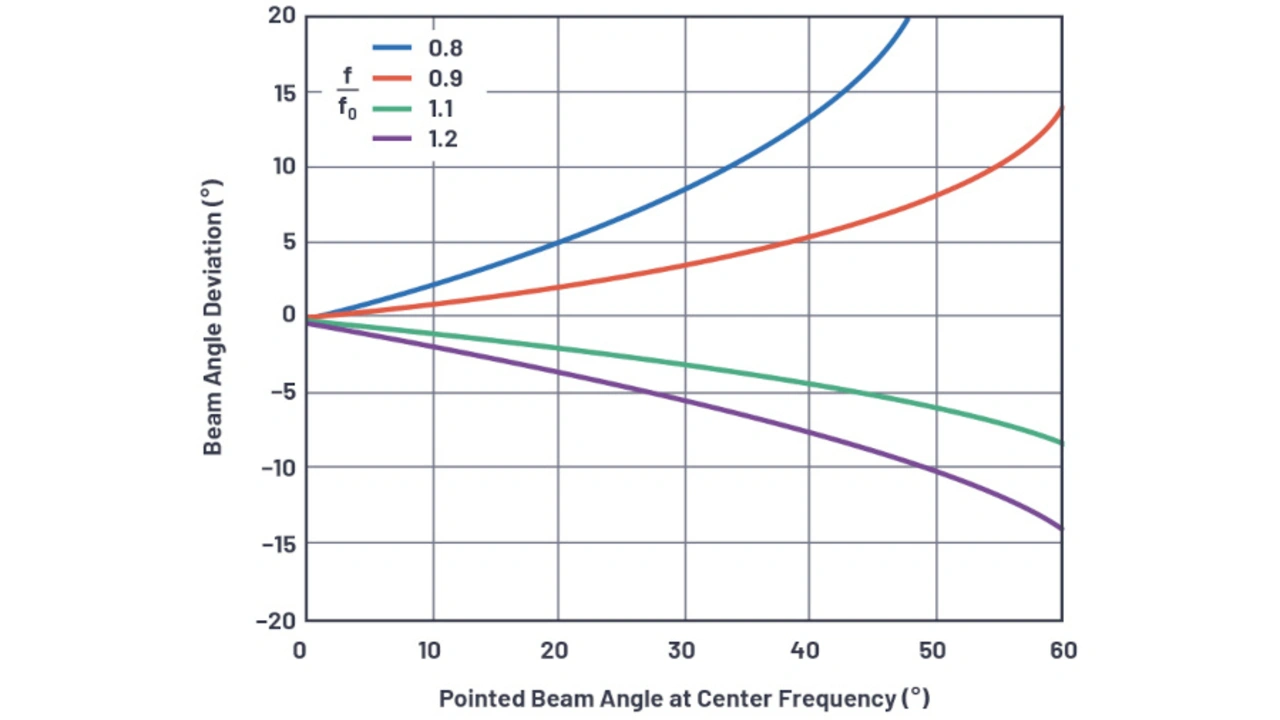
In dieser Abbildung ist mit Absicht das Verhältnis zwischen f und f0 dargestellt. Der Kehrwert des Terms f0/f aus Gleichung 29 bietet eine einfachere Möglichkeit zum Visualisieren der Änderung relativ zur Mittenfrequenz.
Es folgen noch ein paar weitere Anmerkungen zum Thema Beam Squint:
- Die Änderung des Abstrahlwinkels als Funktion der Frequenz wird umso größer, je weiter die Strahlrichtung von der Antennenachse abweicht.
- Eine Frequenz unterhalb der Mittenfrequenz bewirkt eine größere Abweichung als eine Frequenz oberhalb der Mittenfrequenz.
- Eine Frequenz unterhalb der Mittenfrequenz lässt den Strahl weiter von der Antennenachse abweichen.
Überlegungen zum Thema Beam Squint
Der Beam Squint, also die Abweichung der Abstrahlrichtung in Abhängigkeit von der Frequenz, hat seine Ursache darin, dass versucht wird einen zeitlichen Versatz durch eine Phasenverschiebung zu approximieren. Wird die Strahllenkung dagegen mit echten Verzögerungseinheiten implementiert, tritt dieses Problem nicht auf.
Angesichts des offensichtlichen Beam-Squint-Problems wäre die Frage berechtigt, weshalb überhaupt ein Phasenschieber anstelle einer Verzögerungseinheit verwendet wird. Meist sind die Einfachheit der Schaltung und die bessere Verfügbarkeit von Phasenschieber-ICs gegenüber Verzögerungseinheiten als Gründe anzuführen. Verzögerungseinheiten werden meist als Wellenleitungen realisiert, und die benötigte Gesamtverzögerung ist eine Funktion der Aperturweite. Bis dato basieren die meisten auf dem Markt angebotenen Beamforming-ICs auf Phasenschiebern, aber es kommen auch Familien mit echten Verzögerungs-ICs auf den Markt, die sich bei Antennenarrays zunehmend durchsetzen könnten.
Beim digitalen Beamforming kann eine echte Zeitverzögerung in der DSP-Logik und in den digitalen Beamforming-Algorithmen umgesetzt werden. Ein Antennenarray, bei dem alle Elemente digitalisiert sind, eignet sich also zur Eliminierung des Beam Squint-Problems und bietet gleichzeitig ein Optimum an Flexibilität durch Programmierung. Problematisch können allerdings die Stromaufnahme, der Platzbedarf und die Kosten einer solchen digitalen Bauart sein.
Schließlich gibt es das Hybrid-Beamforming als eine Kombination aus analogem Beamforming für die Sub-Antennenarrays und digitalem Beamforming für das Antennenarray insgesamt. Hiermit kann sich eine gewisse, durchaus beachtenswerte natürliche Eindämmung des Beam-Squint-Problems ergeben. Beam Squint tritt in dem Fall nur beim Sub-Antennenarray auf, bei dem die Strahlbreite deutlich größer ist, sodass eine größere Toleranz gegenüber Abweichungen der Abstrahlrichtung besteht. Solange also der Beam Squint bei den Sub-Antennenarrays hinnehmbar ist, kann ein hybrides Beamforming-Antennenarray mit Phasenschiebern in den Sub-Antennenarrays, gefolgt von echten Verzögerungseinheiten im digitalen Beamforming realisiert werden.
Im dritten Teil wird es um das Tapering als Methode zur Reduzierung von Nebenkeulen gehen, und es wird auf die Auswirkungen des Quantisierungsrauschens der Phasenschieber eingegangen.
Literatur
[1] Balanis, C. A.: Antenna Theory Analysis and Design. Dritte Auflage, John Wiley & Sons, 2005, ISBN 0-471-66782-X.
[2] Mailloux, R. J.: Phased Array Antenna Handbook. Zweite Auflage, Artech House, 2005, ISBN 1-58053-689-1.
[3] O’Donnell, R. M.: Radar Systems Engineering: Introduction. IEEE Coursees, June 2012, https://ieeexplore.ieee.org/courses/details/EDP303.
[4] Skolnik, M.: Radar Handbook. Dritte Auflage, McGraw-Hill, 2008, ISBN 978-0-07-148547-0.
[5] Delos, P.; Broughton, B. und Jon Kraft, J.: Antennenarrays – Teil 1: Strahleigenschaften von linearen Antennenarrays und Arrayfaktor. elektronik.de, 9.12.2021, www.elektroniknet.de/kommunikation/wireless/strahleigenschaften-von-linearen-antennenarrays-und-arrayfaktor.192020.html.
[6] Longbrake, M.: True Time Delay Beamsteering for Radar. 2012 IEEE National Aerospace and Electronics Conference (NAECON), IEEE, 2012.
Die Autoren

Peter Delos
ist technischer Leiter in der Aerospace and Defense Group bei Analog Devices in Greensboro, NC. Er erhielt 1990 seinen B.S.E.E. vom Virginia Tech und 2004 seinen M.S.E.E. vom NJIT. Peter Delos verfügt über mehr als 25 Jahre Branchenerfahrung. Den größten Teil seiner beruflichen Laufbahn hat er mit der Entwicklung fortschrittlicher HF-/Analog-Systeme auf Leiterplatten- und IC-Ebene verbracht. Aktuell konzentriert er sich auf die Miniaturisierung von Hochleistungsempfängern, Wellenformgeneratoren und Synthesizern für phasengesteuerte Antennenarrays.
peter.delos@analog.com

Bob Broughton
ist seit 1993 bei Analog Devices und hatte bisher Positionen als Produktingenieur und IC-Entwicklungsingenieur inne. Aktuell ist er Director of Engineering in der Aerospace and Defense Business Unit tätig. Bevor er zu ADI kam, arbeitete Bob Broughton bei Raytheon als HF-Entwicklungsingenieur und bei Peregrine Semiconductor als RFIC-Entwickler. Broughton schloss sein Studium 1984 an der West Virginia University mit einem B.S.E.E. ab.
bob.broughton@analog.com

Jon Kraft
ist Senior Staff FAE in Colorado und seit 13 Jahren bei Analog Devices tätig. Sein Schwerpunkt liegt auf softwaredefiniertem Funk sowie auf phasengesteuerte Radarantennenarrays für Luft- und Raumfahrt. Er erhielt seinen B.S.E.E. von Rose-Hulman und seinen M.S.E.E. von der Arizona State University. Er hält neun Patente, sechs mit Analog Devices und ein weiteres ist derzeit angemeldet.
jon.kraft@analog.com
- Strahlungsdiagramme: Gitterkeulen und Beam Squint
- Überlegungen zum Abstand der Antennenelemente