Antennenarrays – Teil 2
Strahlungsdiagramme: Gitterkeulen und Beam Squint
Mit steigenden Anforderungen hinsichtlich Bandbreite und Frequenz wächst das Interesse an Antennenarrays. Um die wesentlichen Eigenschaften und Zusammenhänge zu verstehen, muss man kein Antennenkonstrukteur sein – wie diese dreiteilige Reihe zeigt.
Im ersten Teil dieser dreiteiligen Serie über die Strahlungsdiagramme von phasengesteuerten Antennenarrays [5] ging es um das Schwenkkonzept und die Faktoren, die den Gewinn des Arrays beeinflussen. Thema des zweiten Teils sind Gitterkeulen und der so genannte Beam Squint, was vereinfacht als die Frequenzabhängigkeit des Abstrahlwinkels bezeichnet werden kann.
Da es schwierig werden kann, Gitterkeulen zu visualisieren, wird im Folgenden auf Ähnlichkeiten mit den Alias-Effekten bei Analog-Digital-Umsetzern zurückgegriffen. Gitterkeulen können so als räumliche Alias-Effekte betrachtet werden. Mit dem Begriff Beam Squint, im Wortsinn das „Schielen“ des Strahls, wird eine Defokussierung der Antenne über die Frequenz bezeichnet, wenn anstelle einer echten Zeitverzögerung eine Phasenverschiebung zum Schwenken des Strahls genutzt wird.
Jobangebote+ passend zum Thema
Was sind Gitterkeulen?
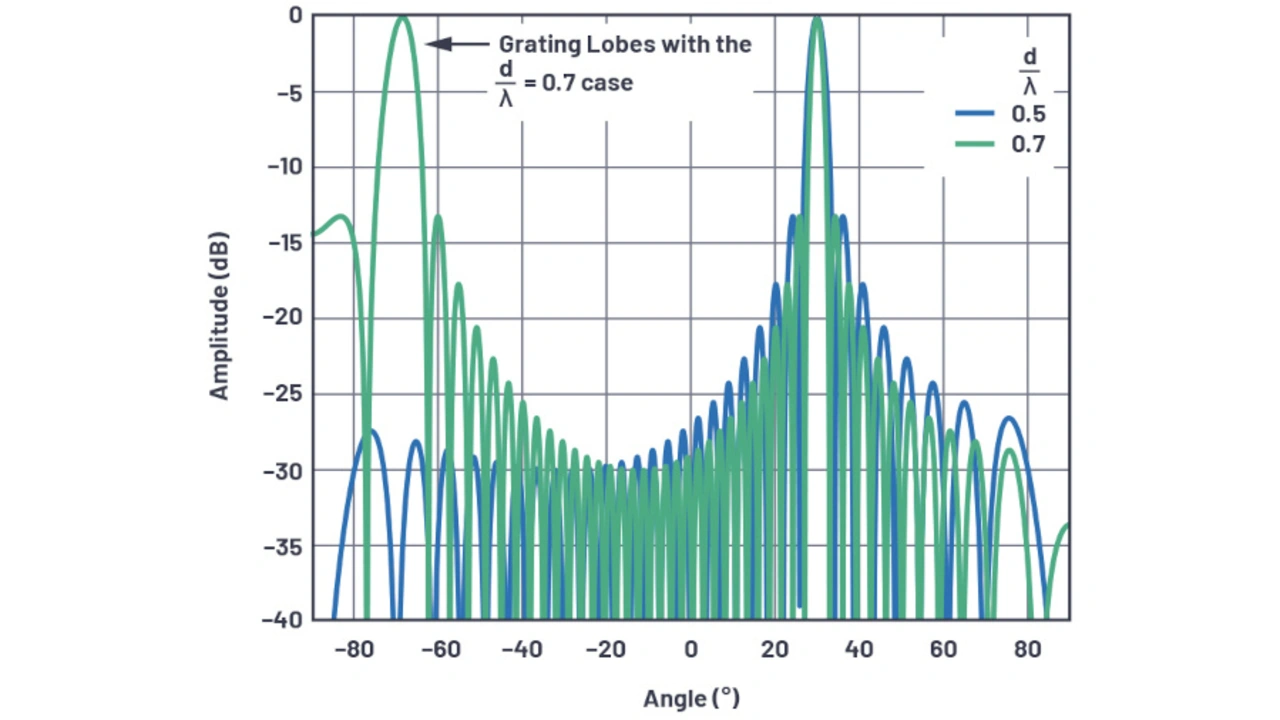
Bislang wurde ausschließlich der Fall betrachtet, dass die Antennenelemente in einem Abstand von d = λ/2 angeordnet sind. Bild 16 macht deutlich, weshalb die Platzierung der Elemente in einem Abstand von einer halben Wellenlänge bei phasengesteuerten Antennenarrays so gebräuchlich ist. Dazu sind zwei Fälle dargestellt. In blau ist wieder das 30-°-Diagramm aus Bild 11 (siehe Teil 1 [5]) dargestellt. Anschließend wird der d/λ-Abstand auf 0,7 erhöht, um zu zeigen, wie sich das Strahlungsdiagramm der Antenne hierdurch verändert.
Es ist zu erkennen, dass bei dieser Abstandserhöhung die Strahlbreite zurückgeht, was durchaus günstig ist. Auch die Tatsache, dass die Nullstellen näher zusammenrücken, ist akzeptabel. Allerdings gibt es jetzt einen zweiten Winkel, in diesem Fall –70 °, in dem sich der maximale Antennengewinn einstellt, und dies ist ein äußerst ungünstiger Effekt. Diese Replizierung des Antennengewinns wird als Gitterkeule bezeichnet und ist so etwas wie ein räumlicher Alias-Effekt.
Die Analogie zu abtastenden Systemen
Zur Visualisierung von Gitterkeulen eignet sich ein Vergleich mit den Alias-Effekten in zeitdiskreten (abtastenden) Systemen. Bei Analog-Digital-Umsetzern (ADU) wird bei der Frequenzplanung für eine Empfängerschaltung oftmals die Unterabtastung (Undersampling) zugrunde gelegt. Beim Undersampling wird die Abtastrate (fS) mit Absicht reduziert, damit Frequenzen oberhalb von fS/2 – also in den höheren Nyquist-Zonen – als Alias-Effekte in der ersten Nyquist-Zone erscheinen. Hierdurch erscheinen diese höherfrequenten Signale am ADU-Ausgang so, als hätten sie eine geringere Frequenz.
Ähnlich ist es bei phasengesteuerten Antennenarrays, bei denen die Elemente die Wellenfront in gleichen räumlichen Abständen abtasten. Das Nyquist-Theorem lässt sich auf den räumlichen Bereich anwenden, wenn angenommen wird, dass zwei Abtaststellen bzw. Elemente pro Wellenlänge erforderlich sind, um Alias-Effekte zu vermeiden. Sind also die Elemente weiter als λ/2 voneinander entfernt, kommt es zu diesen räumlichen Alias-Effekten.
Wie lässt sich die Lage der Gitterkeulen berechnen?
Wo aber kommt es zu diesen räumlichen Alias-Effekten bzw. Gitterkeulen? In Teil 1 [5] wurde untersucht, mit welcher Phasenverschiebung die Antennenelemente des Arrays angesteuert werden müssen, um den Strahl um einen bestimmten Winkel zu schwenken.
Umgekehrt lässt sich der Strahlwinkel berechnen, der sich bei einer bestimmten Phasenverschiebung einstellt:
Die Arkussinus-Funktion ergibt nur für Argumente zwischen –1 und +1 eine reelle Zahl als Lösung. Außerhalb dieses Bereichs sind die Lösungen keine reellen Zahlen. Zu beachten ist ferner, dass der Phasenwinkel in Gleichung 18 periodisch ist und sich jeweils nach 2π wiederholt. Wir können ∆Φ in der Strahlschwenk-Gleichung also durch (m × 2π + ∆Φ) ersetzen und erhalten Gleichung 19:
Darin ist m = 0, ±1, ±2, …
Um das Entstehen von Gitterkeulen zu unterbinden, darf die Gleichung nur genau eine reelle Lösung ergeben. Mathematisch ausgedrückt, müssen wir also dafür sorgen, dass gilt:
für alle m ≥ 1.
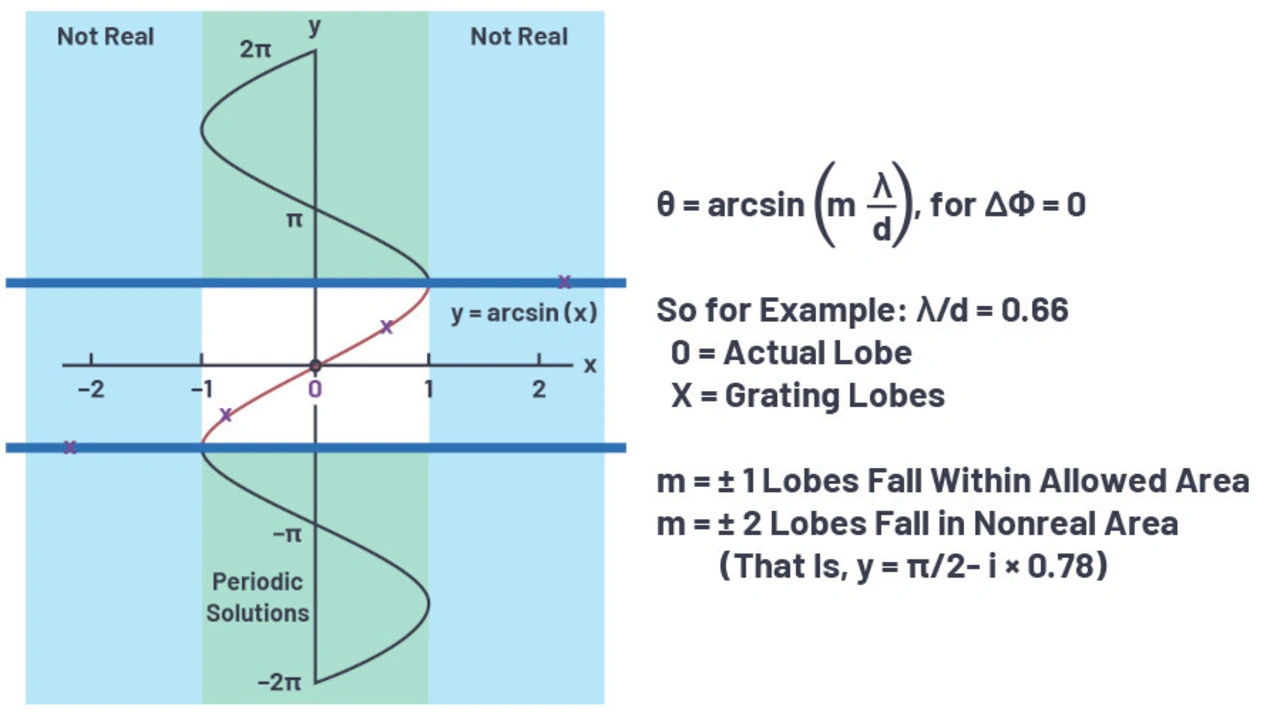
Wenn dies gemacht wird, führen alle räumlichen Abbilder – also m = ±1, ±2, usw. – bei der Arkussinus-Funktion zu nicht-reellen Ergebnissen, die ignoriert werden können. Ist dies jedoch nicht möglich, sodass einige Werte von m > 0 bei der Arkussinus-Funktion reelle Resultate liefern, ergeben sich mehrere Lösungen resp. Gitterkeulen.
Gitterkeulen für d > λ und θ = 0 °
Das gerade Gesagte soll nun an einigen Beispielen verdeutlicht werden. Zuerst sei der Fall in der mechanischen Antennenachse betrachtet, wo θ = 0 und somit ∆Φ = 0 ist. Gleichung 19 lässt sich dann zu Gleichung 21 vereinfachen:
für ∆Φ = 0
An dieser Vereinfachung wird deutlich, dass bei λ/d > 1 nur m = 0 ein zwischen –1 und +1 eingegrenztes Argument ergeben kann. Dieses Argument beträgt jedoch 0, und der Arkussinus von 0 ist 0 °, was der mechanischen Antennenachse entspricht. All dies deckt sich folglich mit unseren Erwartungen. Für jedes m ≥ 1 wird das Argument der Arkussinus-Funktion zu groß, nämlich größer als 1, sodass sich kein reelles Ergebnis ergibt. Es entstehen folglich keine Gitterkeulen für θ = 0 und d < λ.
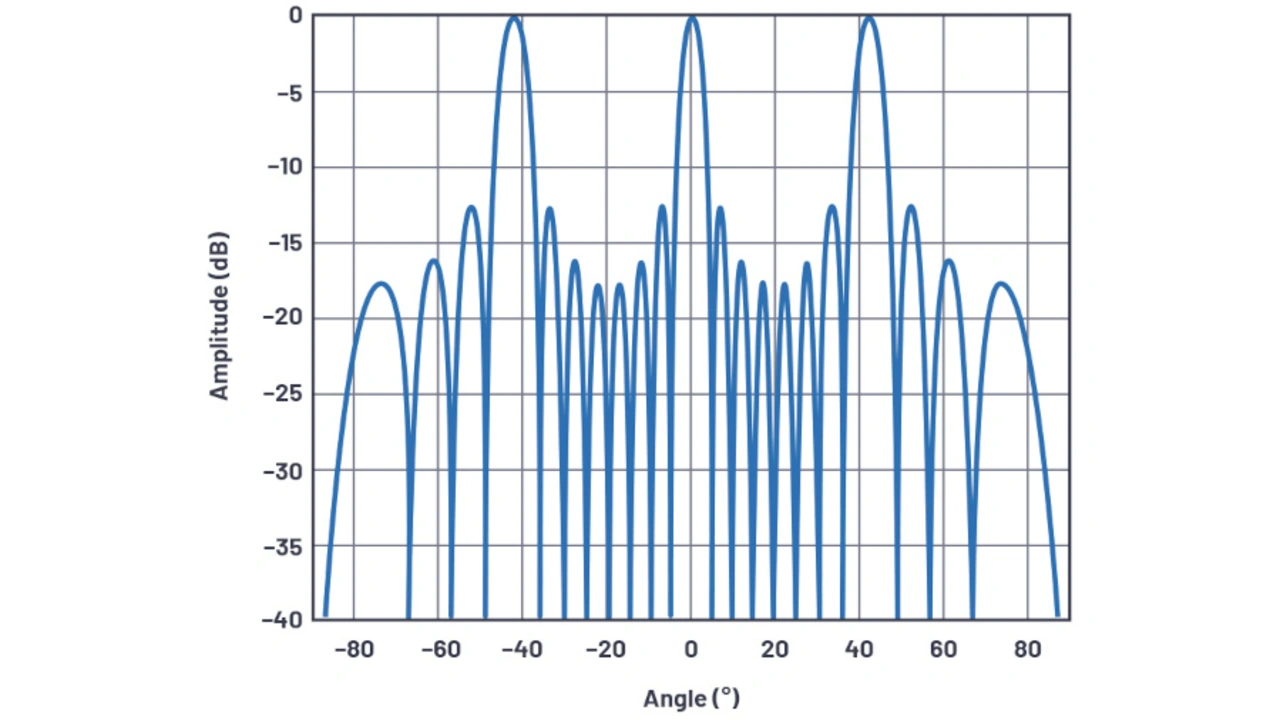
Bei d > λ (sodass λ/d < 1 ist) kann es jedoch mehrere Lösungen bzw. Gitterkeulen geben. Bei λ/d = 0,66 – d. h. bei d = 1,5∙λ – gibt es reelle Lösungen der Arkussinus-Funktion für m = 0 und m = ±1. Somit ist m = ±1 die zweite Lösung, bei der es sich um den räumlichen Alias-Effekt des eigentlich gewünschten Signals handelt. Es kann also davon ausgegangen werden, dass es drei Hauptkeulen mit nahezu gleicher Amplitude gibt, und zwar bei arcsin(0 × 0,66), arcsin(1 × 0,66) und arcsin(–1 × 0,66). In Grad ausgedrückt, betragen diese Winkel 0 ° und ±41,3 °. Genau dies lässt sich aus dem Arrayfaktor-Diagramm in Bild 18 herauslesen.
Gitterkeulen für λ/2 < d < λ
Bei der Vereinfachung der Gitterkeulen-Gleichung zu Gleichung 21 wurde festgelegt, ausschließlich die mechanische Antennenachse (∆Φ = 0) zu betrachten. Dabei wurde festgestellt, dass für d < λ keine Gitterkeulen entstehen. Aus der Analogie zur Abtasttheorie ergibt sich, dass für Abstände von mehr als λ/2 die Entstehung von Gitterkeulen irgendwelcher Art zu erwarten ist. Wo befinden sich also die Gitterkeulen für λ/2 < d < λ?
Der Blick zurück auf Bild 4 aus dem ersten Teil [5] zeigt, wie sich die Phase mit dem Abstrahlwinkel der Antenne ändert. Für einen Bereich für ∆Φ von 0 bis ±π ist zu sehen, dass die Hauptkeule von der mechanischen Antennenachse abweicht. Es gilt also für m = 0, dass:
zwischen 0 und ±0,5 × λ/d liegt.
Für |m| ≥ 1 wird dieser Ausdruck dagegen irgendwo jenseits von:
betragen.
Dies schränkt den minimal zulässigen Wert von λ/d ein, wenn sichergestellt werden soll, dass das gesamte Argument der Arcsin-Funktion für alle |m| ≥ 1 größer als 1 ist. Dabei sind zwei Fälle zu betrachten:
- Wenn λ/d ≥ 2 ist (anders ausgedrückt: d ≤ λ/2), kann es unabhängig vom Wert von m niemals mehrere Lösungen geben. Alle Lösungen mit m > 0 resultierenden in einem Arcsin-Argument über 1. Dies ist die einzige Möglichkeit, die Entstehung von Gitterkeulen zum Horizont zu unterbinden.
- Wenn dagegen ∆Φ absichtlich auf weniger als ±π begrenzt wird, können kleinere λ/d-Werte toleriert werden, ohne dass Gitterkeulen entstehen. Den Bereich von ∆Φ zu begrenzen, bedeutet aber nichts anderes als den maximalen Richtwinkel des Antennenarrays einzuschränken. Um diese interessante Abwägung geht es im nächsten Abschnitt.
- Strahlungsdiagramme: Gitterkeulen und Beam Squint
- Überlegungen zum Abstand der Antennenelemente