Antennenarrays – Teil 1
Strahleigenschaften von linearen Antennenarrays und Arrayfaktor
Mit steigenden Anforderungen hinsichtlich Bandbreite und Frequenz wächst das Interesse an Antennenarrays. Um die wesentlichen Eigenschaften und Zusammenhänge zu verstehen, muss man kein Antennenkonstrukteur sein – wie diese dreiteilige Reihe zeigt.
Aufgrund der zunehmenden Verbreitung von phasengesteuerten Antennenarrays in kommerziellen Anwendungen, in der Luft- und Raumfahrt sowie im Bereich der Wehrtechnik, beschäftigen sich immer mehr Ingenieure mit verschiedenen Aspekten der Entwicklung, obwohl sie mit den Eigenschaften von phasengesteuerten Gruppenantennen nicht vertraut sind. Die Entwicklung von phasengesteuerten Antennenarrays ist nicht neu, und die zugrundeliegende Theorie wurde über Jahrzehnte weiterentwickelt. Ein Großteil der Literatur richtet sich jedoch an Antennen-Ingenieure, die sich mit dem Thema Elektromagnetismus und der zugehörigen Mathematik gut auskennen.
Da phasengesteuerte Antennenarrays immer häufiger Mixed-Signal- und digitale ICs enthalten, könnten viele Ingenieure von einer leicht verständlichen Erklärung von phasengesteuerten Gruppenantennen profitieren. Es gibt viele Analogien zwischen dem Verhalten von phasengesteuerten Gruppenantennen und den diskreten, zeitabgetasteten Systemen, mit denen die Mixed-Signal- und Digitaltechniker täglich arbeiten.
Die drei Fachaufsätze der Antennenarray-Serie haben nicht das Ziel, Leser zu vollwertigen Antennenentwicklern weiterzubilden. Sie sollen Ingenieuren, die an einem Subsystem oder an einer Komponente arbeiten, die in einem phasengesteuerten Antennenarray verwendet wird, helfen, sich vorzustellen, wie sich ihre Arbeit auf eine phasengesteuerte Gruppenantenne auswirkt.
Jobangebote+ passend zum Thema
Strahlrichtung
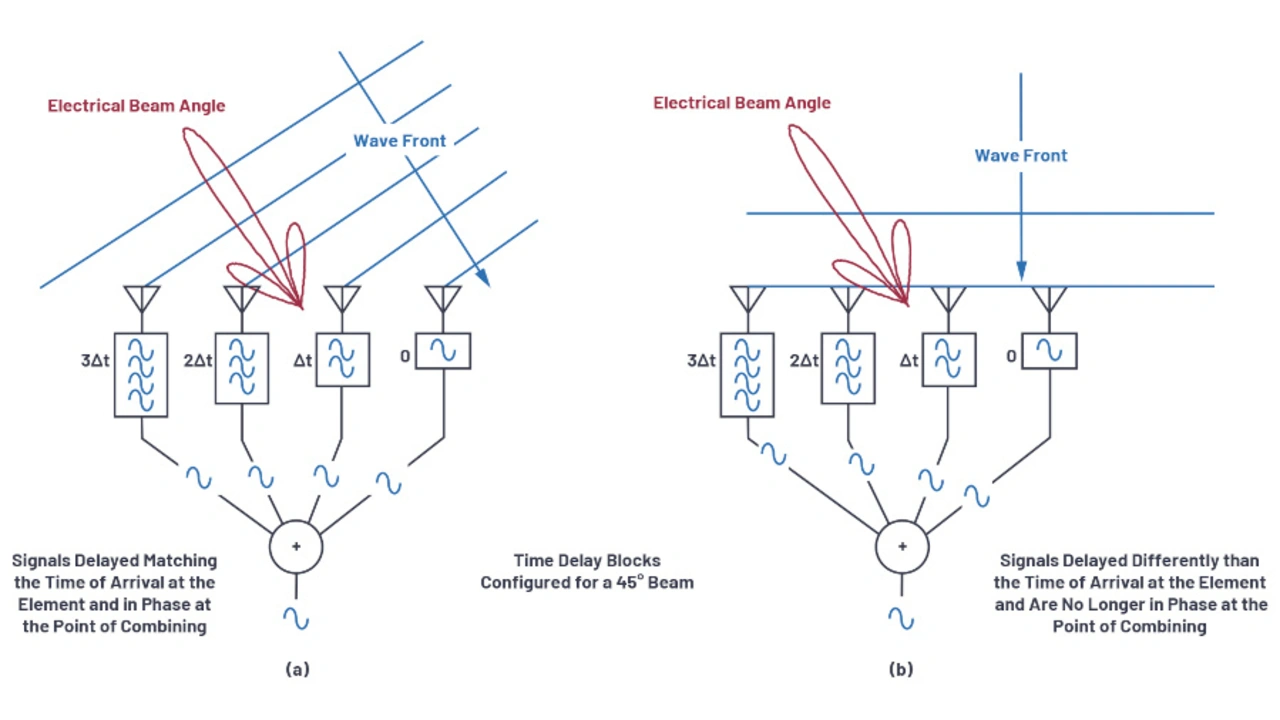
Bild 1 zeigt eine Wellenfront, die aus zwei verschiedenen Richtungen auf vier Antennenelemente trifft. Im Empfangspfad erfährt das Signal nach jedem Antennenelement eine Zeitverzögerung, bevor alle vier Signale addiert werden.
In Bild 1a entspricht diese Zeitverzögerung der Zeitdifferenz der auf jedes Element auftreffenden Wellenfront. In diesem Fall bewirkt die Verzögerung, dass die vier Signale am Summationspunkt phasengleich ankommen. Die Addition der Signale führt zu einem stärkeren Signal am Ausgang des Addierers.
Für Bild 1b gilt die gleiche Verzögerung. In diesem Fall steht die Wellenfront jedoch senkrecht zu den vier Antennenelementen. Die Verzögerung führt nun zu einer Phasenverschiebung der vier Signale, was die Leistung am Ausgang des Addierers deutlich reduziert.
In einem phasengesteuerten Antennenarray ist die Zeitverzögerung das quantifizierbare Delta, das für die Strahlsteuerung benötigt wird. Die Zeitverzögerung lässt sich aber auch mit einer Phasenverschiebung emulieren, was in vielen Implementierungen üblich und praktisch ist. Die Auswirkungen der Zeitverzögerung gegenüber der Phasenverschiebung werden im Abschnitt über den Schielwinkel (Beam Squint) diskutiert. Zunächst wird eine Implementierung mit Phasenverschiebung betrachtet und die Berechnung für die Strahllenkung mit dieser Phasenverschiebung abgeleitet.
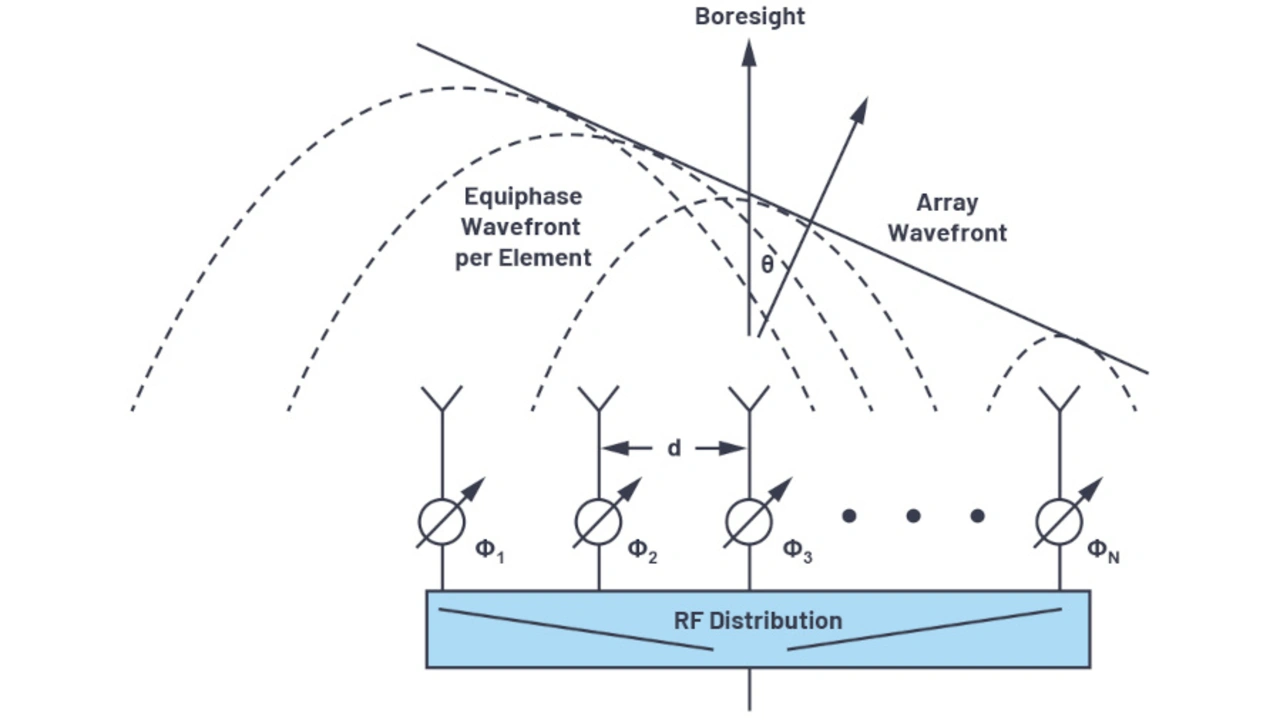
Bild 2 zeigt ein Antennenarray mit Phasenschiebern anstelle von Zeitverzögerungen. Zu beachten ist, dass die Hauptrichtung (Boresight, θ = 0°) als senkrecht zur Vorderseite der Antenne definiert wird. Ein positiver Winkel θ wird als rechts und ein negativer Winkel wird als links von der Hauptrichtung definiert.
Um die für die Strahllenkung erforderliche Phasenverschiebung zu veranschaulichen, kann ein Satz rechtwinkliger Dreiecke zwischen benachbarten Elementen gezeichnet werden (Bild 3). Dabei ist ΔΦ die Phasenverschiebung zwischen den benachbarten Elementen.
Bild 3. Ableitung der Phasenverschiebung ΔΦ
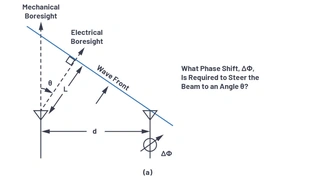
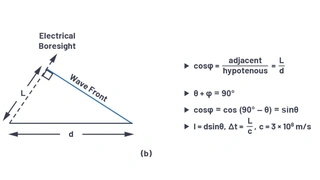
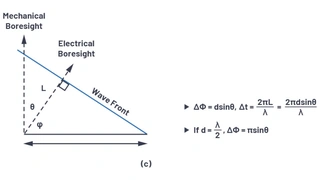
Bild 3a definiert die Trigonometrie zwischen diesen Elementen, wobei jedes Element durch einen Abstand d getrennt ist. Der Strahl wird in eine Richtung weg von der Hauptrichtung θ gerichtet, was einem Winkel φ vom Horizont aus entspricht. Bild 3b zeigt, dass die Summe von θ + φ = 90 ° ist. Dies erlaubt es, die Delta-Distanz der Wellenausbreitung L als L = dsin(θ) zu berechnen. Die Zeitverzögerung zur Steuerung des Strahls entspricht der Zeit, die die Wellenfront benötigt, um diese Entfernung L zurückzulegen. Wird L als ein Bruchteil der Wellenlänge betrachtet, dann könnte diese Zeitverzögerung durch eine Phasenverzögerung ersetzt werden. Die Gleichungen für ΔΦ können dann relativ zu θ definiert (Bild 3c) werden, wie in Gleichung 1 dargestellt.
Wenn der Abstand zwischen den Antennenelementen genau die Hälfte der Signalwellenlänge beträgt, lässt sich dies weiter vereinfachen:
Dazu ein Beispiel mit zwei Antennenelementen im Abstand von 15 mm. Wenn eine 10,6-GHz-Wellenfront in einem Winkel von 30 º zur mechanischen Ausbreitungsrichtung eintrifft, wie groß ist dann die optimale Phasenverschiebung zwischen den beiden Antennenelementen?
Wenn also die Wellenfront bei θ = 30 º eintrifft, dann bewirkt eine Verschiebung der Phase zum benachbarten Antennenelement um 95 º, dass sich die Einzelsignale beider Elemente kohärent addieren. Dadurch wird der Antennengewinn in dieser Richtung maximiert.
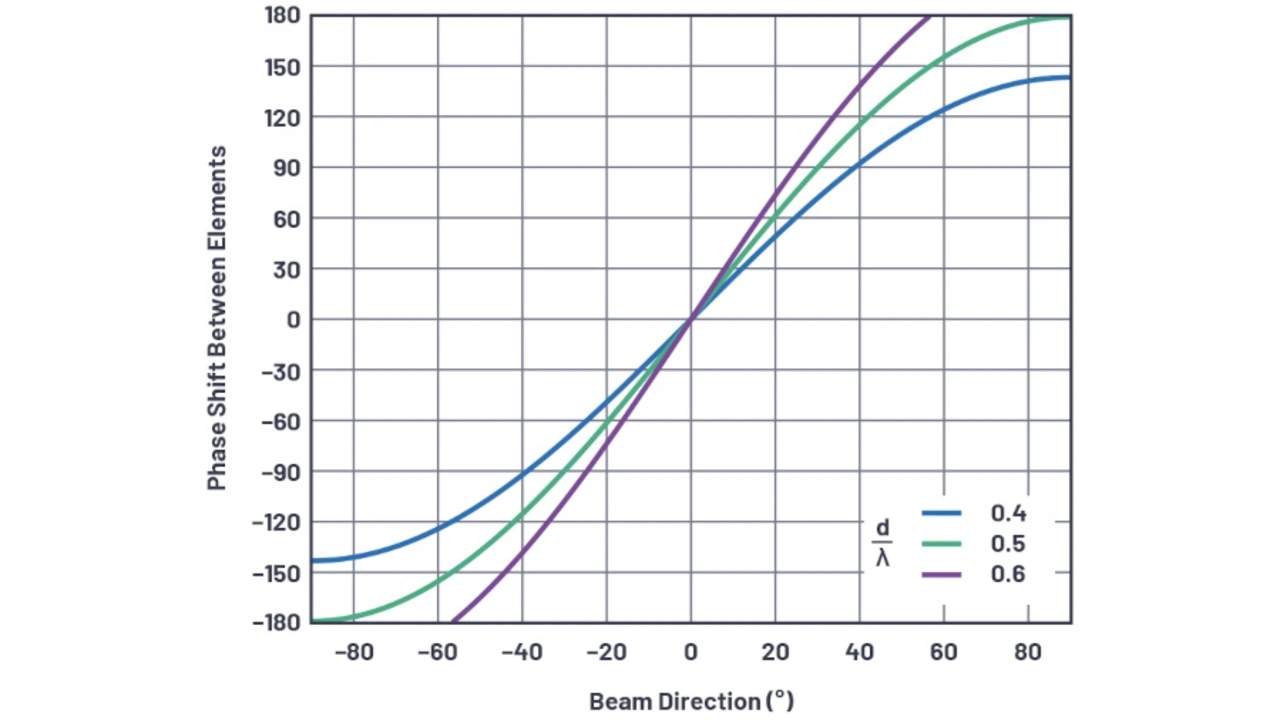
Zum besseren Verständnis, wie sich die Phasenverschiebung mit der Strahlrichtung (θ) verändert, sind die Gleichungen in Bild 4 für eine Vielzahl von Bedingungen dargestellt. Aus den Diagrammen lassen sich interessante Beobachtungen ableiten. Für den Fall von d = λ/2 gibt es eine ungefähre Steigung von etwa 3 zu 1 in der Nähe der Ausbreitungsrichtung, was dem Multiplikator von π in Gleichung 2 entspricht. Dieser Fall zeigt auch, dass eine vollständige Phasenverschiebung um 180 ° zwischen den Antennenelementen eine theoretische Verschiebung von 90 ° in der Strahlrichtung ergibt.
In der Praxis ist dies bei realen Gruppenantennen nicht realisierbar. Dennoch zeigen die Gleichungen das theoretische Ideal. Man beachte, dass für d > λ/2 kein Betrag der Phasenverschiebung eine 90 ° Strahlverschiebung ermöglicht. Später wird gezeigt, dass dieser Fall zu Gitterkeulen im Antennendiagramm führen kann, und dieses Diagramm liefert einen ersten Hinweis darauf, dass im Fall d > λ/2 etwas anders ist.
- Strahleigenschaften von linearen Antennenarrays und Arrayfaktor
- Ein lineares Antennenarray mit gleichmäßigem Abstand
- Element- und Arrayfaktoren kombinieren