Antennenarrays – Teil 1
Strahleigenschaften von linearen Antennenarrays und Arrayfaktor
Fortsetzung des Artikels von Teil 1
Ein lineares Antennenarray mit gleichmäßigem Abstand
Die oben entwickelten Gleichungen beziehen sich nur auf zwei Elemente. Eine reale phasengesteuerte Gruppenantenne kann jedoch aus Tausenden Elementen bestehen, die über zwei Dimensionen verteilt sind. Im Folgenden wird jedoch nur eine Dimension betrachtet: eine lineare Anordnung.
Jobangebote+ passend zum Thema
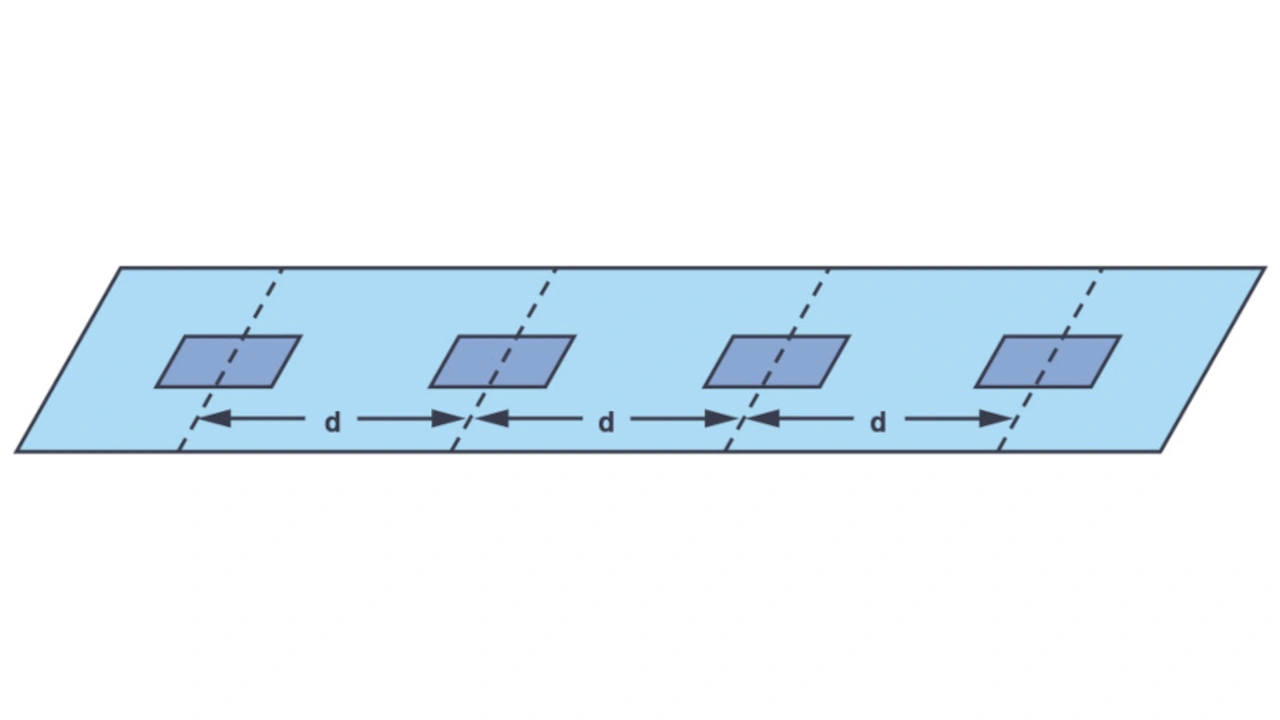
Ein lineares Antennenarray besteht aus einem einzelnen Antennenelement in der Breite und einer Anzahl von N Antennenelementen in Querrichtung. Der Abstand d kann variieren, ist aber oft einheitlich. Daher wird in diesem Beitrag der Abstand zwischen den einzelnen Elementen auf einen einheitlichen Abstand d gesetzt (Bild 5). Obwohl es sich um ein vereinfachtes Modell handelt, bietet dieses Modell eines linearen Arrays mit gleichmäßigem Abstand die Grundlage zur Erstellung des Antennendiagramms unter verschiedenen Bedingungen. Die Prinzipien des linearen Antennenarrays lassen sich weiter anwenden, um zweidimensionale Antennenarrays zu verstehen.
Nahfeld gegenüber Fernfeld
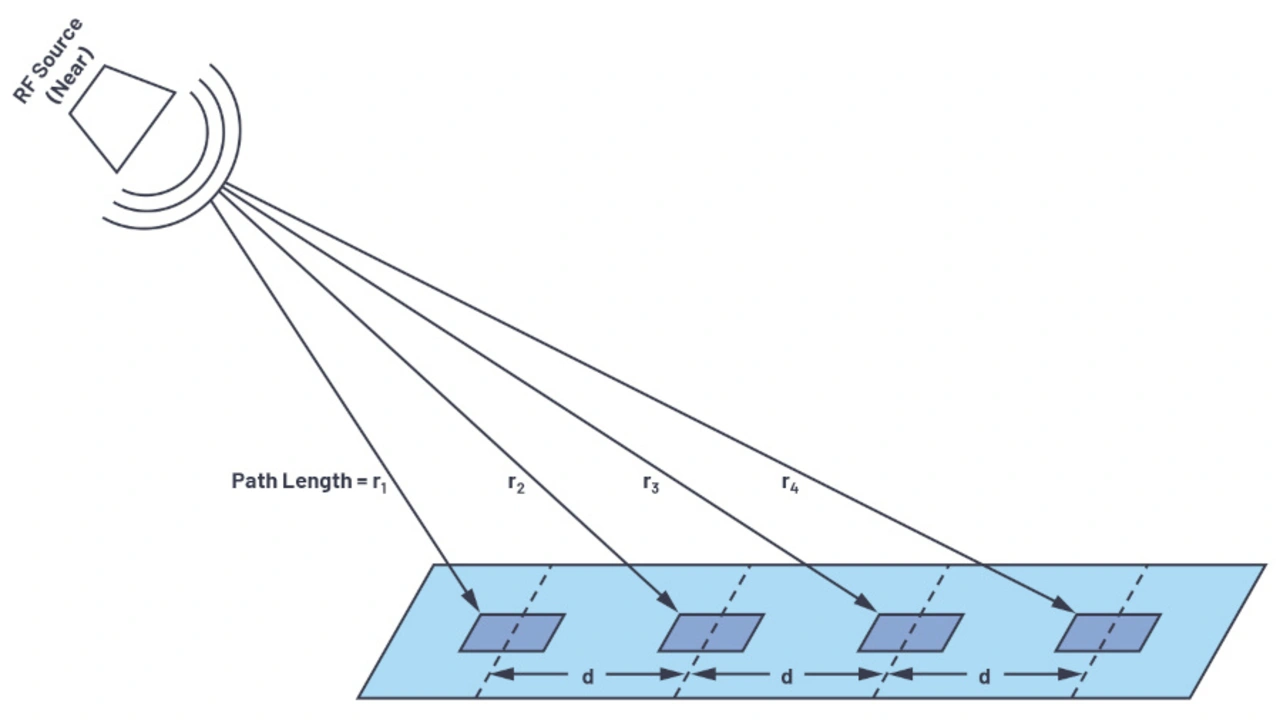
Wie lassen sich also die Gleichungen, die zuvor für eine lineare Anordnung von N = 2 entwickelt wurden, auf eine lineare Anordnung von N = 10.000 anwenden? Zunächst scheint es, dass jedes Antennenelement einen leicht unterschiedlichen Winkel hat, der auf die sphärische Wellenfront zeigt (Bild 6).
Wenn sich die HF-Quelle in der Nähe befindet, ergibt sich für jedes Element ein anderer Einfallswinkel. Diese Situation wird als Nahfeld bezeichnet. Alle Winkel können berechnet werden, und manchmal muss dies für Antennentests und Kalibrierung erfolgen, da der Testaufbau nur begrenzt groß sein kann. Ist die HF-Quelle weit entfernt, liegt der in Bild 7 gezeichnete Fall vor.
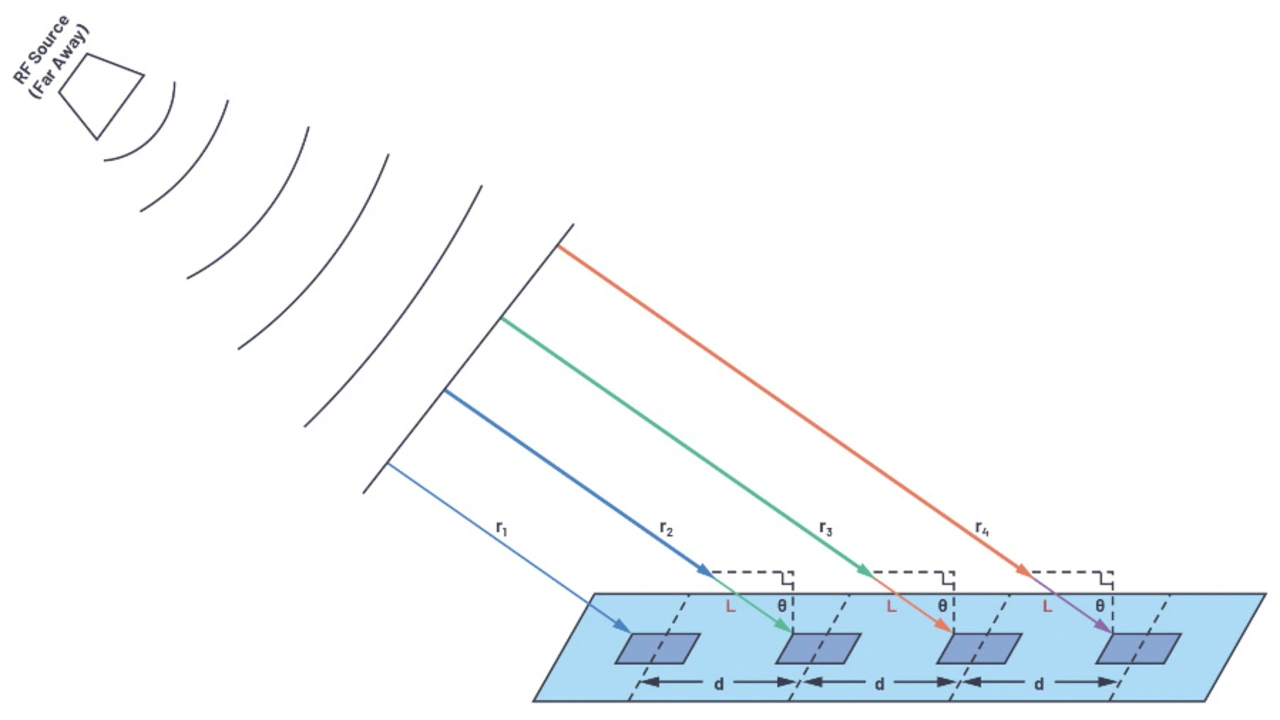
Da die HF-Quelle weit entfernt ist, führt der große Radius der sphärischen Wellenfront zu annähernd parallelen Wellenausbreitungspfaden. Daher sind alle Strahlwinkel gleich, und jedes benachbarte Element hat eine Weglänge, die L = d × sinθ länger ist als die des Nachbarelements. Dies vereinfacht die Berechnung und bedeutet, dass die beiden abgeleiteten Elementgleichungen auf Tausende Elemente angewendet werden können, sofern diese einen einheitlichen Abstand haben.
Doch wann kann die Fernfeld-Annahme gemacht werden? Wie weit ist weit? Im Allgemeinen wird als Fernfeld ein Abstand zwischen Sender und Empfänger angenommen, der größer ist als:
Darin ist D der Durchmesser der Antenne. Für ein lineares Antennenarray mit einheitlichen Abständen (d) errechnet sich D = (N-1) × d.
Für ein kleines Antennenarray (kleiner Durchmesser D) oder eine niedrige Frequenz (großes λ) ist der Fernfeldabstand klein. Für ein großes Antennenarray – oder eine hohe Frequenz – kann der Fernfeldabstand viele km betragen! Das macht es schwierig, ein Antennenarray im Labor zu testen und zu kalibrieren. Für diese Bedingungen kann ein genaueres Nahfeldmodell verwendet werden, das dann auf das Fernfeld und die reale Verwendung des Antennenarrays übertragen wird.
Antennenverstärkung, Richtwirkung und Antennenapertur
Zunächst ist es hilfreich, Antennenverstärkung, Richtwirkung und Apertur zu definieren, wobei Antennenverstärkung und Richtwirkung oft verwechselt werden. Antennenverstärkung und Richtwirkung beziehen sich auf eine isotrope Antenne – eine ideale Antenne, die gleichmäßig in alle Richtungen strahlt. Die Richtwirkung ist ein Vergleich der gemessenen Maximalleistung Pmax in einer bestimmten Richtung mit der durchschnittlichen Leistung Pmittel, die in alle Richtungen abgestrahlt wird. Wenn keine Richtung definiert ist, ergibt sich die Richtwirkung aus Gleichung 5.
Die Richtwirkung ist eine nützliche Metrik beim Vergleich von Antennen, da sie die Fähigkeit zur Fokussierung der abgestrahlten Energie definiert. Der Antennengewinn hat das gleiche Richtdiagramm, doch der Gewinn schließt die Antennenverluste ein.
Prad ist die gesamte abgestrahlte Leistung, Pein ist die Eingangsleistung der Antenne, und k steht für die Verluste in der Antennenabstrahlung.
Als nächstes wird ein Antennendiagramm als Funktion einer dreidimensionalen Richtung und die Richtwirkung als Funktion der Strahlbreite betrachtet.
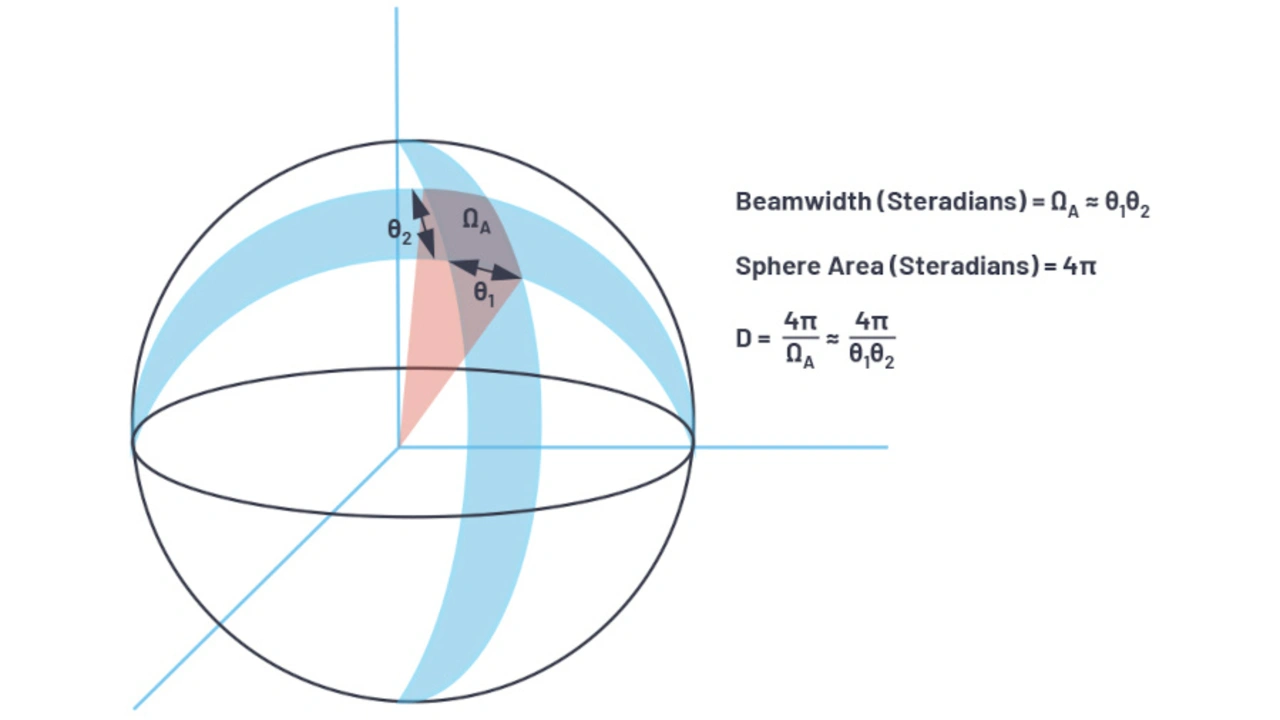
Die Oberfläche einer Kugel beträgt 4π2, und eine Fläche auf einer Kugel wird in Einheiten von Steradiant (sr) definiert. Daher beträgt die Leistungsdichte eines isotropen Strahlers
gemessen in W/m2.
Es gibt zwei Winkelrichtungen für eine Fläche einer Kugel. In Radarsystemen werden diese als Azimut und Elevation bezeichnet. Strahlbreiten können in Abhängigkeit von jeder Winkelrichtung als θ1 und θ2 beschrieben werden: Die Kombination erzeugt eine Fläche auf der Kugel von ΩA. Ω ist die Strahlbreite in sr und kann näherungsweise als ΩA ≈ θ1 × θ2 beschrieben werden.
Wird ΩA als ein Bereich auf der Kugel angenommen, dann kann die Richtwirkung wie folgt ausgedrückt werden:
Der dritte Antennenbegriff, der hier betrachtet wird, ist die Apertur. Die Antennenapertur stellt eine effektive Fläche für den Empfang elektromagnetischer Wellen dar und beinhaltet eine Funktion relativ zur Wellenlänge. Die Apertur einer isotropen Antenne ist:
Die Antennenverstärkung ist relativ zur isotropen Strahlung, so dass sich die effektive Apertur einer Antenne aus der folgenden Gleichung ergibt:
Anhand dieser drei Begriffe zeigt sich, dass der Antennengewinn als Funktion des Winkels betrachtet werden kann, der eine Strahlungscharakteristik definiert und den Wirkungsgrad – oder die Verluste – in der Antenne berücksichtigt.
Arrayfaktor für ein lineares Antennenarray
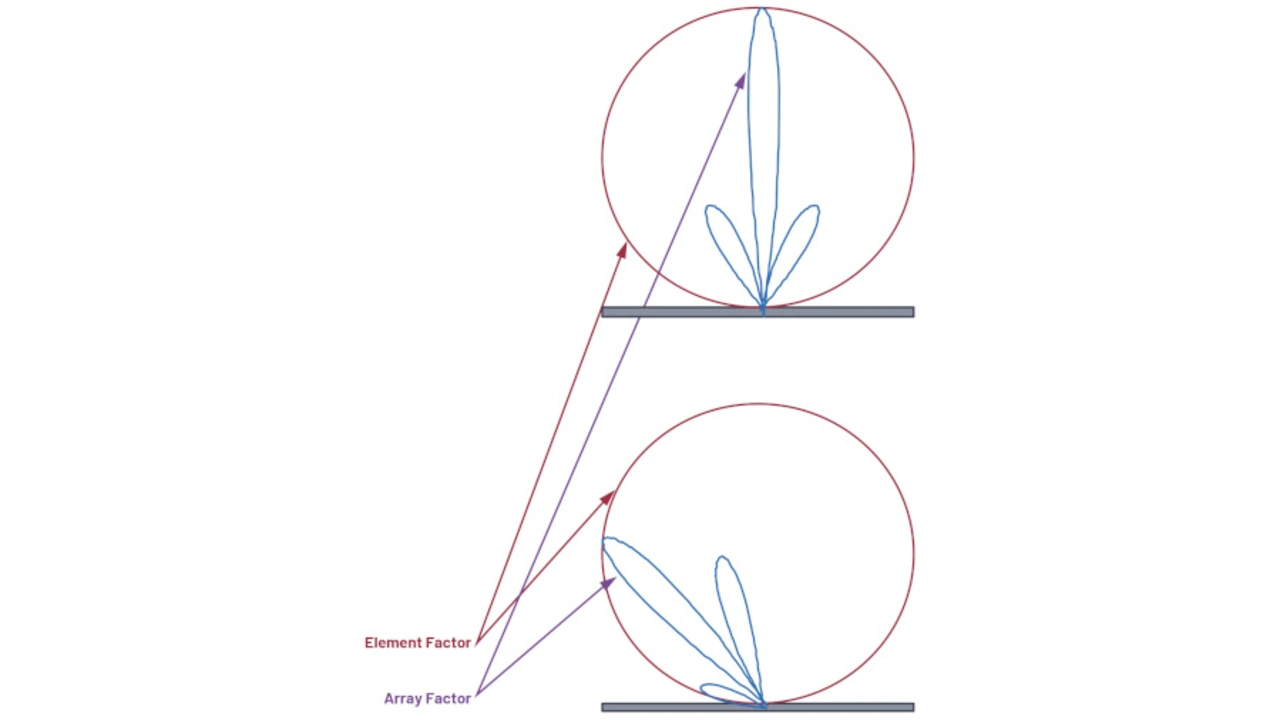
Hiermit lässt sich jetzt das optimale Delta für Zeit – oder Phase – zwischen den Antennenelementen abschätzen, um eine maximale Antennenrichtwirkung zu erreichen. Das gesamte Antennengewinndiagramm zu verstehen und zu manipulieren wäre jedoch wünschenswert. Es gibt zwei Hauptteile, um dies zu tun. Erstens gibt es die Verstärkung jedes einzelnen Antennenelements des Arrays, der als Elementfaktor (GE) bezeichnet wird. Zweitens gibt es die Wirkung, die sich durch die Strahlformung des Antennenarrays erzielen lässt, genannt Arrayfaktor (GA) (Bild 9). Das Gewinndiagramm des gesamten Antennenarrays ist die Kombination der beiden Faktoren (Gleichung 11).
Der Elementfaktor (GE) ist die Strahlungscharakteristik eines einzelnen Elements im Array. Dieser wird durch die Geometrie und Konstruktion der Antenne definiert, und nicht durch etwas, das im Betrieb variiert wird. Es ist wichtig, dies zu wissen, da es den Verstärkungsgewinn des gesamten Antennenarrays begrenzen wird – insbesondere in der Nähe des Horizonts. Da eine elektrische Steuerung nicht möglich ist, bleibt sie als fester Einflussfaktor in der gesamten Verstärkungsgleichung eines phasengesteuerten Antennenarrays. In diesem Aufsatz wird davon ausgegangen, dass alle Einzelelemente denselben Elementfaktor haben.
Der Schwerpunkt liegt dann auf dem Arrayfaktor (GA). Der Arrayfaktor wird auf Basis der Array-Geometrie – d für das einheitliche lineare Array – und der Strahlgewichte – Amplitude und Phase – berechnet. Die Ableitung des Arrayfaktors für ein einheitliches lineares Antennenarray ist einfach. Genaueres hierzu enthalten die im Literaturverzeichnis genannten Quellen.
Es gibt einige Varianten der in der Literatur verwendeten Gleichungen, je nach Definition der Parameter in der linearen Anordnung. Es werden die oben genannten Gleichungen verwendet, was eine Übereinstimmung mit den Definitionen in Bild 2 und Bild 3 ergibt. Da es hier in erster Linie darum geht, wie sich die Verstärkung ändert, ist es oft aufschlussreicher, den normierten Arrayfaktor relativ zur Einsverstärkung darzustellen. Der normierte Array-Faktor ergibt sich aus Gleichung 12.
mit θ0 = Strahlwinkel.
Der Strahlwinkel θ0 wurde bereits als Funktion der Phasenverschiebung zwischen Elementen (ΔΦ) definiert. Daher lässt sich der normierte Antennenfaktor auch mit Gleichung 13 beschreiben.
Zu den in der Gleichung für den Arrayfaktor angenommenen Bedingungen gehören:
- Die Antennenelemente haben gleiche Abstände.
- Es gibt eine gleiche Phasenverschiebung zwischen Antennenelementen.
- Die Antennenelemente haben alle die gleiche Amplitude.
Mit diesen Gleichungen lässt sich der Arrayfaktor für mehrere Array-Größen darstellten.
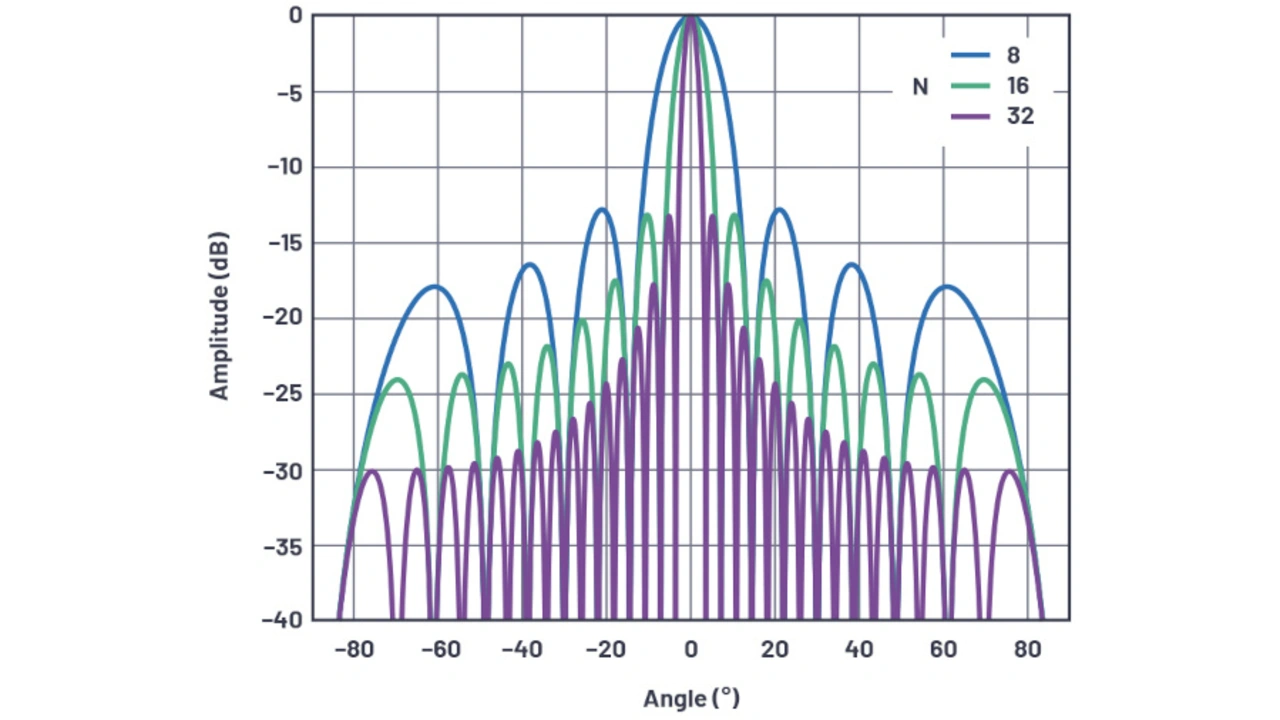
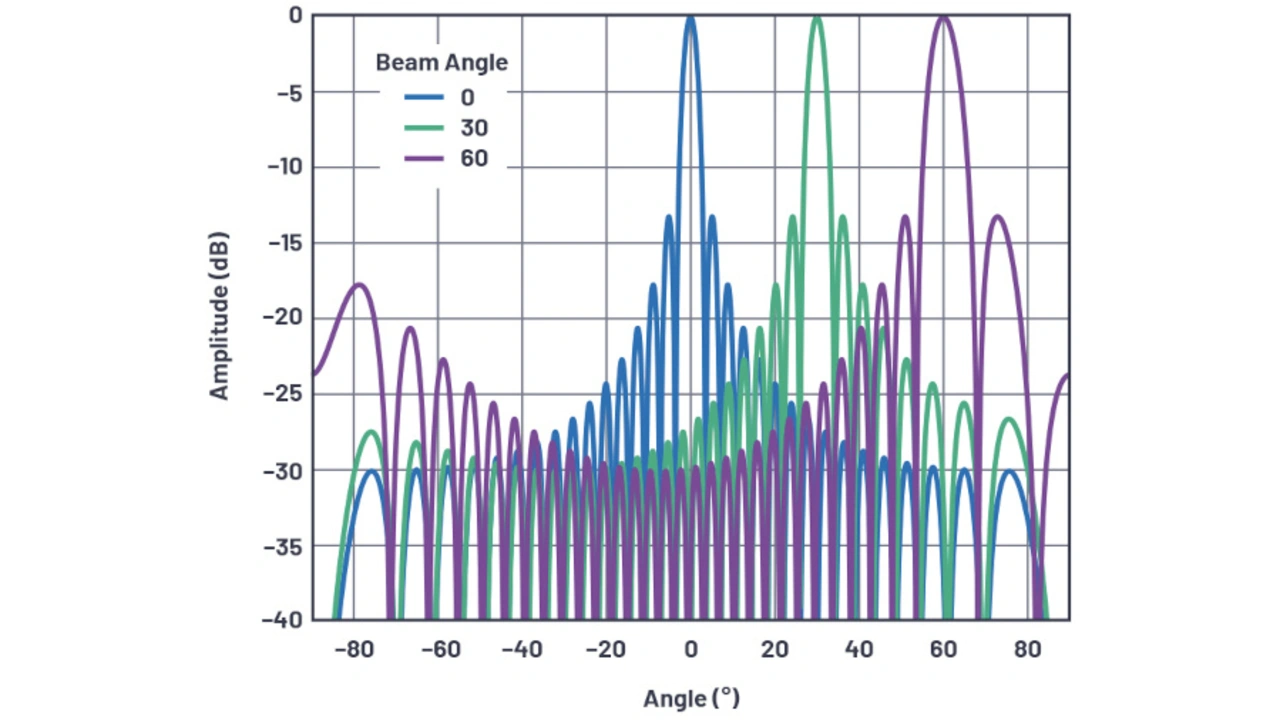
Aus diesen Zahlen lässt sich folgendes ableiten:
- Die erste Nebenkeule liegt unabhängig von der Zahl der Elemente bei –13 dBc. Dies ergibt sich aus der sinc-Funktion in der Gleichung für den Arrayfaktor. Die Nebenkeulen lassen sich durch Tapering (graduelle Gewichtung) verbessern. Beim Tapering werden verschiedene Gewinne den einzelnen Antennenelementen innerhalb des Antennenarrays zugewiesen, den Antennenelementen in der Mitte wird der höchste Gewinn zugewiesen.
- Die Strahlbreite verringert sich mit der Anzahl der Elemente.
- Die Strahlbreite vergrößert sich, wenn der Strahl von der Hauptrichtung weg abgetastet wird.
- Die Anzahl der Nullen steigt mit der Anzahl der Antennenelemente.
Strahlbreite
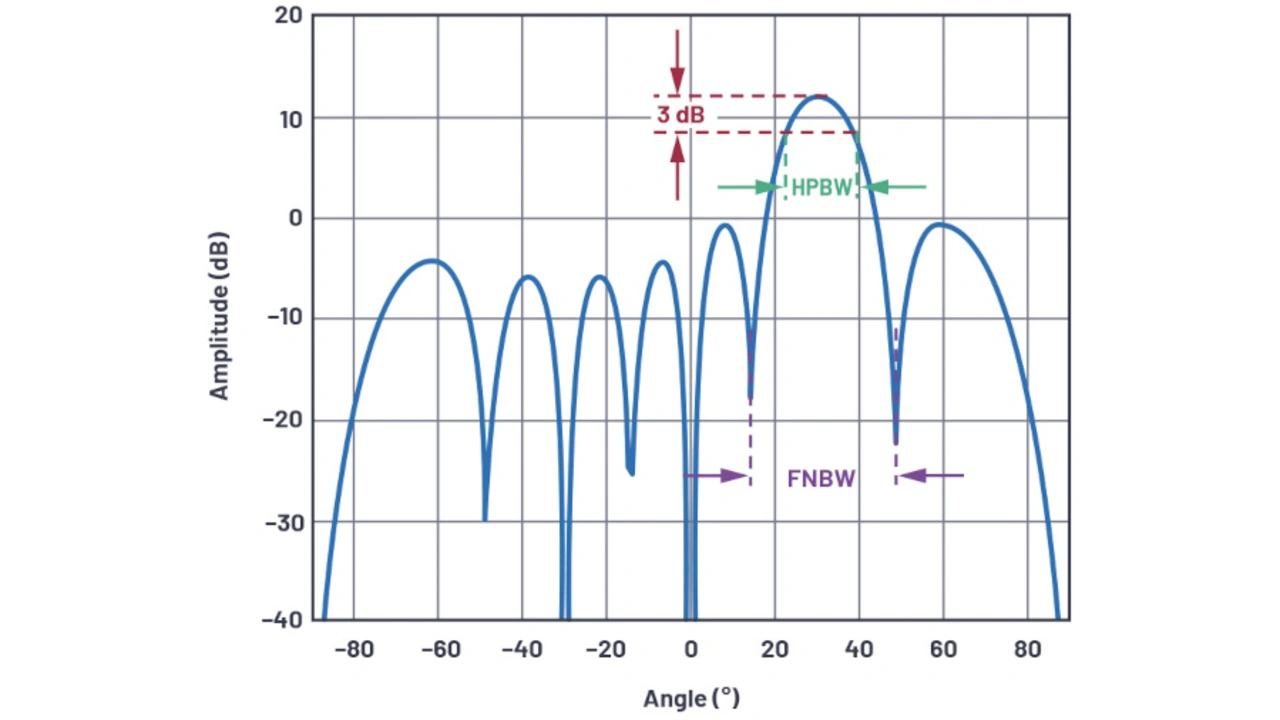
Die Strahlbreite liefert eine Metrik der Winkelauflösung für Antennen. In den meisten Fällen wird die Strahlbreite entweder durch die Strahlbreite bei halber Leistung (HPBW, half-power beamwidth) oder den Null-zu-Null-Abstand der Hauptkeule (FNBW, first null beamwidth) definiert (Bild 12). Die Strahlbreite bei halber Leistung wird ermittelt, indem in der Kurve in Bild 12 eine waagerechte Linie 3 dB unterhalb des Spitzenwertes gezogen und der Winkelabstand zwischen den Schnittpunkten gemessen wird.
Mithilfe der normierten Gleichung für den Arrayfaktor kann diese nach HPBW aufgelöst werden, indem Gleichung 4 gleich dem halben Leistungspegel – 3 dB oder 1/√2 – gesetzt wird. Als Beispiel wird eine mechanische Ausbreitungsrichtung (θ = 0º), N = 8 und d = λ/2 angenommen.
Aufgelöst nach ∆Φ ergibt sich ein Wert von 0,35 rad. Mit Gleichung 1, aufgelöst nach θ ergibt sich dann:
θ ist der Winkel von der Spitze bis zum 3-dB-Punkt, was der Hälfte der Strahlbreite bei halber Leistung entspricht. Durch Verdopplung ergibt sich der Winkelabstand zwischen den 3-dB-Punkten, ein Wert von 12,8 ° für HPBW.
Diese Berechnung könnte für einen Arrayfaktor von 0 wiederholt werden, um den ersten Null-zu-Null-Abstandswinkel von FNBW = 28,5 º für die genannten Bedingungen zu erhalten. Für gleichförmige lineare Antennenarrays ergibt sich eine Näherung für HPBW [1, 2] nach Gleichung 16.
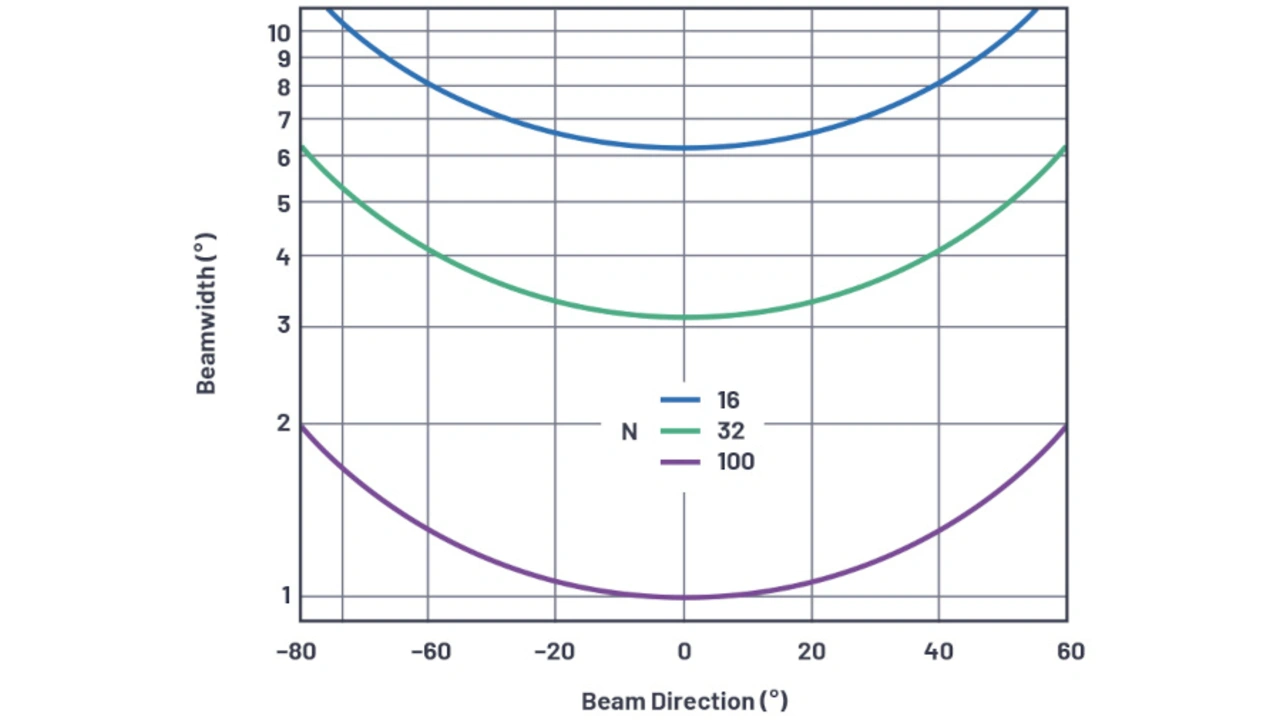
Bild 13 zeigt den Verlauf der Strahlbreite als Funktion des Strahlwinkels für mehrere Antennenelemente bei einem Abstand von λ/2 zwischen den Antennenelementen.
Aus der Grafik in Bild 13 lässt sich in Bezug auf die in der Industrie in der Entwicklung befindlichen Antennenarray-Größen folgendes ableiten:
- Für eine Strahlgenauigkeit von 1 ° sind 100 Antennenelemente erforderlich. Ist dies im Azimut und in der Elevation erwünscht, ergibt sich ein Array mit 10.000 Elementen. Die Genauigkeit von 1 ° ist nur unter nahezu idealen Bedingungen in der Ausbreitungsrichtung gegeben. Durch Beibehaltung der Genauigkeit von 1 ° im realen Betrieb über mehrere Abtastwinkel erhöht sich die Elementzahl weiter. Dies setzt dann eine praktische Grenze für die Strahlbreite bei sehr großen Arrays.
- Ein Antennenarray mit 1.000 Antennenelementen ist in der Industrie üblich. 32 Antennenelemente in jeder Richtung ergeben 1.024 Antennenelemente. So lässt sich eine Strahlgenauigkeit von weniger als 4 ° in der Nähe der Ausbreitungsrichtung erreichen.
- Ein Antennenarray mit 256 Antennenelementen, das sich kostengünstig in Massenproduktion herstellen lässt, kann immer noch eine Strahlzielgenauigkeit von weniger als 10 ° aufweisen, was in vielen Anwendungen durchaus akzeptabel sein kann.
- Zu beachten ist auch, dass sich in jedem dieser Fälle die Strahlbreite bei einem Versatz von 60 ° verdoppelt. Dies ergibt sich aus dem cosθ im Nenner und ist auf die Verkürzung des Antennenarrays zurückzuführen. Das heißt, die Arrayanordnung scheint, aus einem bestimmten Winkel betrachtet, einen kleineren Querschnitt zu haben.
- Strahleigenschaften von linearen Antennenarrays und Arrayfaktor
- Ein lineares Antennenarray mit gleichmäßigem Abstand
- Element- und Arrayfaktoren kombinieren