Antennenarrays – Teil 3
Nebenkeulen und graduelle Gewichtung
Fortsetzung des Artikels von Teil 1
Strahlwinkelauflösung vs. Quantifizierungsnebenkeulen
Eine weitere praktische Beeinträchtigung der Phased-Array-Antenne ist auf die endliche Auflösung der Zeitverzögerungseinheit bzw. des Phasenschiebers zurückzuführen, der zur Steuerung des Strahls verwendet wird. Diese Steuerung erfolgt üblicherweise digital mit diskreten Zeit- oder Phasenschritten. Wie aber werden die Auflösung oder die Anzahl der Bits bestimmt, die zum Erreichen der Strahlqualitätsziele erforderlich ist?
Entgegen einem weit verbreiteten Missverständnis ist die Strahlwinkelauflösung nicht gleich der Phasenschieberauflösung. Gleichung 30 (siehe Gleichung 18 in Teil 2 [7]) enthält diese Beziehung:
Dies lässt sich in Form der Phasenverschiebung über das gesamte Antennenarray ausdrücken, indem der Elementabstand d durch die Array-Breite D ersetzt wird. Wenn anschließend das ΦLSB des Phasenschiebers durch ∆Φ ersetzt wird, lässt sich die Auflösung des Abstrahlwinkels approximieren. Für ein lineares Antennenarray mit N Elementen im Abstand von einer halben Wellenlänge ist die Auflösung des Abstrahlwinkels in Gleichung 31 angegeben.
Dies ist die Auflösung des Abstrahlwinkels außerhalb der Hauptachse und beschreibt den Abstrahlwinkel, wenn eine Hälfte des Antennenarrays eine Phasenverschiebung von Null und die andere Hälfte eine Phasenverschiebung in Höhe des LSB des Phasenschiebers aufweist. Kleinere Winkel sind möglich, wenn weniger als die Hälfte des Antennenarrays auf das Phasen-LSB programmiert ist.
Jobangebote+ passend zum Thema
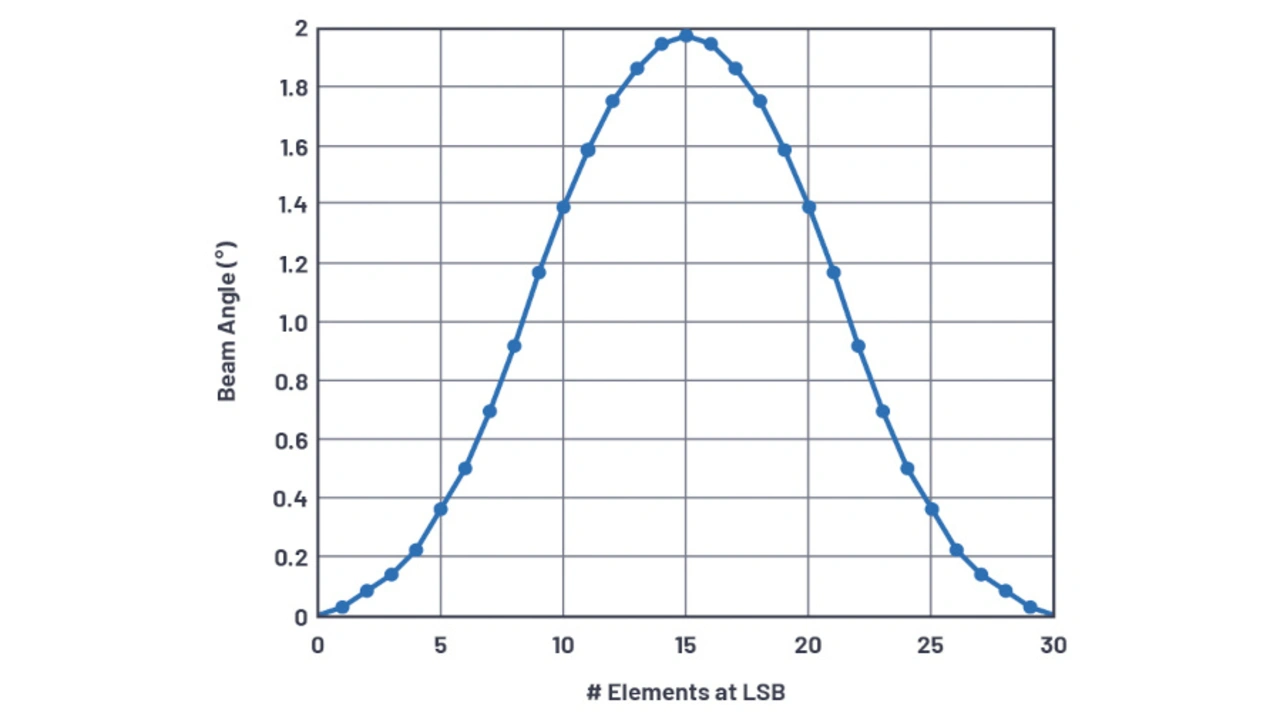
In Bild 25 ist der Abstrahlwinkel für ein Antennenarray mit 30 Elementen unter Verwendung eines 2-bit-Phasenschiebers dargestellt, während das Phasen-LSB über das Antennenarray hinweg von links nach rechts zunehmend in die Elemente geschaltet wird. Es ist zu beachten, dass der Abstrahlwinkel zunimmt, bis die Hälfte der Elemente um ein LSB verschoben ist, und anschließend wieder auf null zurückgeht, wenn sich alle Elemente am LSB befinden. Dies ist schlüssig, da sich der Abstrahlwinkel durch eine Phasendifferenz innerhalb des Antennenarrays ändert. Man beachte, dass der Spitzenwert dieser Charakteristik, wie zuvor berechnet, θRES ist.
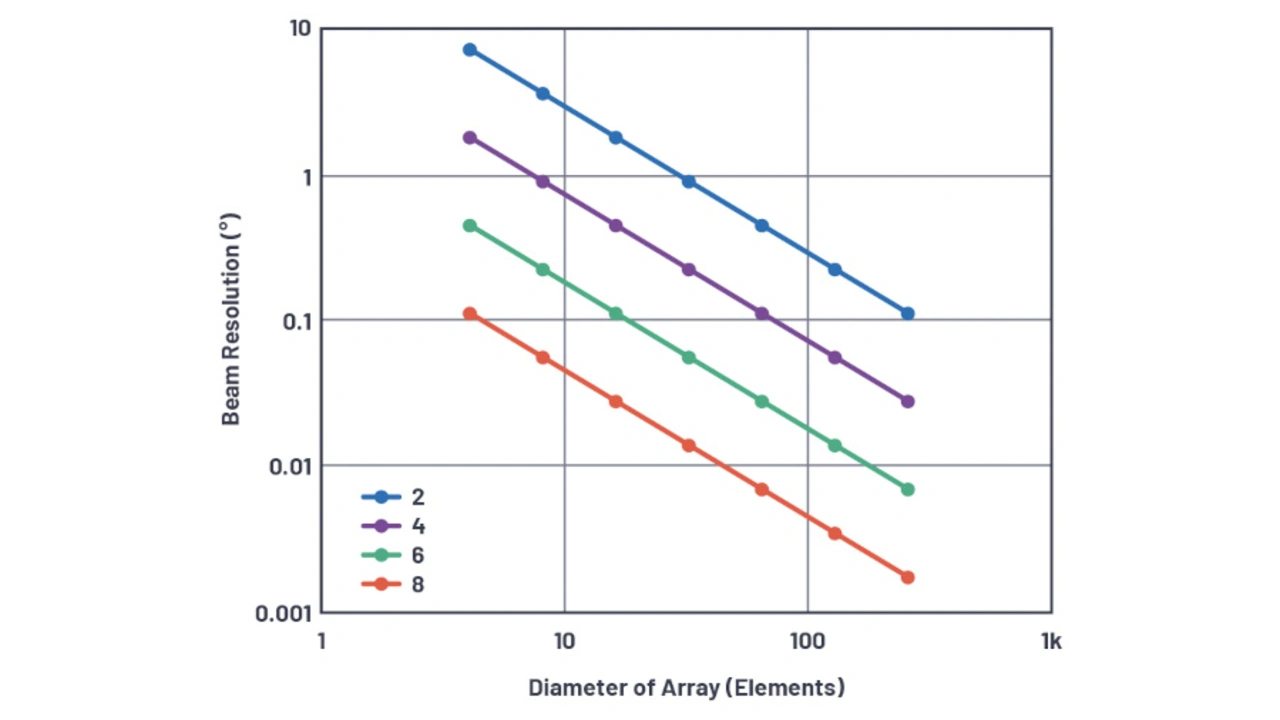
In Bild 26 ist θRES als Funktion des Array-Durchmessers (bei λ/2 Elementabstand) für verschiedene Phasenschieberauflösungen aufgetragen. Dies zeigt, dass sich sogar mit einem sehr groben 2-bit-Phasenschieber mit einem 90-°-LSB bei einem Array-Durchmesser von 30 Elementen eine Auflösung von 1 ° erreichen lässt. Bei Lösung von Gleichung 10 in Teil 1 für 30 Elemente im Abstand von λ/2 beträgt die Strahlbreite der Hauptkeule ungefähr 3,3 °, was darauf hindeutet, dass selbst mit diesem sehr groben Phasenschieber eine ausreichende Auflösung erreicht wird.
Was kann also ein Phasenschieber mit höherer Auflösung leisten? Wie sich aus Analogien zwischen zeitlich getasteten Systemen (Datenumsetzer) und räumlich getasteten Systemen (phasengesteuerte Antennenarrays) ableiten lässt, erzeugt ein Datenumsetzer mit höherer Auflösung einen niedrigeren Quantisierungsrauschpegel.
Phasen-/Zeitschieber mit höherer Auflösung führen zu niedrigeren Quantisierungs-Nebenkeulenpegeln (Quantization SideLobe Level, QSLL).
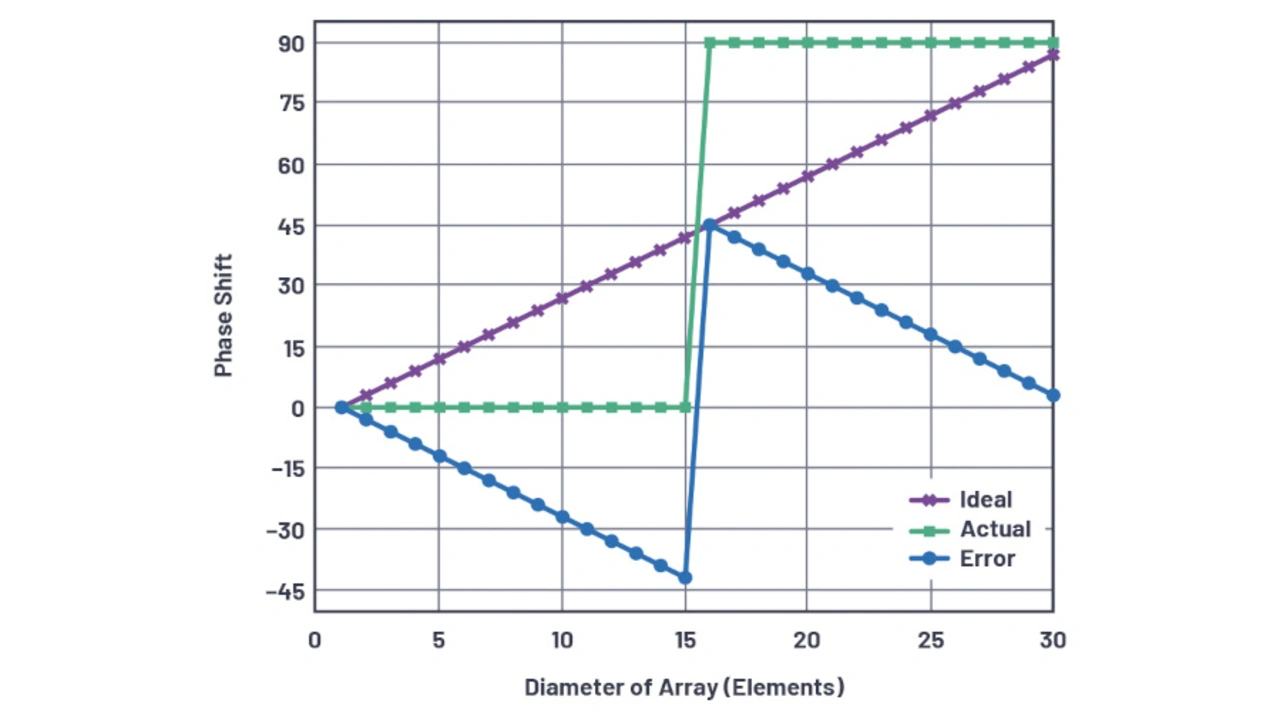
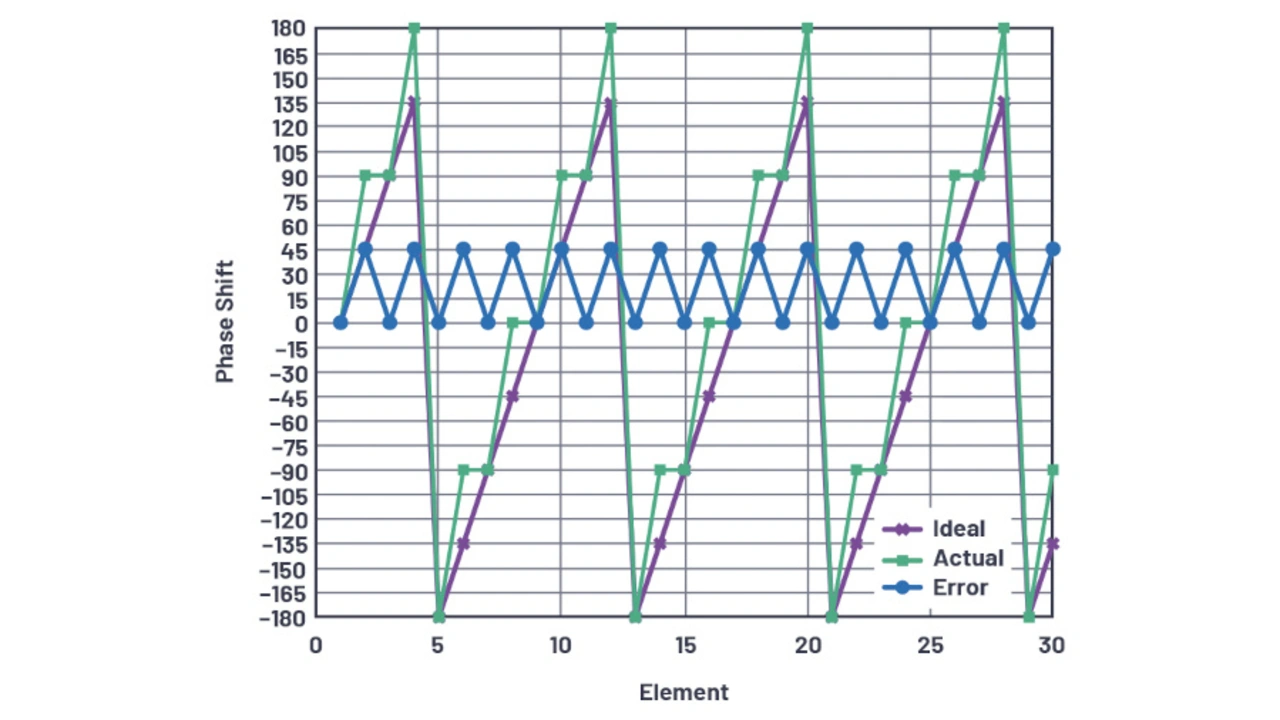
Bild 27 zeigt die Phasenschiebereinstellungen und den Phasenfehler für das zuvor beschriebene lineare 2-bit-Antennenarray mit 30 Elementen, das auf den Strahlauflösungswinkel θRES programmiert wurde. Die Hälfte des Antennenarrays ist auf eine Phasenverschiebung von Null und die andere Hälfte auf das 90°-LSB eingestellt.
Es ist zu beachten, dass der Fehler, also die Differenz zwischen der idealen und der tatsächlichen quantisierten Phasenverschiebung, sägezahnförmig ist.
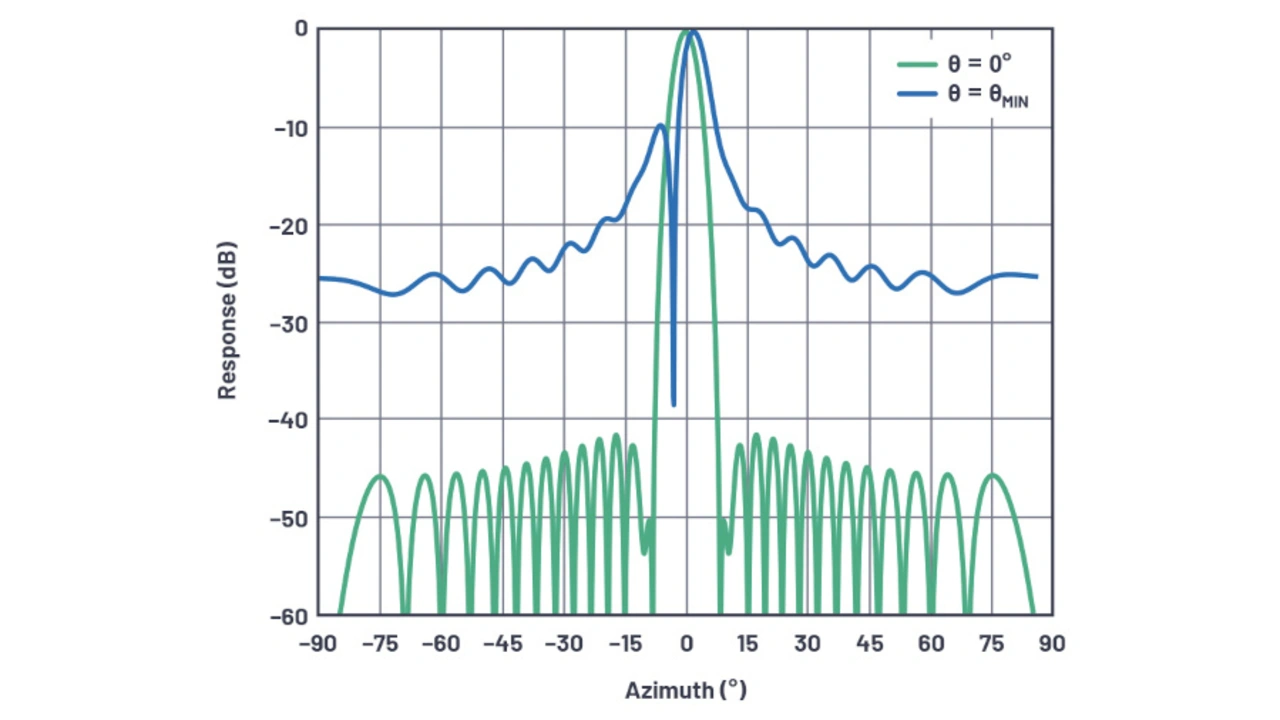
Die Antennendiagramme für dieselbe Antenne, auf 0 ° und auf den Strahlauflösungswinkel ausgerichtet, sind in Bild 28 dargestellt. Zu beachten ist, dass sich das Diagramm aufgrund des Quantisierungsfehlers des Phasenschiebers erheblich verschlechtert hat.
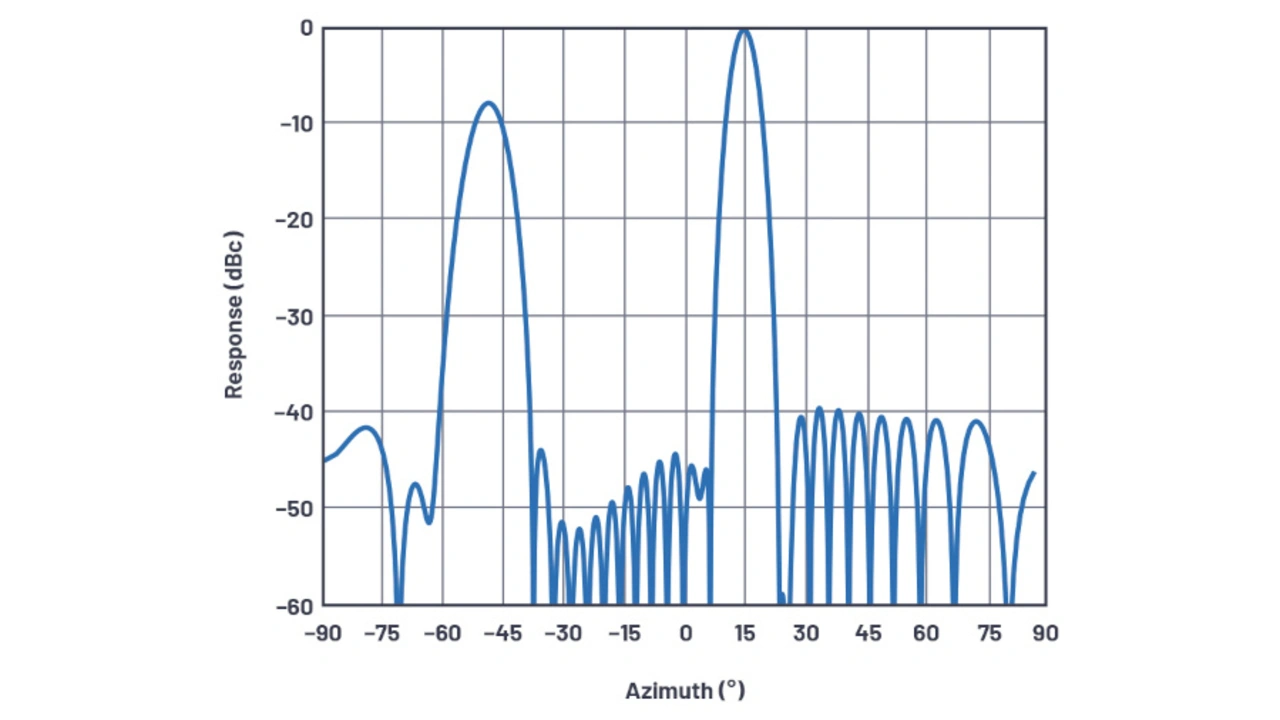
Die schlimmsten Fälle von Quantisierungsnebenkeulen treten auf, wenn der maximale Quantisierungsfehler über die Apertur hinweg auftritt, jedes zweite Element den Fehler Null hat und das Nachbarelement bei LSB/2 liegt. Dies stellt sowohl den maximal möglichen Quantisierungsfehler als auch die maximale Periodizität des Fehlers über die Apertur dar. Für den 2-bit-Fall mit 30 Antennenelementen ist diese Bedingung in Bild 29 dargestellt.
Diese Situation tritt bei vorhersehbaren Strahlwinkeln auf, wie in Gleichung 32 gezeigt ist.
Dabei ist n < 2BITS und n ungerade. Bei einem 2-bit-System ist diese Bedingung zwischen den Horizonten vier Mal erfüllt, bei ±14,5 ° und ±48,6 °. Bild 30 zeigt das Antennendiagramm für dieses System für n = 1, q = +14,5 °. Zu beachten ist die beträchtliche –7,5 dB-Quantisierungs-Seitenkeule bei –50 °.
Bei anderen Strahlwinkeln als den Sonderfällen, bei denen der Quantisierungsfehler abwechselnd 0 bzw. LSB/2 beträgt, wird der Effektivwert des Fehlers reduziert, da dieser über die Apertur verteilt wird. Tatsächlich ist der Quantisierungsfehler für die Winkelgleichung (Gleichung 32) für gerade Werte von n gleich Null.
Wenn der relative Pegel der Nebenkeule mit der höchsten Quantisierung für verschiedene Phasenschieberauflösungen aufgetragen wird, ergeben sich einige interessante Muster. Bild 30 zeigt den Worst-Case-QSLL für ein lineares Antennenarray mit 100 Elementen unter Verwendung einer Hamming-Gewichtung, so dass sich die Quantisierungsnebenkeulen von den klassischen Gewichtungsnebenkeulen unterscheiden lassen, die weiter oben in diesem Abschnitt besprochen wurden.
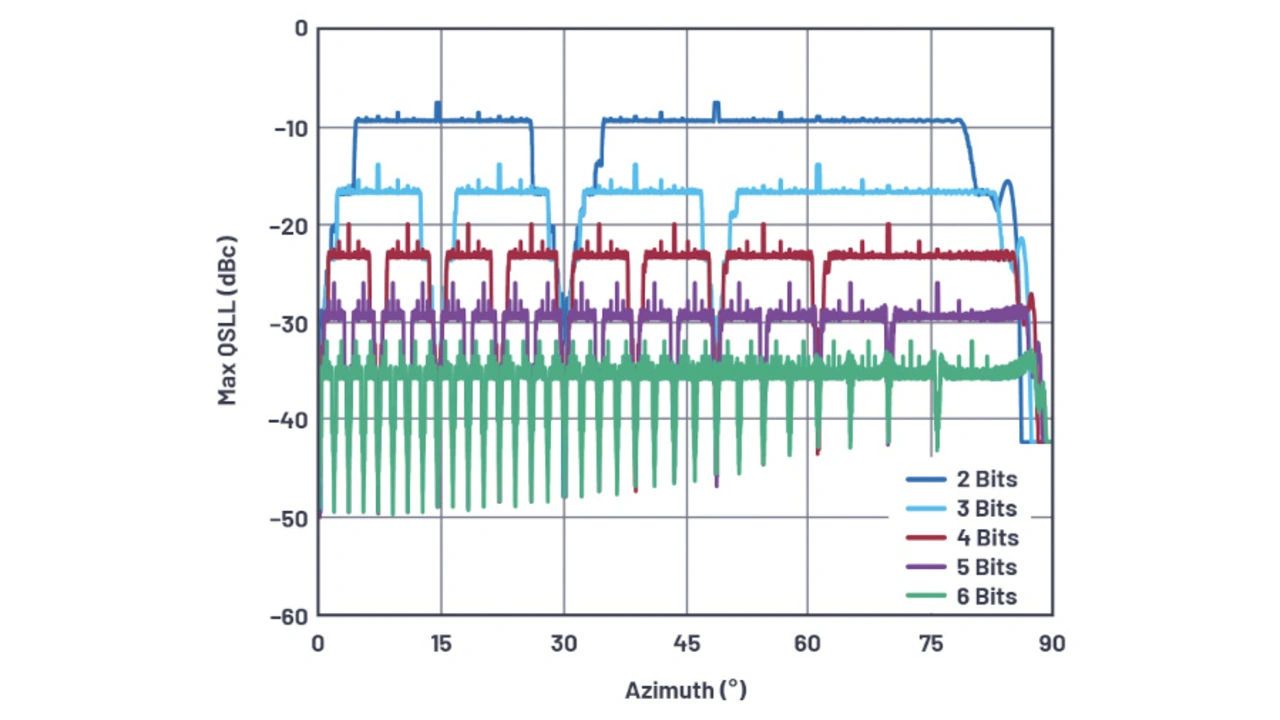
Es ist zu beachten, dass bei 30 ° alle Quantisierungsfehler zu Null werden, was nachweislich eine Folge von sin(30 °) = 0,5 ist. Zu beachten ist, dass der Abstrahlwinkel des Worst-Case-Pegels für einen bestimmten n-bit-Phasenschieber bei jeder höheren Auflösung n einen Quantisierungsfehler von Null aufweist. Die hier beschriebenen Abstrahlwinkel für Worst-Case-Nebenkeulen-Pegel sind ebenso zu sehen wie die Verbesserung des QSLL um 6 dB pro Bit Auflösung (Bild 31).
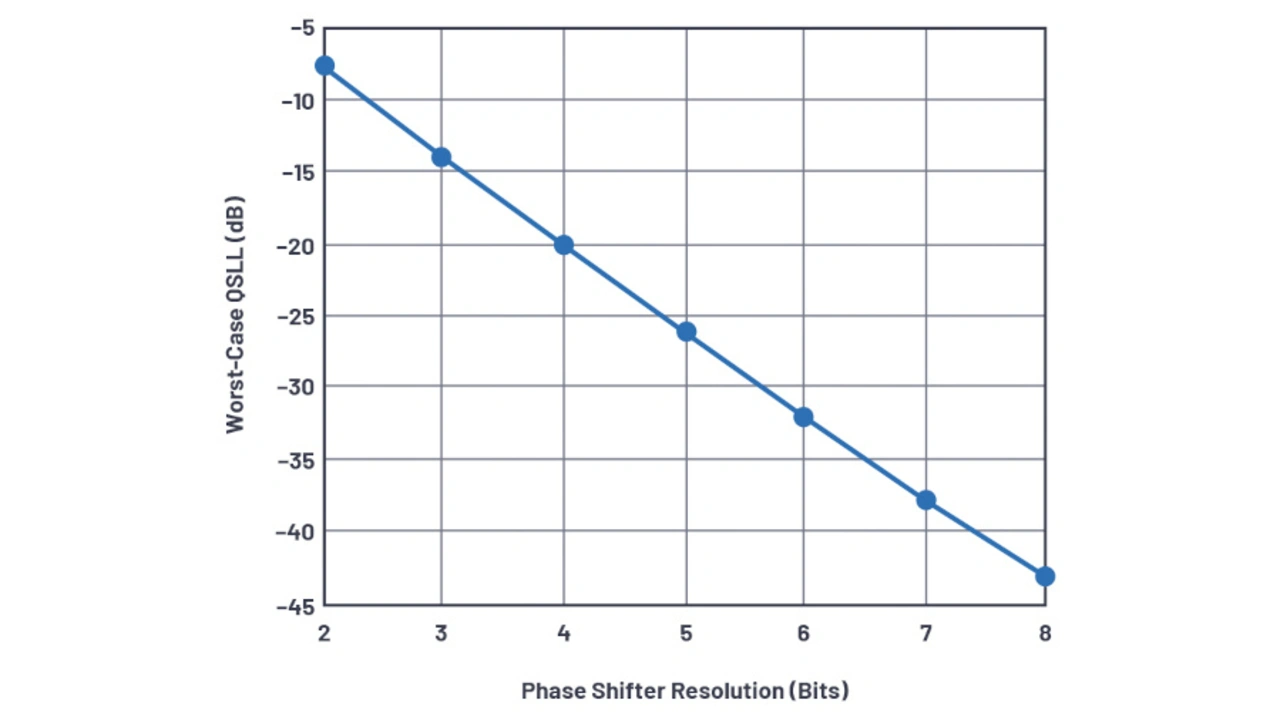
Der maximale Quantisierungsnebenkeulen-Pegel QSLL für Phasenschieberauflösungen von 2 bis 8 Bit ist in Bild 32 dargestellt, was dem bekannten Gesetz über das Quantisierungsrauschen von Datenwandlern folgt.
oder ungefähr 6 dB pro Bit Auflösung. Bei 2 bit sind die QSLL-Pegel etwa –7,5 dB und damit höher als die klassischen +12 dB für einen A/D-Umsetzer, der ein Zufallssignal abtastet. Diese Diskrepanz kann als Folge des periodisch auftretenden Sägezahnfehlers angesehen werden, der über die Apertur abgetastet wird, wobei sich die räumlichen Oberschwingungen phasengleich addieren. Zu beachten ist, dass der QSLL nicht von der Aperturgröße abhängig ist.
Zum Abschluss der Serie über Antennenarrays lassen sich einige der Herausforderungen zusammenfassen, vor denen die Antennenentwickler in Bezug auf Strahlbreite und Nebenkeulen stehen:
- Eine gute Winkelauflösung erfordert einen schmalen Strahl. Ein schmaler Strahl erfordert eine große Apertur, was viele Antennenelemente erfordert. Darüber hinaus verbreitert sich der Strahl, wenn er von der Mittelachse gesteuert wird, so dass zusätzliche Antennenelemente erforderlich sind, um die Strahlbreite bei zunehmendem Abtastwinkel beizubehalten.
- Es mag möglich erscheinen, den Abstand zwischen Antennenelementen zu vergrößern, um die Gesamtfläche der Antenne zu vergrößern, ohne zusätzliche Elemente hinzuzufügen. Dies würde den Strahl verengen, führt aber bei gleichmäßigem Abstand der Antennenelemente leider zu Gitterkeulen. Eine Reduzierung des Abtastwinkels kann zusammen mit aperiodischen Antennenarrays, bei denen ein absichtlich randomisiertes Elementmuster implementiert wird, in Betracht gezogen werden, um eine größere Antennenfläche auszunutzen und gleichzeitig das Problem der Gitterkeulen zu minimieren.
- Nebenkeulen sind ein weiteres Problem, es kann durch eine Gewichtung des Antennengewinns in Richtung der Ränder abgemildert werden kann. Die Gewichtung wird jedoch mit einer Verbreiterung des Strahls erkauft, was wiederum mehr Antennenelemente erfordert. Die Phasenschieberauflösung kann Quantisierungsnebenkeulen mit sich bringen, die ebenfalls in der Antennenkonstruktion berücksichtigt werden müssen. Bei Antennenarrays mit Phasenschiebern verursacht das Strahlschielen eine frequenzabhängige Winkelverschiebung, was für eine hohe Winkelauflösung die verfügbare Bandbreite begrenzt.
Literatur
[1] Balanis, C. A.: Antenna Theory Analysis and Design. Dritte Auflage, John Wiley & Sons, 2005, ISBN 0-471-66782-X.
[2] Mailloux, R. J.: Phased Array Antenna Handbook. Zweite Auflage, Artech House, 2005, ISBN 1-58053-689-1.
[3] O’Donnell, R. M.: Radar Systems Engineering: Introduction. IEEE Coursees, June 2012, https://ieeexplore.ieee.org/courses/details/EDP303.
[4] Skolnik, M.: Radar Handbook. Dritte Auflage, McGraw-Hill, 2008, ISBN 978-0-07-148547-0.
[5] Delos, P.; Broughton, B. und Jon Kraft, J.: Antennenarrays – Teil 1: Strahleigenschaften von linearen Antennenarrays und Arrayfaktor. elektronik.de, 9. Dezember 2021, www.elektroniknet.de/kommunikation/wireless/strahleigenschaften-von-linearen-antennenarrays-und-arrayfaktor.192020.html.
[6] Longbrake, M.: True Time Delay Beamsteering for Radar. 2012 IEEE National Aerospace and Electronics Conference (NAECON), IEEE, 2012.
[7] Delos, P.; Broughton, B. und Jon Kraft, J.: Antennenarrays – Teil 2: Strahlungsdiagramme: Gitterkeulen und Beam Squint. elektronik.de, 13. Dezember 2021, www.elektroniknet.de/kommunikation/wireless/strahlungsdiagramme-gitterkeulen-und-beam-squint.192109.html.
Die Autoren

Peter Delos
ist technischer Leiter in der Aerospace and Defense Group bei Analog Devices in Greensboro, NC. Er erhielt 1990 seinen B.S.E.E. vom Virginia Tech und 2004 seinen M.S.E.E. vom NJIT. Peter Delos verfügt über mehr als 25 Jahre Branchenerfahrung. Den größten Teil seiner beruflichen Laufbahn hat er mit der Entwicklung fortschrittlicher HF-/Analog-Systeme auf Leiterplatten- und IC-Ebene verbracht. Aktuell konzentriert er sich auf die Miniaturisierung von Hochleistungsempfängern, Wellenformgeneratoren und Synthesizern für phasengesteuerte Antennenarrays.
peter.delos@analog.com

Bob Broughton
ist seit 1993 bei Analog Devices und hatte bisher Positionen als Produktingenieur und IC-Entwicklungsingenieur inne. Aktuell ist er Director of Engineering in der Aerospace and Defense Business Unit tätig. Bevor er zu ADI kam, arbeitete Bob Broughton bei Raytheon als HF-Entwicklungsingenieur und bei Peregrine Semiconductor als RFIC-Entwickler. Broughton schloss sein Studium 1984 an der West Virginia University mit einem B.S.E.E. ab.
bob.broughton@analog.com

Jon Kraft
ist Senior Staff FAE in Colorado und seit 13 Jahren bei Analog Devices tätig. Sein Schwerpunkt liegt auf softwaredefiniertem Funk sowie auf phasengesteuerte Radarantennenarrays für Luft- und Raumfahrt. Er erhielt seinen B.S.E.E. von Rose-Hulman und seinen M.S.E.E. von der Arizona State University. Er hält neun Patente, sechs mit Analog Devices und ein weiteres ist derzeit angemeldet.
jon.kraft@analog.com
- Nebenkeulen und graduelle Gewichtung
- Strahlwinkelauflösung vs. Quantifizierungsnebenkeulen