Software-Analyse
Wertmessung statischer Tools
Statische Analysetools sind beliebt, weil sie schwere Programmierfehler finden können. Und da im Gegensatz zur dynamischen Prüfung der Code nicht ausgeführt wird, sind für diese Tools keine Testfälle notwendig, was ihrer frühen Nutzung im Entwicklungsprozess zu Gute kommt.
Mit heute verfügbaren Ressourcen ist es unvermeidbar, dass Tools nicht perfekt funktionieren: Bei der Mehrzahl der nicht-trivialen Programmen kann praktisch kein Tool alle Bugs finden (z. B. gibt es False Negatives) – und alle diese Tools könnten auch Probleme in fehlerfreiem Code melden (z. B. False Positives).
Als »Recall« bezeichnet man die Fähigkeit, echte Fehler (True Positives) aufzufinden, Recall wird definiert als Wahrscheinlichkeit, dass ein Tool einen Fehler findet. Ein Werkzeug mit 100 % Recall findet alle Fehler und gilt als zuverlässig. »Precision« hingegen ist die Fähigkeit, False Positives auszuschließen. Es bezeichnet die Wahrscheinlichkeit, dass ein Ergebnis einem echten Fehler entspricht.
Precision ist einfach messbar, sobald Warnungen die Sichtung durchlaufen haben, aber die genaue Messung des Recalls ist wegen der unbekannten Anzahl an False Negatives schwierig. Diese setzt voraus, dass man genau weiß, wie viele Fehler der zu analysierende Code enthält. Wichtig ist: Precision und Recall können in Fehlerklassen enorm variieren, sogar für ein einzelnes Tool. Ein Werkzeug, das Buffer-Overruns ausgezeichnet entdeckt, muss Resource-Leaks nicht unbedingt sehr gut auffinden.
Statische Analysetools sind so gestaltet, dass sie Ergebnisse erzielen, die in Folge eine Sichtung durch Menschen durchlaufen. Es ist möglich, die menschliche Arbeitslast durch automatisch priorisierte Warnungen je nach Risiko zu reduzieren. Ist dies einmal geschehen, bestehen die verbleibenden Warnungen aus einigen True und False Positives, die sich nur mit menschlicher Einschätzung trennen lassen.
Das Modell
Viele Faktoren tragen zur Wirtschaftlichkeit statischer Analysetools bei, und die Beziehungen zwischen ihnen sind nicht immer einfach. Als grobe Annäherung versucht das nachfolgend vorgestellte Modell, die wichtigen Aspekte des Prozesses festzuhalten. Um es nützlich und zugleich einfach zu halten, sind einige Feinheiten nicht berücksichtigt.
Die Funktion f(P) zeigt die Precision eines Tools (Wahrscheinlichkeit, dass ein True Positive korrekt erkannt wird). Die Effektivität (effectiveness) eines Tools, z. B. die Anzahl der entdeckten und als solche erkannten echten Fehler, ist demnach:
N × R × f(P)
Betrachten wir nun drei hypothetische Tools (oder Konfigurationen desselben Tools), die einen Platz im erwähnten Recall-Genauigkeitsspektrum einnehmen:
- Tool A findet Fehler einigermaßen gut mit einem Recall von 60 %. Bei der Hälfte der gemeldeten Recalls handelt es sich um False Positives.
- Tool B arbeitet mit einer Precision von 80 %, ist also sehr gut bei der Vermeidung von False Positives; aber es findet nur 30 % der echten Fehler.
- Tool C hat einen Recall von 95 %, bietet also äußerst gute Fehlerfindung, aber seine Precision beträgt nur 10 %.
Nützlich ist noch die Betrachtung von zwei anderen Fällen: Das mythische perfekte Tool, das alle Fehler ohne False Positives findet, und das Fehlen eines statischen Analysetools. Die Tabelle fasst die Eigenschaften der Tools zusammen.
Jobangebote+ passend zum Thema
| Tool A | Tool B | Tool C | No Tool | Perfect Tool | |
|---|---|---|---|---|---|
| Recall | 60 % | 30 % | 95 % | 0 % | 100 % |
| Precision | 50 % | 80 % | 10 % | 0 % | 100 % |
| Costs | USD 20.000 | USD 20.000 | USD 20.000 | 0 | 0 |
Tabelle: Eigenschaften der Beispieltools
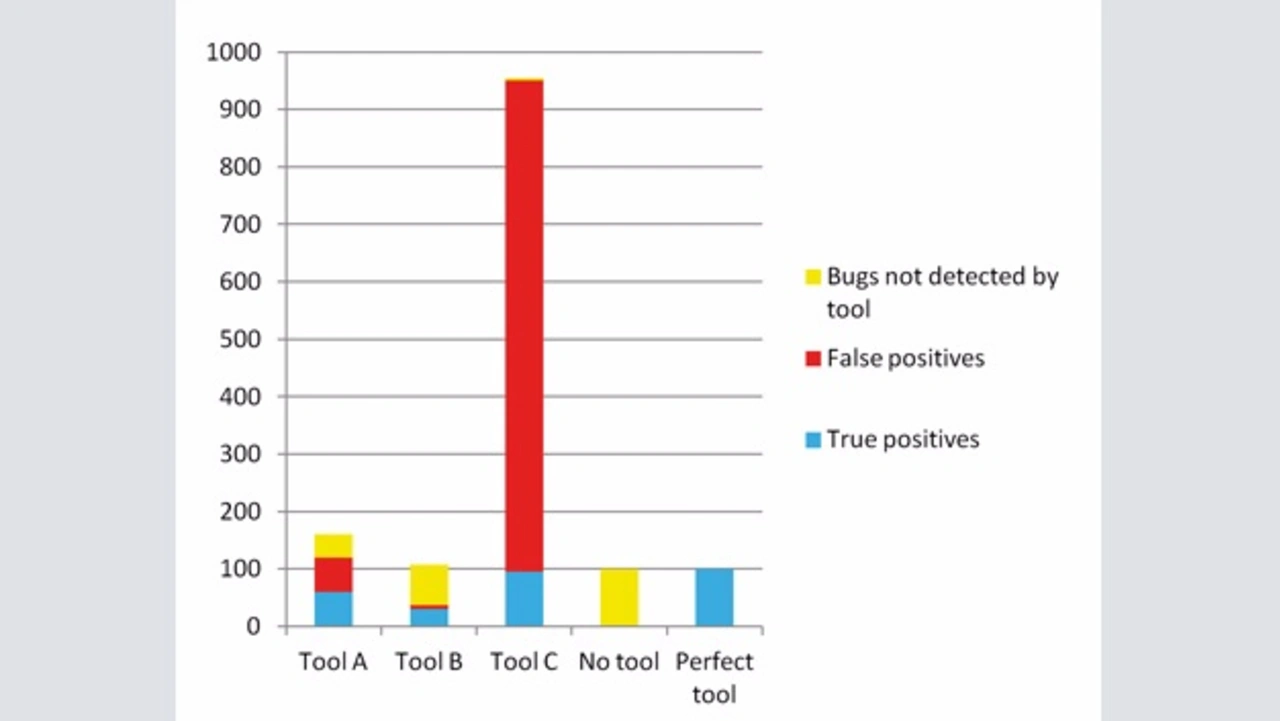
Nun nehmen wir an, dass die Anzahl der Fehler, die von anderen Methoden nicht entdeckt wurden, N=100 ist. Bild 1 zeigt die Rohergebnisse der Tools.
Entscheidend ist die Interpretation dieser Rohergebnisse: Wie erwähnt, werden einige echte Defekte nicht als solche erkannt. Bild 2 zeigt zwei Balkendiagramme der Fehler, die in der Anwendung im linearen (Bild 2a) und kubischen Modell (Bild 2b) zur Erkennung von True Positives verbleiben. Daraus ergibt sich, dass ein Sweet-Spot zwischen Precision und Recall existiert. Tool A hatte eine schlechtere Precision als Tool B und einen schlechteren Recall als Tool C, im Einsatz aber bleiben weniger Fehler in der Anwendung.
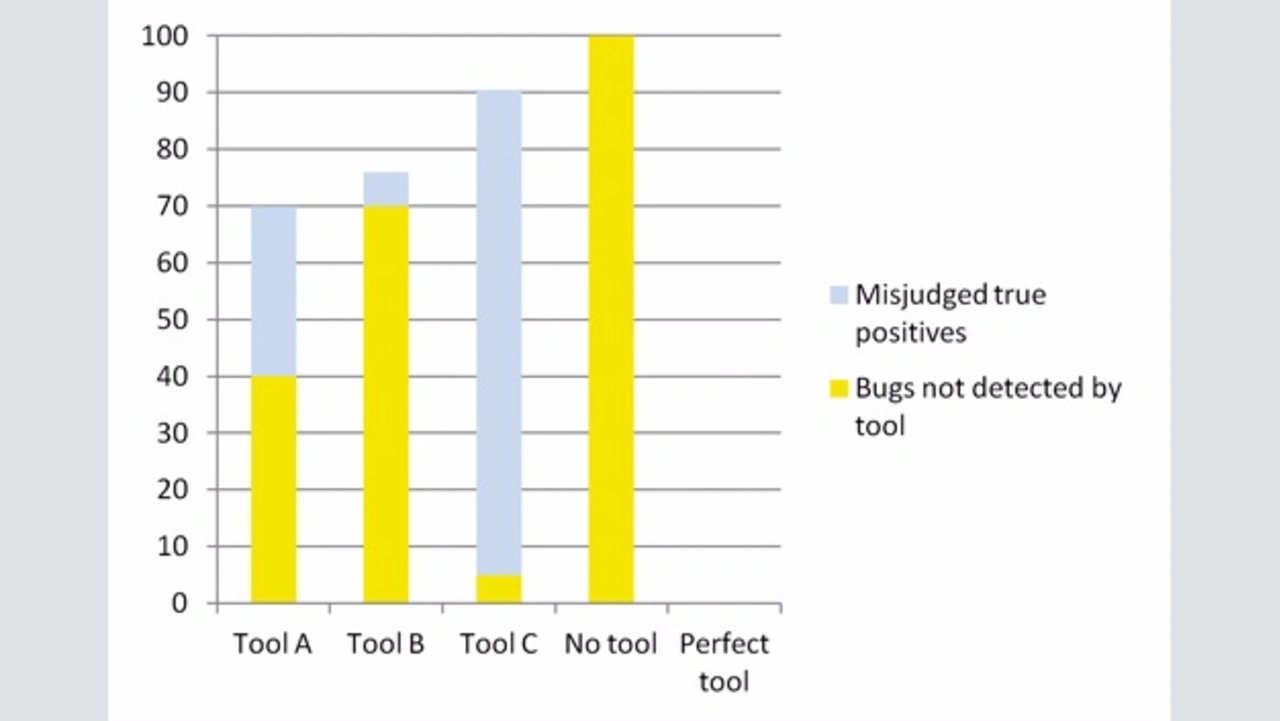
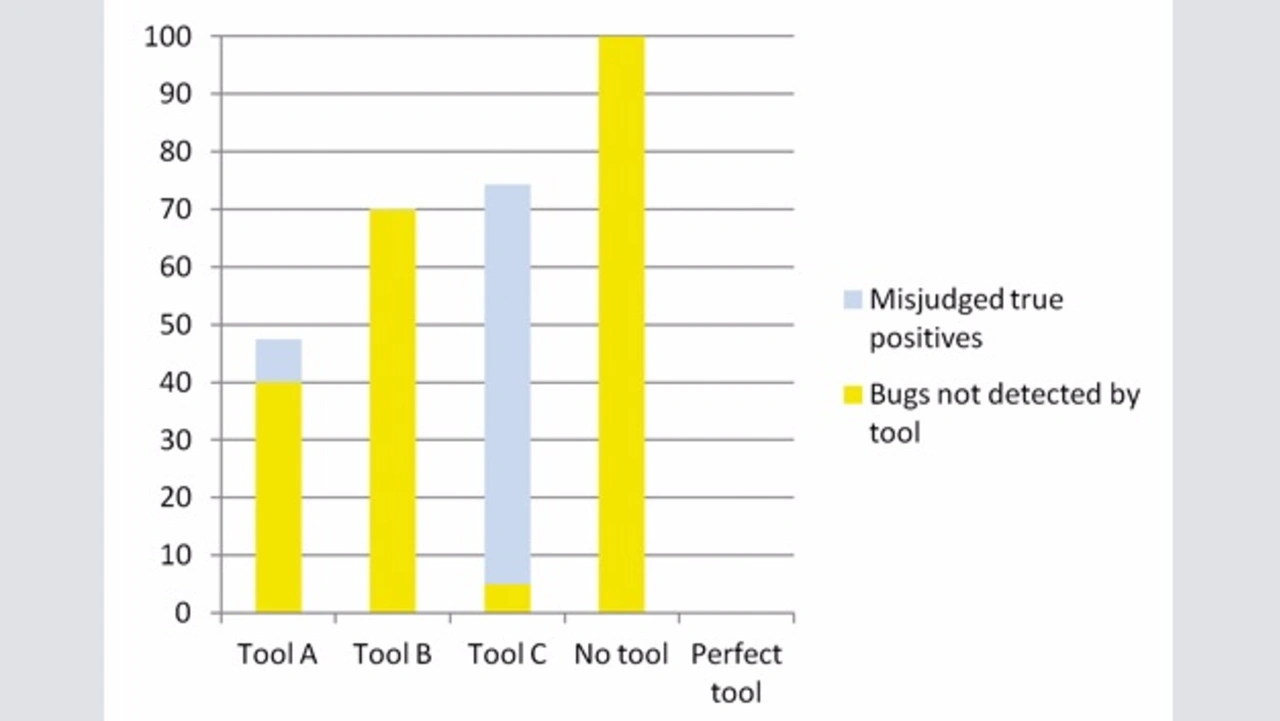
Wirtschaftlichkeit
Wichtig in Hinblick auf die wirtschaftlichen Aspekte des Prozesses sind folgende Faktoren:
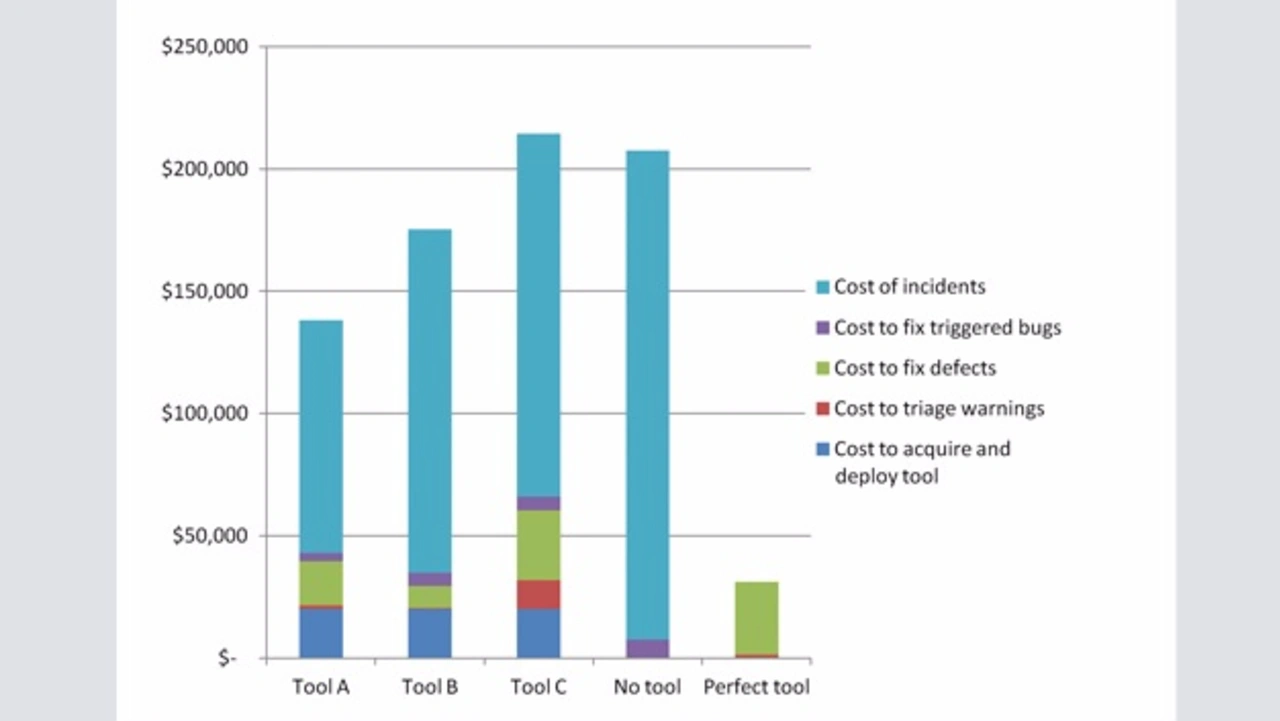
- Wahrscheinlichkeit und Kosten eines von einem Fehler hervorgerufenen Zwischenfalls: Nicht alle Software-Fehler und Sicherheits-Schwachstellen führen zu ernsten Problemen, sondern viele bleiben bis zu ihrer Entfernung im Zuge einer Routinewartung unentdeckt. Dieser Umstand lässt sich modellieren durch die Zuordnung einer Wahrscheinlichkeit, dass ein Fehler einen Zwischenfall im Lebenszyklus eines Produkts auslöst: Verursacht ein Fehler einen Zwischenfall, führt der Umgang damit zu Kosten, die enorm variieren können. Die Zahlen in Bild 3a und Bild 3b beruhen auf einer Wahrscheinlichkeit von 5 % und beispielhaften Ausgaben von 40 000 US-Dollar für den Zwischenfall.
- Die Zeit für die Fehlerkorrektur: Unabhängig davon, ob ein Fehler zu einem Zwischenfall führt, entstehen Entwicklungskosten für seine Beseitigung. Früh entdeckte Defekte sind wesentlich günstiger zu beheben als die zu einem späteren Zeitpunkt gefundenen, weil das Produkt unter Umständen neu getestet werden muss. In den unten angeführten Kalkulationen braucht es vier Stunden, um einen Fehler früh im Entwicklungszyklus zu beseitigen, gegenüber 20 Stunden für dessen Korrektur nach dem Einsatz. Die Werte entstammen einem NIST-Report von 2002.
- Die Zeit für die Sichtung von Warnungen: Die Warnmeldung eines statischen Analysetools zu sichten, ist zuweilen zeit-intensiv. Der Großteil geht schnell, aber schwierige Reports können ausführliche Passagen über den Code, mehrere Umleitungen und komplexe Beziehungen zwischen Variablen enthalten. Erfahrungsgemäß dauert eine Triage durchschnittlich zehn Minuten pro Warnung.
- Entwicklungsaufwand: Schlägt hier mit 75 US-$/Std. (einschl. Gemeinkosten) zu Buche.
- Kosten für die Tool-Entwicklung: Darin eingeschlossen sind die Ausgaben für den Kauf und den Einsatz des Tools auf dem Code. Im Modell werden die Tools A, B und C mit 20 000 US-$ angesetzt; weitere Kosten fallen nicht an.
Mit diesen Variablen als Input setzt sich der Preis für ein Tool zusammen aus dem Kaufpreis und der Bereitstellung, Engineering-Aufwand für die Sichtung des Berichts und die Behebung der gefundenen Fehler. Dazu kommen die Ausgaben für den Umgang mit Fehlern, die vom Tool nicht gefunden werden – vom Auffinden bis zur Handhabung aller ausgelösten Zwischenfälle.
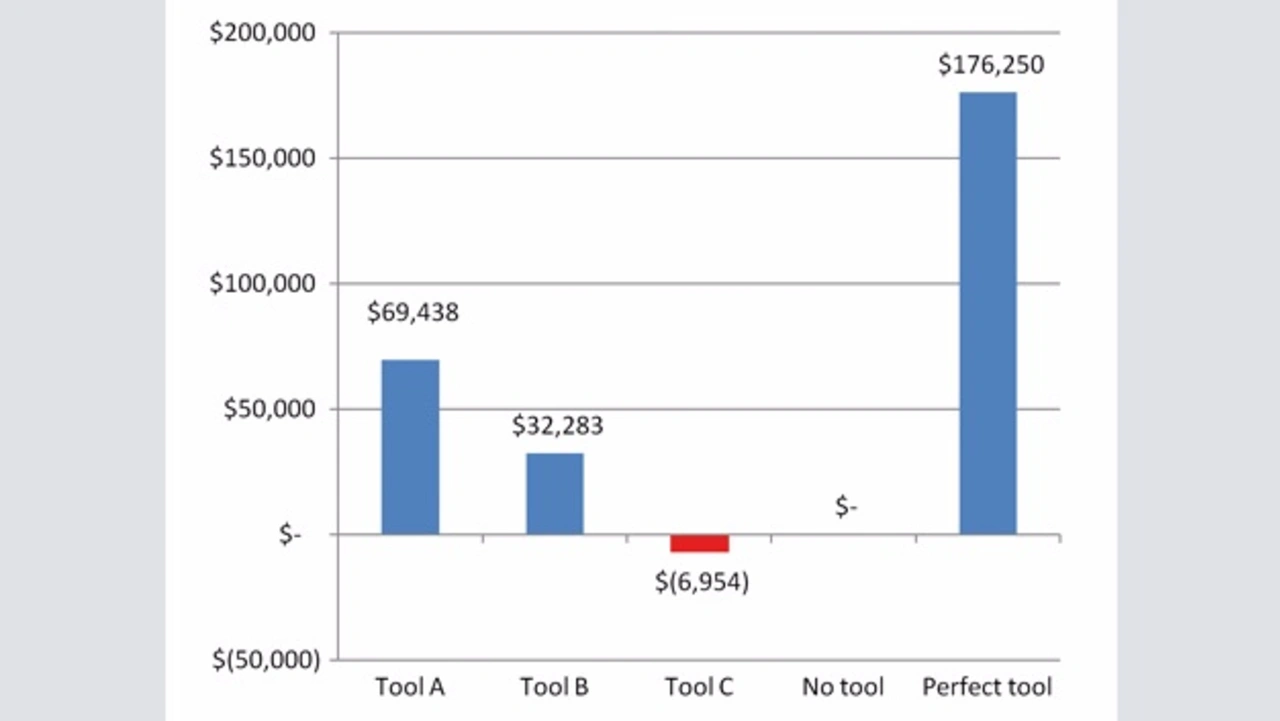
Um den Nutzen des Tools zu bewerten, eignet sich der Vergleich zwischen diesen Kosten und jenen aus dem Umgang mit entdeckten Fehlern, wenn kein Tool zum Einsatz gekommen wäre. Unter der Annahme des kubischen Modells zur Erkennung von True Positives zeigt Bild 3a und Bild 3b die Kostenaufschlüsselung und die Vorteile.
Wieder bietet das Tool, das eine vernünftige Balance zwischen Precision und Recall erzielt, den größten Nutzen. Tool A ist vorteilhafter, auch wenn es nur rund halb so viele echte Fehler wie Tool C gefunden hat, und obwohl es acht Mal mehr False Positives als Tool B berichtet. Interessant ist auch, dass Tool C knapp unter dem Break-Even-Point steht, auch wenn es den höchsten Recall erzielt.
Die jeweilige Reihenfolge der Tools ist relativ unabhängig von den tatsächlichen Werten bei Kosten und Wahrscheinlichkeit eines Zwischenfalls – vorausgesetzt, die Aufwendungen für einen Zwischenfall überschreiten die Ausgaben zur Behebung der vom Tool gefundenen Defekte. In einem solchen Extremfall ist die kosteneffektivste Strategie, kein Tool einzusetzen.
Dieses Modell bestätigt, dass der Vorteil des Einsatzes eines statischen Analysetools von dessen Fähigkeit abhängt, echte Fehler zu entdecken, die in der Folge als solche erkannt werden. Auch wenn die Sichtung der Warnungen Kosten verursacht, sind diese relativ niedrig verglichen mit denen eines Zwischenfalls. Somit ist die Effektivität eines Tools, z. B. seine Fähigkeit, echte Fehler zu entdecken, die als solche erkannt werden, eine gute Annäherung an seinen Gesamtnutzen. Zu beachten ist aber, dass dies Kenntnis über den Wert eines Recalls voraussetzt, der – wie erwähnt – schwer zu fassen ist.
Über den Autor:
Dr. Paul Anderson ist Vice President Engineering bei Grammatech.