Für den Entwickler unter der Lupe: eine Filter-Kategorie mit vielen Vorteilen
Rekursiv-Filter optimal entwickeln
Fortsetzung des Artikels von Teil 3
Filterrealisierung im Festkomma-Format
Hinsichtlich minimaler Kosten und eines geringen Leistungsverbrauchs stellt eine Implementierung im Festkomma- Format heute nach wie vor die günstigste Form der Realisierung dar und wird daher weitaus häufiger eingesetzt als eine Implementierung im Gleitkomma-Format. Hierbei kommen sowohl Realisierungen mit Hilfe von Standard-DSPs als auch Realisierungen als FPGA oder kundenspezifisches ASIC in Betracht.
Bei der Implementierung von rekursiven Filtern im Festkomma-Format ist allerdings zu beachten, dass diese sehr empfindlich gegenüber Wortlängenbegrenzungseffekten sein können. Dies gilt insbesondere auch im Vergleich zur Realisierung als FIRFilter (FIR: Finite Impulse Response). Es ist daher zwingend erforderlich, dass der Anwender einige zusätzliche Randbedingungen bei der Implementierung beachtet. Ansonsten kann es bei der Inbetriebnahme dieser Filter zu bösen Überraschungen kommen, im schlimmsten Fall ist das implementierte Filter völlig unbrauchbar.
Jobangebote+ passend zum Thema
Die Übertragungsfunktion eines rekursiven Digitalfilters lässt sich mit der Variablen z = ejω wie folgt beschreiben:

Hierfür kann eine direkte Realisierung angegeben werden, die sich allerdings als sehr empfindlich gegenüber einer Quantisierung der Koeffizienten erwiesen hat. Eine weitaus robustere Struktur ergibt sich durch eine Zerlegung der Übertragungsfunktion in Produktterme zweiter Ordnung und gegebenenfalls einen erster Ordnung:

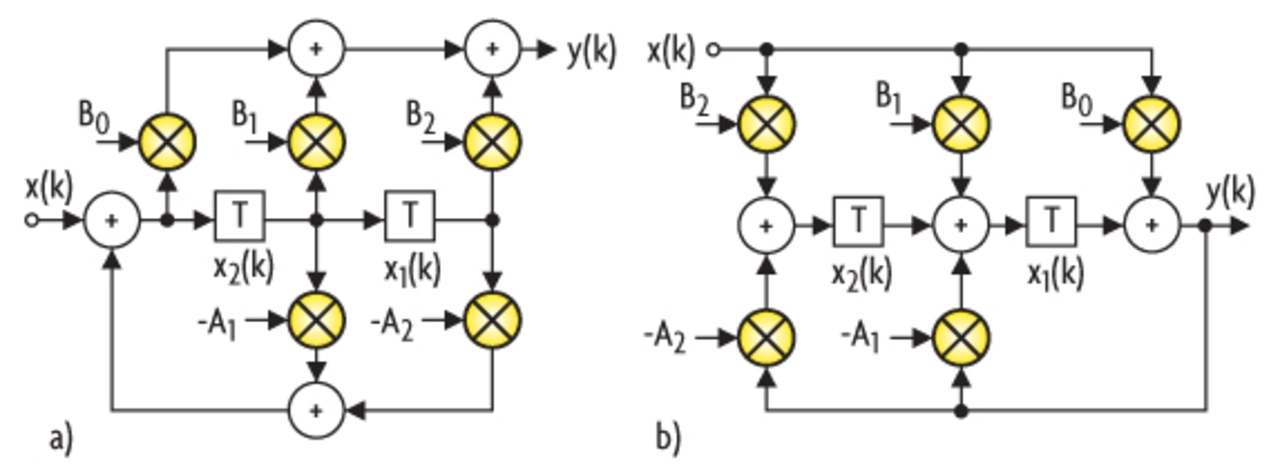
Eine Realisierung des Systems erfolgt entsprechend durch die Kaskadenschaltung von Blöcken zweiter Ordnung, für eine ungerade Filterordnung wird ein zusätzlicher Block erster Ordnung kaskadiert. Bild 2 zeigt zwei unterschiedliche Implementierungsmöglichkeiten für einen solchen Filterblock zweiter Ordnung, für dessen Übertragungsfunktion gilt:

Diese Anordnung aus kaskadierten Filterblöcken niedriger Ordnung hat sich als weitaus robuster hinsichtlich der Koeffizientenquantisierung erwiesen. Die weitere Optimierung der Filterstruktur kann unter Ausnutzung folgender Freiheitsgrade erfolgen:
- Zuordnung der Pole und Nullstellen zu den Produkttermen,
- Reihenfolge der Filterblöcke,
- Skalierung der Signale in den einzelnen Blöcken.
Darüber hinaus ist der Filterblock durch unterschiedliche Strukturen realisiertbar; man unterscheidet zwischen vier kanonischen Formen sowie den Direktformen I und II und deren transponierten Strukturen [1, 2]. Auch die Wahl der Struktur kann zur Optimierung ausgenutzt werden.
Die Auswahl der optimalen Struktur, die Zuordnung der Pole und Nullstellen zu den Produkttermen und deren Skalierung können mit Hilfe analytischer Methoden optimiert werden. Auf Grund der vielen Möglichkeiten, die sich hierbei ergeben, kann dies jedoch sehr zeitaufwendig werden. In der Praxis hat sich daher ein Vorgehen bewährt, das mit Hilfe einfacher Regeln sehr schnell zu einer annähernd optimalen Lösung führt. Hierbei werden jeweils zwei konjugiert komplexe Pole mit den jeweils zwei zu diesen am dichtesten liegenden, konjugiert komplexen Nullstellen zu einem Term zweiter Ordnung kombiniert. Dadurch lassen sich hohe Signalamplituden und damit Übersteuerungen bei den Frequenzen vermeiden, die den Polen entsprechen. Bei der Anordnung der Filterblöcke wählt man entweder die gleiche oder die entgegengesetzte Reihenfolge, in der man die Glieder zweiter Ordnung zusammengefasst hat. Die Aufteilung in Filterblöcke zweiter Ordnung nach diesen einfachen Regeln ist inzwischen auch in einigen Filterentwurfsprogrammen implementiert, so dass der Entwickler auch an dieser Stelle entlastet wird.
Der verbleibende Einfluss der Koeffizientenquantisierung auf die Übertragungsfunktion kann beim Filterentwurf berücksichtigt werden. Hierbei ist insbesondere zu beachten, dass die Pole auch nach der Quantisierung nicht außerhalb des Einheitskreises liegen, da die Schaltung ansonsten instabil wird.
Darüber hinaus sind die Wortlängenbegrenzungseffekte zu betrachten, die durch die arithmetischen Operationen während der Filterberechnung auftreten. Sie können die Eigenschaften eines rekursiven Filters ganz erheblich beeinflussen. Hierzu gehören insbesondere die Fehler durch Überläufe und durch Runden. Hierbei stellen Überläufe die kritischere Fehlerursache dar, da sich ein System durch diese nichtlinear verhält und große Fehler entstehen können, die sogar zu Instabilitäten in Form von Grenzzyklen führen können.
Grenzzyklen in rekursiven Filtern
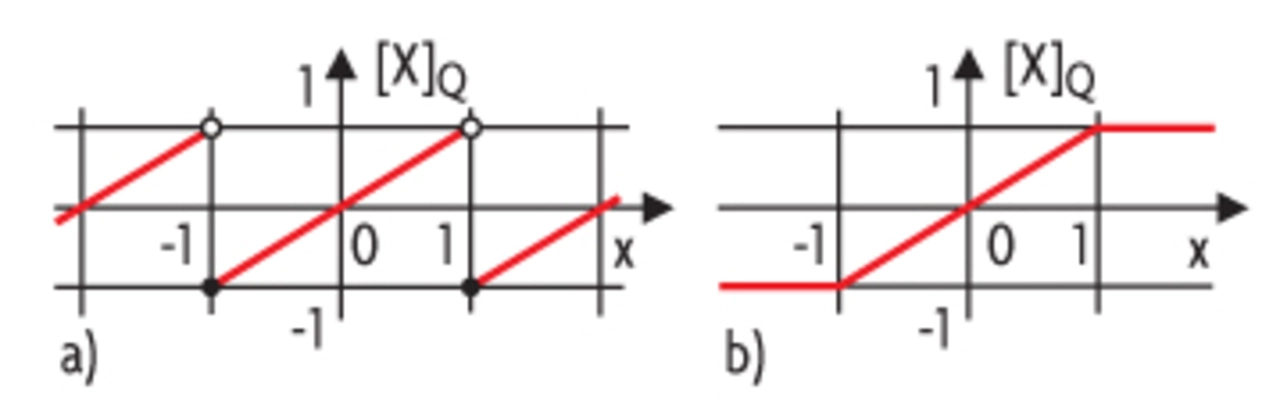
Bei der Addition im Zweierkomplement kann es zu einem Überlauf kommen. Das Überlaufverhalten wird durch die Überlaufkennlinie in Bild 3 charakterisiert. Die Addition wird im Falle des Überlaufs zu einer nichtlinearen Operation. Der Zweierkomplement- Überlauf kann sich im ungünstigen Fall in Form von großen Grenzzyklen auswirken, so dass das Filter instabil und dadurch unbrauchbar wird. Abhilfe schafft hier die Sättigung, durch die ZweierkomplementÜberläufe vermieden werden. Die entsprechende Kennlinie ist in Bild 3b wiedergegeben. In diesem Fall wird bei einem positiven oder negativen Überlauf die kleinste oder größte darstellbare Zahl ausgegeben. Instabilitäten lassen sich dadurch vermeiden, aber das Signal wird nach wie vor verfälscht. Eine bessere Abhilfemaßnahme stellt daher eine geeignete Skalierung der Eingangssignale der einzelnen Filterblöcke dar, so dass es nicht zu Überläufen kommen kann. Hierzu wird das Eingangssignal des Filterblocks mit einem multiplikativen Faktor α multipliziert, so dass die Verstärkung vom Eingang bis zu den kritischen Knoten kleiner oder gleich 1 ist. Der Skalierungsfaktor wird hierbei auch in Abhängigkeit von der Form des zu filternden Signals bestimmt. Handelt es sich typischerweise um ein schmalbandiges Signal, so verwendet man die L∞-Norm, die sich aus dem Maximalwert des Signals am kritischen Punkt ergibt. Der Skalierungsfaktor α1 ergibt sich aus der Übertragungsfunktion A(z) vom Eingang zu diesem Knoten gemäß folgender Beziehung:

Für breitbandige Signale verwendet man dagegen die L2-Norm, die sich aus der Leistung des Signals am kritischen Knoten ergibt:

Hierbei gilt α1 ≥ α2. Damit die Skalierung durch eine einfache Shift-Operation realisiert werden kann, wählt man für die Faktoren bevorzugt Werte, die durch Potenzen von 2 ausgedrückt werden können. Darüber hinaus besteht die Möglichkeit, den Skalierungsfaktor mit den Koeffizienten der Strukturen in Bild 2 zu kombinieren. Am Ausgang des Filterblocks muss das Signal mit dem Reziprokwert des Skalierungsfaktors multipliziert werden. Da das Eingangssignal durch die Skalierung verkleinert wird, verschlechtert sich allerdings durch die Skalierung das Signal/ Rausch-Verhältnis des Ausgangssignals. Außerdem muss in Zusammenhang mit der Skalierung die optimale Reihenfolge der Filterblöcke betrachtet werden, da diese sehr unterschiedliche Verstärkungsfaktoren aufweisen können. Ziel hierbei ist es, Überläufe zu vermeiden und gleichzeitig das Rundungsrauschen zu minimieren.
Bei der Multiplikation im Zweierkomplement kommt es zwar nicht zu einem Überlauf, allerdings erhöht sich im Allgemeinen die Anzahl der benötigten Binärstellen. Das Produkt von zwei Zahlen mit n signifikanten Stellen benötigt 2n – 1 Bits für seine exakte Darstellung.
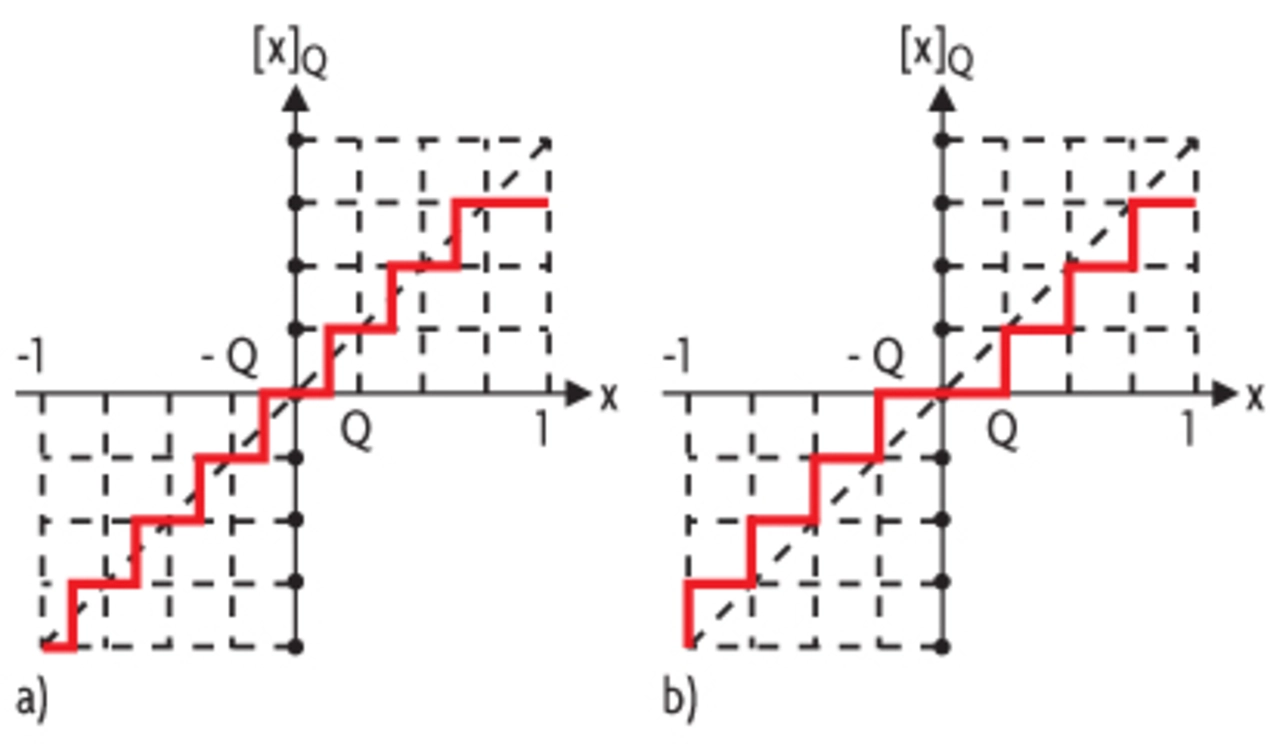
Wird das Produkt nicht mit der vollen Wortlänge weiterverarbeitet, so wird auch die Multiplikation zu einer nichtlinearen Operation. Spätestens nach der Addition wird eine Wortlängenverkürzung vorgenommen, wenn die Zustandsvariablen x1(k) und x2(k) in der ursprünglichen Wortbreite abgespeichert werden. Zwei gängige Methoden zur Wortlängenbegrenzung sind das Runden und das Betragsschneiden, die entsprechenden Kennlinien sind in Bild 4 dargestellt. Es wird deutlich, dass beim Betragsschneiden der Betrag der Zahl durch die Quantisierung nicht zunehmen kann.
Die Quantisierung durch Runden wirkt sich dagegen beim Aufrunden wie eine zusätzliche Quelle aus, die dem System Energie zuführt. Durch das Runden können daher kleine Grenzzyklen entstehen, die in Form eines periodischen Signals am Systemausgang erscheinen. Dieses Signal – mit einer Amplitude in der Größenordnung von wenigen Quantisierungseinheiten – bleibt weiter bestehen, auch wenn das Eingangssignal längst den Wert Null angenommen hat. Beim Betragsschneiden wird dem System dagegen keine zusätzliche Energie zugeführt. Kleine Grenzzyklen lassen sich also auf Kosten der Genauigkeit vermeiden.
- Rekursiv-Filter optimal entwickeln
- Literatur
- Rauschen eines Filterblocks zweiter Ordnung
- Filterrealisierung im Festkomma-Format