Für den Entwickler unter der Lupe: eine Filter-Kategorie mit vielen Vorteilen
Rekursiv-Filter optimal entwickeln
Fortsetzung des Artikels von Teil 2
Rauschen eines Filterblocks zweiter Ordnung
In den meisten Fällen können die Fehler durch die Wortlängenverkürzung in guter Näherung als unkorreliertes, additives Rauschsignal modelliert werden. Entsprechend gilt für die Rauschleistung Nn:

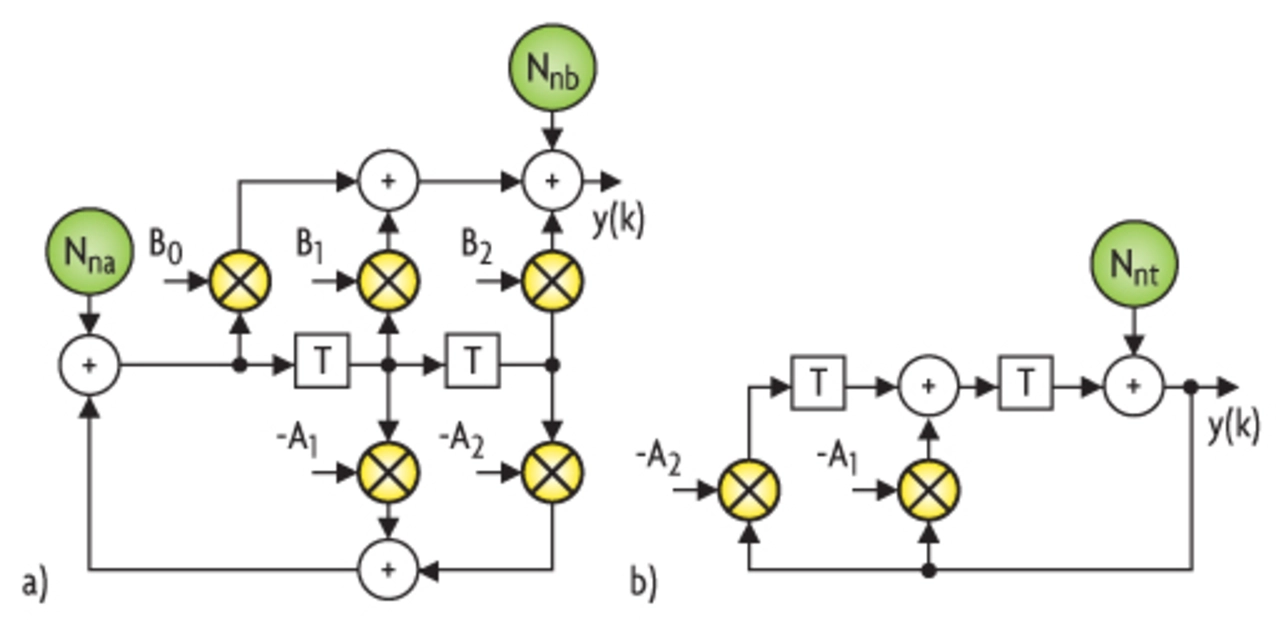
Hierbei entspricht Q der Quantisierungseinheit oder dem LSB (Least Significant Bit). In einem Block zweiter Ordnung finden bis zu fünf Multiplikationen statt. Geht man davon aus, dass hinter jedem Multiplizierer eine Wortlängenbegrenzung stattfindet, so kann man an der entsprechenden Stelle im Ersatzschaltbild eine Rauschquelle Nn einfügen. zeigt die entsprechende Ersatzschaltung für die Struktur in Bild 2a, wobei die Rauschquellen hinter den Multiplizierern mit den Koeffizienten Ai zur Rauschquelle Nna und die der Bi zur Rauschquelle Nnb zusammengefasst wurden. Es gilt:

Die Integerzahlen Ka und Kb geben jeweils die Anzahl der Wortbegrenzungen hinter den Koeffizienten Ai und Bi an. Erfolgt hinter jedem der fünf Multiplizierer eine Wortbegrenzung so sind Ka = 2 und Kb = 3.
Jobangebote+ passend zum Thema
Das Rauschsignal am Systemausgang wird als inneres Rauschen bezeichnet. Für das linearisierte Modell in Bild 5a kann die Rauschleistung Nt am Systemausgang mit Hilfe folgender Beziehung bestimmt werden:

Das Rauschen der Quelle Nna wird also mit der gleichen Übertragungsfunktion H(ejω) wie das Signal gefiltert, während Nnb ohne Filterung an den Ausgang weitergegeben wird.
Völlig anders hinsichtlich des Rauschens verhält sich dagegen der Filterblock in Bild 2b, der die gleiche Übertragungsfunktion für das Signal aufweist. Das linearisierte Ersatzschaltbild für das Rundungsrauschen ist in Bild 5b wiedergegeben. Zur Bestimmung der Rauschleistung am Ausgang können die Zweige mit den Koeffizienten Bi entfallen, da diese keinen Einfluss auf das Rauschen am Ausgang haben. Dies wurde entsprechend in Bild 5b berücksichtigt. Für die Rauschleistung Nt am Systemausgang gilt jetzt:

Der Faktor K berücksichtigt wieder, dass mehrere Rauschquellen im System vorhanden sind, die zu einer Rauschquelle Nnt zusammengefasst wurden. A(z) entspricht dem Nennerpolynom der Übertragungfunktion. Findet in dem Block in Bild 2b eine Wortlängenbegrenzung jeweils vor dem Abspeichern der Zustandsvariablen statt, so ist K = 2. Erfolgt eine Wortlängenbegrenzung hinter jedem der fünf Multiplizierer, so ergibt sich ein Wert von K = 5. Das Integral in Gl. 9 lässt sich explizit berechnen, es gilt [2, 4]:

In Abhängigkeit der Koeffizientenwerte Ai, die die Polstellen der Übertragungsfunktion bestimmen, kann das Rundungsrauschen durch die Rückkopplung im System jetzt also eine sehr große Verstärkung erfahren. Insbesondere schmalbandige Filter sind diesbezüglich ungünstig, da bei ihnen das Rauschen eine große Verstärkung erfährt. Welche der beiden Filterstrukturen allerdings die günstigere hinsichtlich des Rauschens ist, lässt sich nicht von vornherein sagen und hängt insbesondere von den Koeffizientenwerten ab.
Brücken-Wellendigitalfilter, eine gute Wahl für rekursive Filter
Wellendigitalfilter [5, 6] haben eine Reihe von Vorteilen gegenüber den bisher betrachteten, rekursiven Filterstrukturen. Insbesondere weisen sie hervorragende Stabilitätseigenschaften auf. Dies gilt selbst unter nichtlinearen Betriebsbedingungen, zum Bei spiel hervorgerufen durch Runden oder Überläufe. Darüber hinaus ist der Dynamikbereich bei vorgegebener Wortlänge deutlich besser als bei den zuvor vorgestellten Strukturen. Dies ist insbesondere darauf zurückzuführen, dass sich Wellendigitalfilter bei geeignetem Entwurf so verhalten wie das passive Referenzfilter, von dem sie abgeleitet wurden.
Für die Realisierung von Wellendigitalfiltern existiert eine Fülle von Strukturen. Als besonders vorteilhaft haben sich Brücken-Wellendigitalfilter erwiesen [5], die zu Implementierungen mit geringem Realisierungsaufwand führen. Die Koeffizienten dieser Filter lassen sich sehr einfach mit Hilfe expliziter Formeln berechnen [6]. Entsprechende Software- Werkzeuge wurden zur Berechnung der Filterkoeffizienten entwickelt und können für den Entwurf genutzt werden. Entwurfsprogramme auf der Basis von MATLAB wurden auch an der Universität Wuppertal erstellt und werden am Lehrstuhl für Nachrichtentechnik intensiv für den Entwurf von optimierten Wellendigitalfiltern eingesetzt.
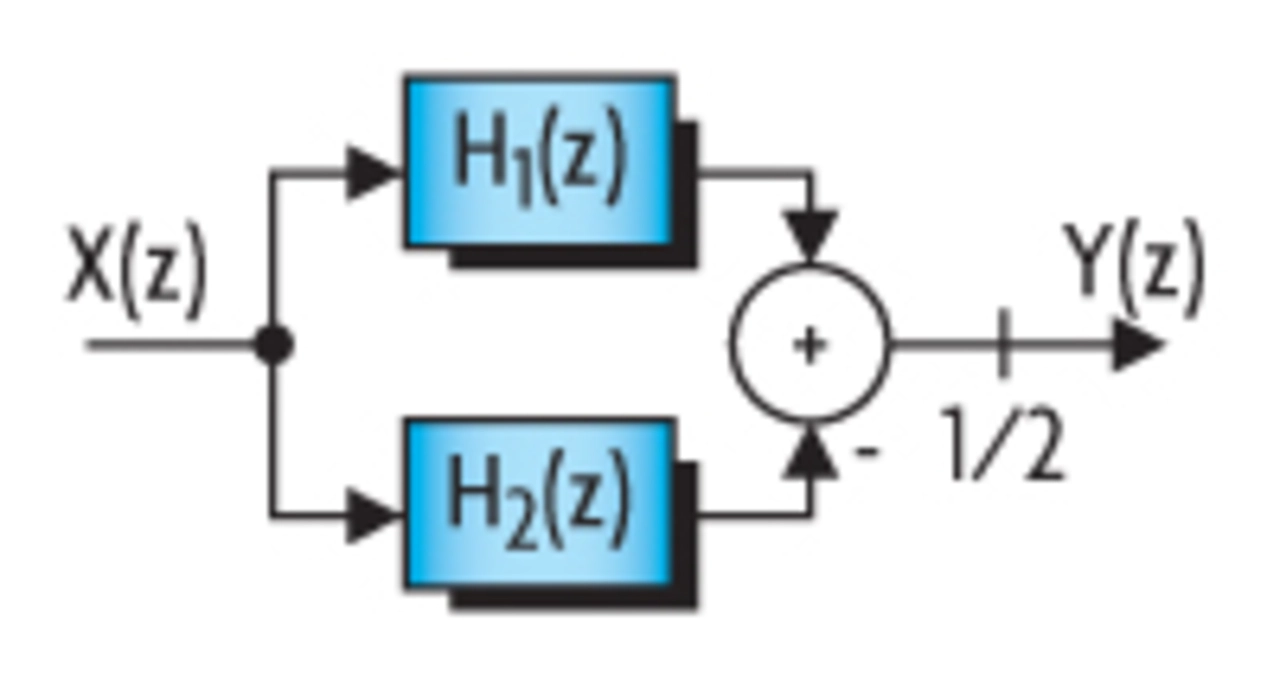
Brücken-Wellendigitalfilter setzen sich aus zwei Brückenzweigen zusammen, wie das Blockdiagramm in Bild 6 zeigt. Die beiden Brückenzweige lassen sich durch die Kaskadierung einfacher Allpässe zweiter und gegebenenfalls einem erster Ordnung realisieren. Die Übertragungsfunktion eines Brücken- Wellendigitalfilters kann mit Hilfe der Übertragungsfunktionen H1(z) und H2(z) der beiden Allpasszweige wie folgt beschrieben werden [5, 6]:

Für die Übertragungsfunktion eines Allpasses erster Ordnung gilt:

Der Koeffizient C liegt im Bereich –1 ≤ C ≤ +1. Entsprechend gilt für die Übertragungsfunktion der Zelle zweiter Ordnung mit den Koeffizienten C1 und C2:

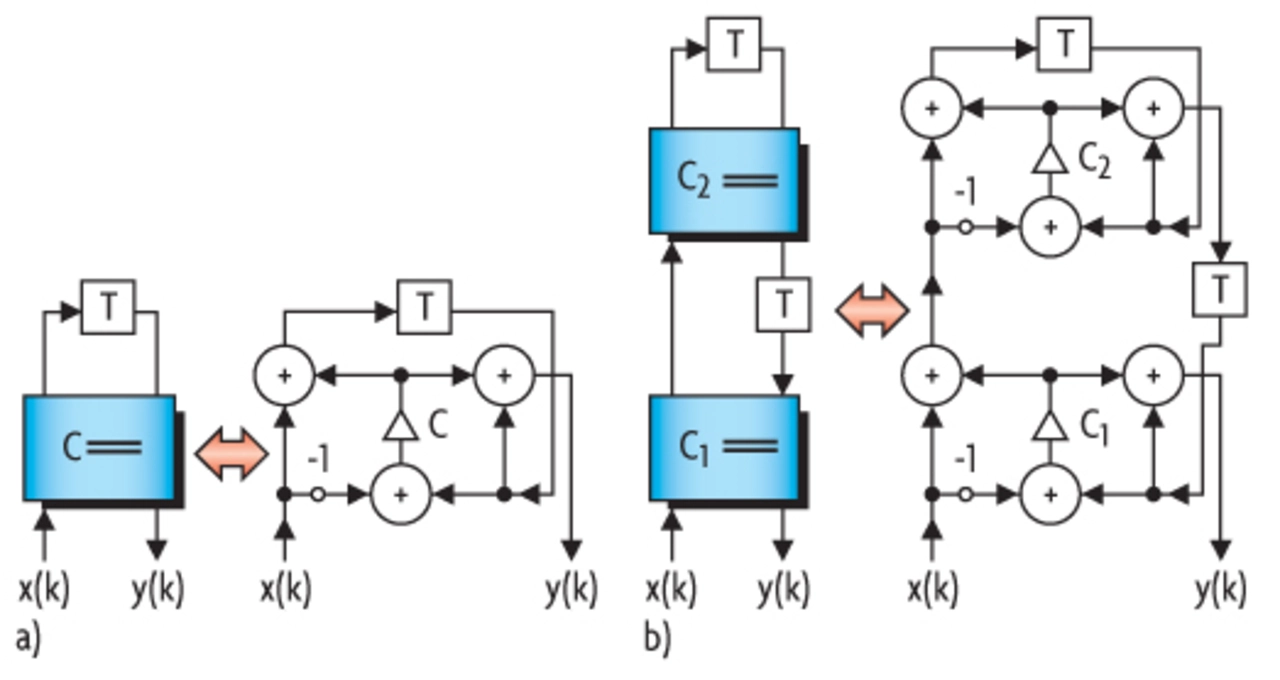
Zwei mögliche Realisierungen der Allpassglieder sind in Bild 7 dargestellt. Sie setzen sich aus Verzögerungsgliedern und so genannten Adaptoren [5, 6] zusammen. Für die Realisierung eines Adaptors sind drei Additionen und eine Multiplikation erforderlich. Eine Zelle erster Ordnung besteht aus einem Adaptor und einem Verzögerungsglied. Eine Zelle zweiter Ordnung kann entsprechend mit zwei Adaptoren und zwei Verzögerungsgliedern realisiert werden, so dass hierfür sechs Additionen und zwei Multiplikationen ausgeführt werden müssen.
Darüber hinaus gibt es weitere Realisierungsmöglichkeiten für die Adaptoren, die in Abhängigkeit vom Koeffizientenwert zu einer besseren Skalierung führen. Die Strukturen sind in der Literatur beschrieben [6] und können für eine Optimierung der Skalierung ausgenutzt werden.
Brückenfiltern ergibt sich daraus, dass die Sperrdämpfung durch einen Kompensationseffekt zwischen den beiden Allpasszweigen erzeugt wird. Dadurch ist die Empfindlichkeit im Sperrbereich bezüglich einer Koeffizientenquantisierung relativ groß. Durch eine diskrete Optimierung der Koeffizientenwerte lassen sich jedoch in den meisten Fällen sehr günstige Werte bestimmen.
Bei vielen Anwendungen können die Koeffizientenwerte sogar so optimiert werden, dass sie nur wenige Stellen ungleich Null aufweisen. Dann lässt sich die Multiplikation ausschließlich durch " Shift-and-Add" - Operationen realisieren. Die Multiplizierer können daher in vielen Fällen entfallen, wodurch sich der erforderliche Hardware-Aufwand ganz erheblich reduzieren kann. Dies ist für eine Realisierung als ASIC oder FPGA sehr vorteilhaft.
- Rekursiv-Filter optimal entwickeln
- Literatur
- Rauschen eines Filterblocks zweiter Ordnung
- Filterrealisierung im Festkomma-Format